Dot Product In Physics: What Is The Physical Meaning of It?

The dot product is a mathematical operation between two vectors that produces a scalar (number) as a result. It is also commonly used in physics, but what actually is the physical meaning of the dot product?

The physical meaning of the dot product is that it represents how much of any two vector quantities overlap. For example, the dot product between force and displacement describes the amount of force in the direction in which the position changes and this amounts to the work done by that force.

In this article, we’ll be discussing this in a lot more detail as well as looking at some examples of how dot products are used in physics.

We’ll also discuss some more general notions of dot products, which are useful for relativity and quantum mechanics, among other things.

If you’re interested in learning physics more deeply, you may enjoy my Advanced Math For Physics: A Complete Self-Study Course – it’s the perfect place to get started learning more advanced physics and math, as it begins from the very fundamentals.

Significance of The Dot Product In Physics: Intuitive Explanation + Examples

In an intuitive sense, the dot product is a measure of how much two vectors are aligned. So, if we have two vectors, u and v, the dot product between these two would give the length of the vector v along the vector u, or if you will, the projection of v along u.

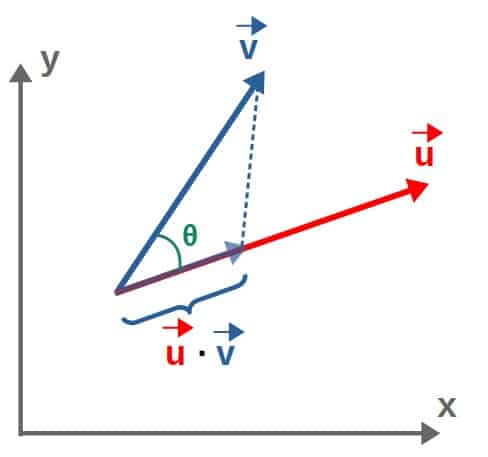
If we know the angle between the two vectors (θ in the above picture), the dot product can be calculated by the following formula:

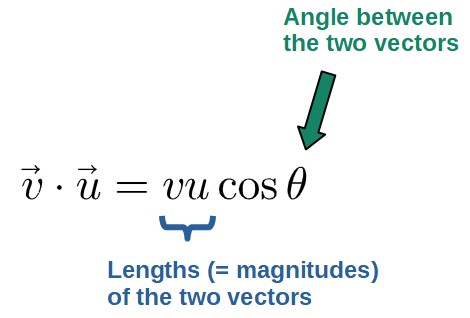
An interesting way to interpret this cos(θ) -factor is that it describes a kind of “percentage of alignment” between the two vectors; if cos(θ)=1, the vectors are fully aligned (since θ=0°) and if cos(θ)=0 (meaning θ=90°), the vectors don’t align at all. Moreover, something like cos(θ)=0.97 (θ≈15°) would correspond to the vectors being “almost aligned”.

The dot product can also be calculated in terms of the components of these vectors by using the following formula:

\vec{v}\cdot\vec{u}=\sum_i^{ }v_iu_i=v_1u_1+v_2u_2+v_3u_3

In general, this formula is valid for any number of dimensions, but here I’ve only written in in three dimensions.

Now, what’s the significance of all of this to physics? Well, many physical quantities are described by vectors (for example, velocity and forces), so it only makes sense that the dot product also has some physical significance.

In particular, the same geometric picture applies in physics as well; the dot product gives the length of one vector along another vector, but now, vectors represent something physical.

The best way to explain the physics of this is through an example. Namely, the dot product between a displacement vector and a force vector, which could be described as “the change in position (displacement) in the direction of the force”.

This quantity gives the work done by the force, which is essentially the change in energy caused by this force. More precisely, the work done along some path is actually given by a line integral of this dot product, which I explain in this article.

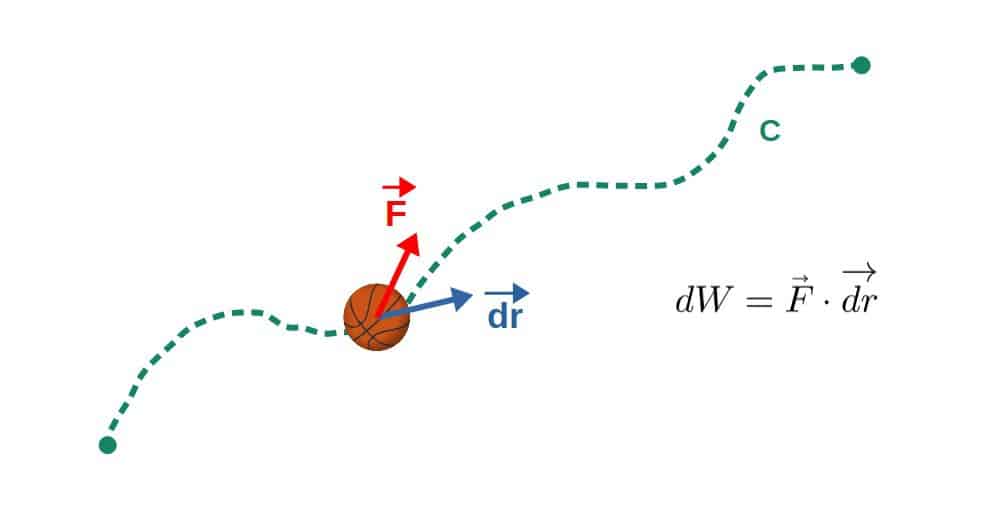
Hopefully this is enough motivation to establish why dot products are indeed useful in physics. There are thousands of different applications for the dot product ranging from basic mechanics to electromagnetism and even to graphic design and animations.

A nice explanation of this can be found in the video below:

Now, in higher-level physics, dot products are also useful but for slightly different reasons than the elementary geometric interpretation given above.

Namely, the dot product is useful because it has some nice mathematical properties that can be generalized very well to more abstract and more advanced areas of physics.

For example, the usual way to deal with mechanics problems is by using Newton’s laws, which are essentially vector equations.

However, an alternative way is to use only energies (which are scalars) and this is done in a formulation of mechanics called Lagrangian mechanics. I actually have a whole introductory article discussing Lagrangian mechanics, which you can find here.

Lagrangian mechanics is a highly elegant formulation of mechanics and part of that elegance comes from the fact that energy is a scalar quantity, which is partly due to the mathematical properties of the dot product.

This is because kinetic energy is a scalar since it involves only a dot product of velocities (I explain this and much more about the kinetic energy formula in this article).

This directly brings us to one of the defining properties of the dot product; it is a mathematical operation that gives a scalar as a result.

This is particularly important since scalars are invariant quantities (I’ll explain this later) that have a lot of use in, for example, special and general relativity.

For our purposes, the main properties of the dot product are:

• The dot product is a scalar.
• The dot product is commutative (though this is not true for operators anymore; this fact is actually part of where the richness of quantum mechanics comes from).
• The dot product defines a notion of orthogonality (if the dot product between two quantities is zero).

We’ll talk about these properties more later, but it’s worth noting that while these may seem obvious when only looked at from the lens of this “basic” definition of the dot product, they really are what defines the dot product itself.

This is why these properties are important if we wish to generalize the notion of the dot product to more complicated situations, such as curved spacetime in general relativity. This is what we’ll talk about next.

Dot Product In Special And General Relativity

In general relativity, gravity and the motion of objects under the influence of gravity, is explained by spacetime (so both space and time) itself being curved, which results in the effects of gravity and gravitational acceleration.

Everything we’re interested in in general relativity, essentially takes place in curved spacetime. You could therefore think of the mathematics of general relativity as simply ordinary math but done in a “curved geometry”.

Now, the difficulty of this comes from the fact that if we’re dealing with some arbitrarily curved spaces, how can there be any kind of a universal notion of a dot product? The answer is that there cannot, at least not in the way we’re used to.

Really, the problem comes from the fact that in a curved spacetime, the basis vectors (which are used to express components of vectors) are not constant and may vary from place to place.

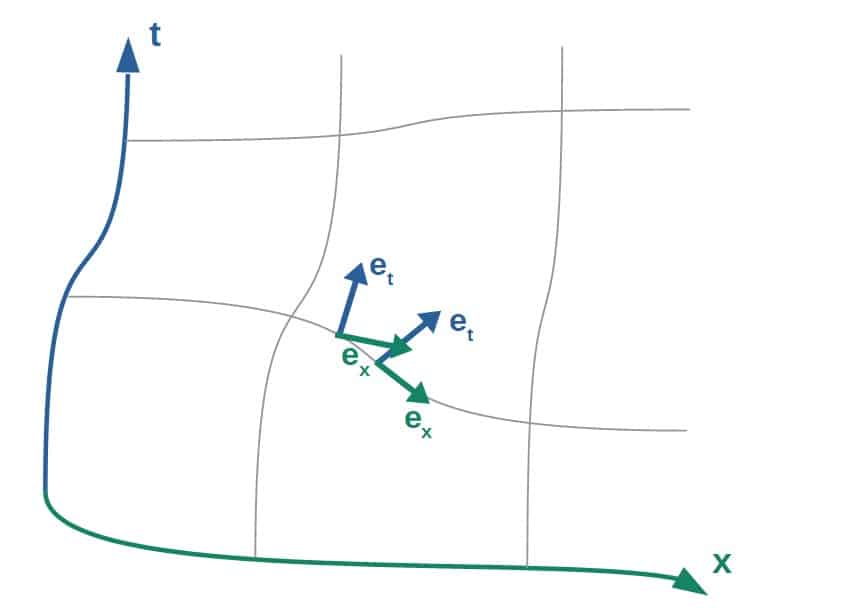
If the basis vectors are not constant, we can’t define the dot product as simply just the sum of the products of components:

\vec{v}\cdot\vec{u}\ne v_1u_1+v_2u_2+v_3u_3

Instead, we use an object called the metric tensor, which you can think of as adding a “correction factor” to each term in this dot product to account for the fact that the basis vectors may be different from place to place:

\vec{v}\cdot\vec{u}=g_{11}v_1u_1+g_{22}v_2u_2+g_{33}v_3u_3

Note that these metric components (the g’s here) are actually components of a two-index tensor rather than vector components. This is why they have two indices. Moreover, the metric is generally a function that can also vary from place to place like the basis vectors.

More generally, the dot product can be written as:

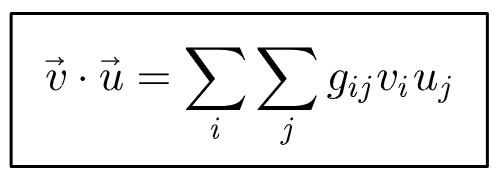
Instead of the usual dot product formula, we now have a double sum, which CAN actually have cross-terms involving products of the vector components such as v₁u₂. This is indeed possible if the basis vectors are not constant, but not in the typical Cartesian (x,y,z) coordinate system.

This is the formula for the dot product between two vectors in any arbitrary coordinate system or space (although there are some mathematical restrictions, which we won’t get into now).

Now, the metric for any given spacetime is typically calculated from the Einstein field equations of general relativity, which specifies the geometry of that spacetime by its energy and momentum content. This is the usual way of calculating different spacetime metrics in general relativity.

By using the metric, it’s possible to derive all kinds of physical results from general relativity, such as time dilation near a black hole. I discuss this and its geometric as well as physical interpretations in detail in this article.

Now, the bottom line with all of this is that it is possible to define a notion of the dot product in curved spaces and coordinate systems by using a metric tensor.

The physical meaning of this is more or less the same still; the dot product is a measure of how much two vectors align, although this is a bit more difficult to picture if we’re dealing with a curved geometry.

In any case, the mathematics of curved spaces (and differential geometry in general) is fascinating and holds so many interesting concepts which have applications in so many areas of physics too.

If you want to learn more about these, I recommend my article on the Christoffel symbols, one of the central mathematical tools used in general relativity, as well as my article on the Ricci tensor, which has an interesting physical meaning having to do with gravitational tides.

Dot Product In Quantum Mechanics (The Inner Product)

The dot product in quantum mechanics is quite a bit more abstract than any of the notions we talked about before.

Besides, it usually doesn’t even go by the name if a dot product, but rather the inner product (to be precise, the inner product actually refers to a more general “class” of mathematical operations than the dot product).

The inner product between two vectors is denoted by “sandwiching” together a bra vector (the thing on the left) and a ket vector (the thing on the right):

\left\langle v|u\right\rangle

Now, this is equivalent to a typical dot product, except that in quantum mechanics, we’re usually dealing with complex numbers. So, this inner product is actually:

\left\langle v|u\right\rangle=v_1^{\ast}u_1+v_2^{\ast}u_2+v_3^{\ast}u_3+...

Here, the star denoted the complex conjugate of the components of v. Note that this is pretty much the same as the dot product for “ordinary” vectors, except generalized to complex numbers.

Now, these bra’s and ket’s (the v and u with these weird brackets around them) are indeed vectors. However, they are not the typical vectors in 3D space, but rather they are abstract state vectors in a complex vector space.

The physical meaning of them is that they represent quantum states of a system. Now, what this practically means will depend on the particular state vector. For example, we could have a state vector that represents a particle with some momentum and this would be a perfectly valid quantum state.

The dot product (or inner product) also has pretty much the same meaning, except that it is now a mathematical operation in an abstract vector space, so we cannot picture it geometrically.

An important application of these inner products in quantum mechanics is for basis states. These are analogous to basis vectors, but again they are abstract complex vectors. Basis states are defined by the following inner products:

\left\langle\Psi_1|\Psi_1\right\rangle=1

The first equation here means that our basis state is normalized (its “square” is 1). This allows for a probabilistic interpretation in quantum mechanics.

\left\langle\Psi_1|\Psi_2\right\rangle=0

The inner product here being equal to zero means that our two states are orthogonal. In quantum mechanics, this corresponds to these basis vectors representing distinct quantum states, for example, states of definite momenta (as opposed to a superposition of different momenta).

Now, these define a “basis” in this abstract vector space and we can indeed represent any possible quantum mechanical state by using these basis states (this is analogous to how any vector can be expressed in terms of basis vectors).