Why Time Slows Down Near a Black Hole: The Physics Explained
Black holes are some of the most intriguing, yet not very well-understood objects in the universe, which are best described by Einstein’s theory of general relativity.
One of the more interesting predictions of the theory is that even time will slow down near a black hole. But why, exactly?
Time slows down near a black hole due to the extremely strong gravitational field of the black hole. According to the theory of general relativity, this phenomenon is due to the gravity of the black hole curving spacetime in a way that affects all measurements of time and space near the black hole.
In this article, we’ll be discussing all about this slowing down of time -thing in great detail (namely the interesting geometry behind it) as well as looking at some consequences of this phenomenon (such as how it affects aging).
We’ll also look at some concrete examples of how much time actually slows down near a black hole as well as how different properties of black holes affect this (such as electric charge and spin).
In case you’d want an ad-free PDF version of this article (an my other general relativity articles), you’ll find it here, available as part of my full General Relativity Bundle.
Table of Contents
Gravitational Time Dilation Explained
If you’ve ever heard of general relativity or black holes before, you’ve probably also heard about the phenomenon called gravitational time dilation.
This is the effect a gravitational field has on the passing of time around it, namely that a clock will “tick” slower near, for example, a black hole than it would far away from the black hole.
The real question is, however, why such a phenomenon actually occurs and the answer is quite subtle but has a nice geometric explanation.
But, we need to first discuss the underlying ideas behind this geometric explanation.
The Geometry of Spacetime According To General Relativity
In general relativity, we model everything through a concept called spacetime. Essentially, this means that both space and time are “combined” together into a 4-dimensional geometry known as a manifold.
The effects of gravity are then modeled by the curvature of this spacetime manifold. If you wish to understand the underlying ideas behind this, I recommend reading this introduction to general relativity.
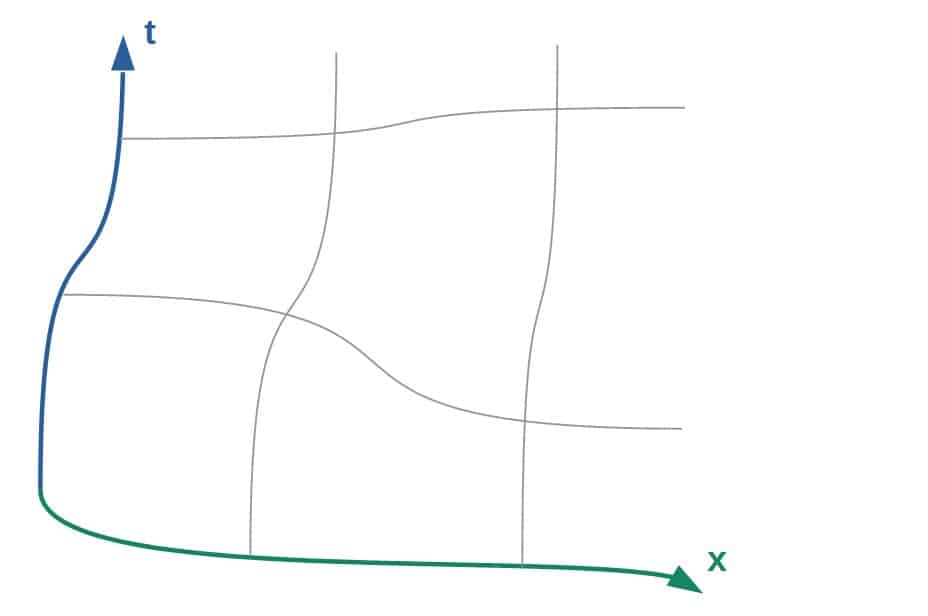
Anyway, if we wish to actually describe a point (these are called events) on a curved spacetime manifold, we need coordinates (one time coordinate and three space coordinates) or a coordinate system.
In a coordinate system, there are always basis vectors, which are used to generally describe any vector and its components in that system.
However, if the spacetime and thus, the coordinate system is curved (such as in a gravitational field in general relativity), these basis vectors are going to vary from point to point, which means their length and direction aren’t constant anymore.
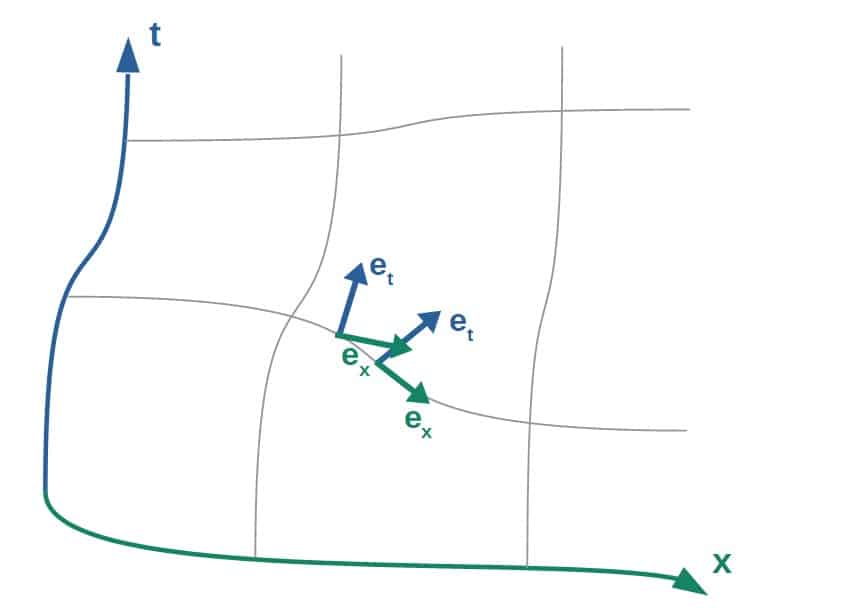
We describe how these basis vectors are different from point to point by using a metric tensor, which is essentially just a function that allows us to define a notion of length on any curved manifold.
The components of this metric tensor (at any point) are defined as the dot product between basis vectors:
g_{\mu\nu}=\vec e_{\mu}\cdot \vec e_{\nu}Since the dot product is a measure of how much two vectors are “aligned”, this means that the metric tensor measures the alignment of basis vectors at any given point. Also, more importantly for our discussion, the metric gives a measure of the lengths of basis vectors at a point.
Recommendation: To learn more about the metric tensor and what it actually describes geometrically, I highly recommend reading this article – either now, or after you’re done with this one.
Now, the changes of these basis vectors from point to point also have direct physical implications.
Namely, this means that measurements of physical quantities that are described by these spacetime coordinates (so time intervals and lengths) are going to differ from point to point.
We’ll discuss this (and most importantly how this can help us understand time dilation near a black hole) in the next section.
The Geometric Explanation Behind Gravitational Time Dilation
For our discussion regarding black holes, the curved spacetime geometry near a spherical black hole is such that the basis vectors in the time direction get shorter as one moves closer to the black hole (more on this down below).
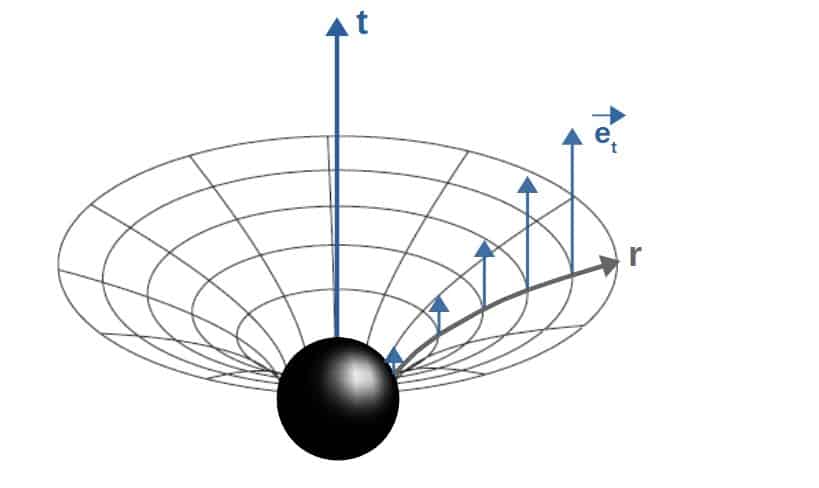
You can sort of picture this geometrically as the time dimension getting “squeezed” as one moves radially towards the black hole. This then results in the effect we call gravitational time dilation.
All of this is described by the usual metric from general relativity called the Schwarzschild metric. This is the metric describing spacetime (and gravity) around a spherically symmetric massive body.
The geometry of these basis vectors can be understood quite easily. Now, to really understand the mathematics here, you may need a little bit of an understanding of general relativity first. For that, I’d recommend checking out this step-by-step guide on self-studying general relativity.
Anyway, to describe what happens to the basis vectors in the time direction, we need the gtt-component of the Schwarzschild metric, which is defined as follows:
g_{tt}=-\left(1-\frac{r_s}{r}\right)Here, rs is a parameter known as the Schwarzschild radius and r is the radial coordinate (basically the distance from the center of the black hole).
On the other hand, the gtt-component of the metric can also be defined as the dot product between the et-basis vectors:
g_{tt}=\vec{e}_t\cdot\vec{e}_tThis gives a nice expression for the length of the et-basis vector through the metric. As a technical detail, the length (squared) of a basis vector is given by the absolute value of the metric component (since the metric components can be negative):
\left|g_{tt}\right|=\left|\vec{e}_t\right|^2\ \ \Rightarrow\ \ \left|\vec{e}_t\right|=\sqrt{\left|g_{tt}\right|}This absolute value sign denoted the length of the et-basis vector, which is the dot product between the et-basis vector with itself. This is, of course, just the metric component gtt, however, the “true length” of the basis vector requires taking the absolute value, which is really just a technical detail.
From this and the one equation above, we get a formula for the length of the et-basis vector as a function of the coordinate r by inserting the gtt-component of the Schwarzschild metric into this (note that due to the absolute value, the negative sign changes to a positive since the gtt-component of the metric is generally negative):
\left|\vec{e}_t\right|=\sqrt{1-\frac{r_s}{r}}From this, we can see that as r gets smaller (getting closer to the black hole), the length of the et-basis vector gets shorter.
At the point r=rs (this is the event horizon of the black hole), the length of the et-basis vector actually shrinks to zero, which physically corresponds to time dilation going to infinity. This is the origin of the idea that an outside observer would never actually see anything cross the horizon of a black hole.
It’s also worth noting that all of this is perfectly valid for not just black holes, but for any spherically symmetric mass, like the Earth. In this case, the et-basis vectors also get shorter as one approaches the Earth.
The only difference here between the Earth and a black hole would be the parameter rs. In fact, a black hole is defined as any object that has its rs greater than its actual physical radius.
Therefore, for something like the Earth, the basis vectors will never shrink to a length of zero at any physically sensible value of r, because this would mean actually having to go inside the Earth to reach the Schwarzschild radius rs, in which case the Schwarzschild metric wouldn’t even be valid anymore.
But why does this happen? Why would the basis vectors getting shorter actually imply time itself passing slower near a black hole?
The answer to this really comes from the fact that time itself is only a coordinate in general relativity, not a universal concept.
Thus, any change in the coordinate system we use to describe spacetime will have an effect on the specific measured values of the coordinates.
In our case, the basis vectors changing length in the time direction means that the measured values of time at different points will also be affected.
Now, this may seem counter-intuitive, but if you actually wish to understand time dilation, you have to just accept the fact that time really is only a coordinate.
However, there is a concept of proper time, which can be thought of as the closest thing there is to a universal notion of time. I explain this later in this article (I also discuss this in my articles “Special Relativity For Dummies” and “Is Time a Vector?“).
Anyway, we can understand the geometry behind this time dilation effect through a simple example, which you’ll find down below.
If we’re talking about basis vectors changing in the time direction, surely this must have some kind of effect on actual vectors also, vectors after all being expressed through basis vectors?
The answer is actually somewhat more subtle, since a vector itself does not change even if the coordinate system (basis vectors) change but the vector components do.
To understand this, I need to first make clear that by vectors, I’m talking about four-vectors, which are basically vectors in spacetime (that have one time component and three spacial components).
Also, by a vector not changing, I’m essentially talking about its length (and direction, but that’s not too important for us) remaining constant. The length of a vector being invariant is one of the most fundamental geometric properties of vectors, so it will be true generally.
Anyway, let’s look at a concrete example of how time dilation actually occurs from this.
We’ll consider an object described by a spacetime displacement four-vector, which has a time component describing “displacement in the time direction” (which basically just means a time interval) and spacial components describing spacial displacements.
Moreover, we’ll take the object in question to be stationary in space, so the spacial displacements are all zero (the time component is not zero, however, since all objects “move in time”). You can physically think of this as an object that is essentially just “floating” above a black hole, for example.
The components of this four-vector are therefore:
dx^{\mu}=\left(cdt{,}\ 0{,}\ 0{,}\ 0\right)The c here is the speed of light, which is just a constant that is needed to give the right units to this expression.
The length of this four-vector is simply the total spacetime interval or line element, ds2 (actually, the square of the length). We can calculate this by the following formula:
ds^2=g_{\mu\nu}dx^{\mu}dx^{\nu}
This formula is basically the curved spacetime equivalent of the Pythagorean theorem. For more on this, I recommend reading my general relativity article. This metric tensor, gµν, is required here since the basis vectors are not constant.
Since the only non-zero component of the displacement four-vector is the time component, we get:
ds^2=g_{tt}dx^tdx^tFrom the example from earlier, we know that the gtt-component of the metric gives the square of the length of the time basis vector et. Inserting this and also the dxt-component, we get:
ds^2=g_{tt}dx^tdx^t=\left|\vec{e}_t\right|^2c^2dt^2Now, here comes the interesting part. Since the basis vectors get shorter as one moves closer to the black hole (this \left|\vec{e}_t\right|^2 -term gets smaller) but ds2 has to remain constant, this means that the dt2 MUST get bigger to account for the decrease in this basis vector length term.
But what does this mean physically? Essentially, this dt-term represents a displacement in time, in other words, a time interval. This term getting bigger the closer one moves to the black hole means time intervals are passing slower the closer one is to the black hole. This is the effect of time dilation!
This was just one example, of course, but the same concept still applies to other situations as well. Intuitively, you can think of the geometry of this time dilation effect the following way; since the basis vectors are shorter closer to the black hole, all vectors require “more of the time component” to describe that same vector.
Basically, the logic here is; shorter basis vector=”more” of the component to describe the same vector in that direction. This then results in actual physical effects in quantities that are described by components of four-vectors, such as time.
Quick tip: If learning the necessary math for general relativity is of interest to you, I think you would find my Mathematics of General Relativity: A Complete Course (link to the course page) extremely useful.
This course aims to give you all the mathematical tools you need to understand general relativity – and any of its applications like black holes and time dilation. Inside the course, you’ll learn topics like tensor calculus in an intuitive, beginner-friendly and highly practical way that can be directly applied to understand general relativity.
Does Time Stop In a Black Hole?
As one moves closer and closer to a black hole, the passing of time will also slow down more and more. So, does time therefore stop as one falls into a black hole?
Time does stop at the event horizon of a black hole, but only as seen by someone outside the black hole. This is because any physical signal will get infinitely redshifted at the event horizon, thus never reaching the outside observer. Someone falling into a black hole, however, would not see time stop.
Now, to understand what actually happens to time dilation at the black hole’s event horizon, we need to discuss an important distinction made by general relativity and that is the distinction between coordinate time and proper time.
Coordinate Time vs Proper Time
Coordinate time, in this context, is the time passing for the observer near the black hole as measured by another observer far away. In this sense, it is the amount of time an observer on Earth, for example, would measure to pass for the other observer near the black hole.
Proper time, on the other hand, is the time measured by the observer itself that is near the black hole. It’s worth noting that proper time is an invariant quantity, so in a sense, it is a more “objective” measure of the actual time that passes.
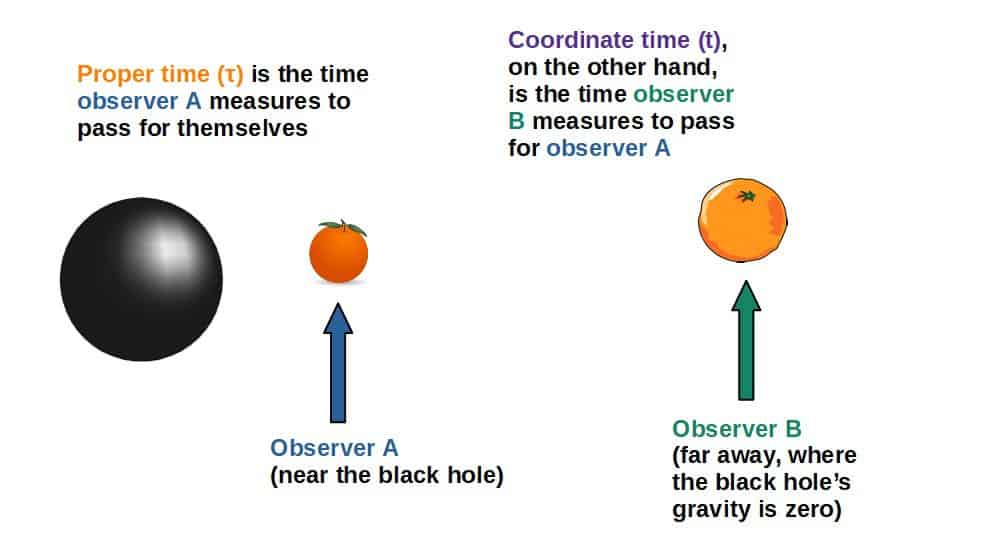
That being said, what really matters is the difference in the time measurements between the two observers, which results in the phenomenon of gravitational time dilation.
Mathematically, it’s possible to derive an equation for both the coordinate time (t) and proper time (τ) as a function of the distance (r) from the black hole’s center (note that these are only valid for stationary observers, because otherwise we’d have to account for other time dilation effects also):
t\left(r\right)=\frac{r_s}{c}\ln\left(\frac{\sqrt{r}-\sqrt{r_s}}{\sqrt{r}+\sqrt{r_s}}\right)+\frac{2}{3}\sqrt{\frac{r^3}{r_sc^2}}+\frac{2}{c}\sqrt{r_sr}Here, rs is the Schwarzschild radius, which describes the event horizon of the black hole (the radius beneath which nothing, not even light, can escape).
\tau\left(r\right)=\frac{2}{3}\sqrt{\frac{r^3}{r_sc^2}}From these, we can look at what happens near the event horizon of the black hole (in other words, the limit as r approaches rs).
Because of the logarithmic term in the first equation, the coordinate time blows to infinity, while nothing particularly special happens to the proper time.
So, the physical implication of this is that the far away observer would see the time passed for the observer near the event horizon slow down indefinitely, while the observer at the event horizon would not see anything special happening.
But why does such a thing happen? There is actually a fairly intuitive explanation for this, which all comes down to how we think of the concept of time; fundamentally, time can only be measured through changes.
Any measurement of a physical change is, however, limited by a “signal” having to travel between two points (between the observer and the point where the physical change occurs) and these signals are limited to travel at (or under) the speed of light.
This is the basic idea behind how the speed of light defines the way that the passing of time is measured (this is also the basis behind the idea of Einstein’s clock synchronization procedure).
This also helps us understand the phenomenon of gravitational time dilation.
Gravitational time dilation only happens between two observers at different points under different gravitational potentials and this is fundamentally due to how light (or any other signal) travels between these two points.
In case you’re wondering how light can be affected by gravity even though it has no mass, in general relativity, it can! This article explains exactly that issue in detail. In there, we also look at how light gets bent when passing by a star and we actually calculate the trajectories of light predicted by general relativity.
So, an observer far away (essentially not influenced by gravity at all) would observe the passing of time of another observer close to a black hole as being slower simply because light (or any other signal) is slowed down due to the gravitational potential difference between the observers.
Intuitively, you could think of this resulting from the gravity of the black hole “pulling” the outgoing light rays towards the center, thus “slowing them down”, but really this is due to the light being redshifted as it climbs out of the black hole’s gravitational well.
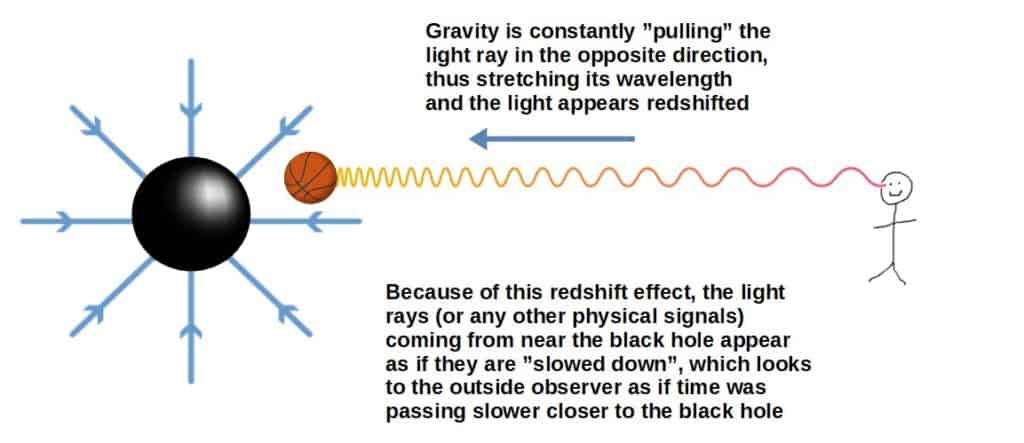
Now, while the far away observer would see any light rays or any other physical signals being slowed down due to gravity, thus resulting in the passing of time being seemingly slower, the observer near the black hole would not see such an effect.
This is because, locally, the speed of light is always c (a constant), so the time dilation effect is only due to the coordinate differences between the two observers.
The observer itself that is close to the black hole does not see his own time passing any slower, but the far away observer does see this other observer’s time passing slower.
But which one of them is right? Well, the answer is that both of them are correct.
See, the question isn’t about which one is more correct than the other because the whole premise behind this question does not make sense (relativistically, that is).
Neither one of them is more correct because this would require one observers frame being somehow “superior” to the other’s and the whole idea behind the theory of relativity is that all reference frames are equivalent.
So, it’s simply not possible to say how much time has “universally” passed, we can only say how much time passes in one particular frame and then compare those differences.
However, an objective fact is that there is a difference in the passing of time between the two observers. So, in fact, the two observers WILL see each other physically age at a different pace. This is discussed more later in the article.
How Much Does Time Actually Slow Down Near a Black Hole?
How much time actually slows down near a black hole will depend on a few things, such as the motion and position of the observer in question as well as the type of black hole and its properties.
We will keep considering the simplest types of black holes here, the Schwarzschild black hole, which are uncharged and non-rotating.
It’s worth noting, however, that the electric charge and rotation will play a role in time dilation for other black hole types, but these we will look at later in this article.
The simplest case we can do is consider an observer at a fixed position near the black hole (meaning that the observer’s spacial coordinates are constant, but the time coordinate is not; we’re essentially just ignoring all velocity-induced time dilation effects) and then compute the gravitational time dilation.
If this is the case, the gravitational time dilation is only affected by two things:
- The mass of the black hole
- The (radial) distance from the black hole
The formula for calculating the exact time dilation is as follows (note; this gives the time dilation factor, which is a dimensionless number):
\gamma=\frac{1}{\sqrt{1-\frac{r_s}{r}}}Here, rs is again the Schwarzschild radius (which depends on the black hole’s mass, since rs=2GM/c2), which gives the event horizon of the black hole. Note also that this formula is only valid for r>rs (i.e. outside of the black hole).
This time dilation factor essentially gives the ratio of proper time to the coordinate time (we talked about the differences between these earlier).
So, we can calculate the coordinate time that would pass for a given amount of proper time near the black hole by multiplying it with this time dilation factor:
\Delta t=\frac{\Delta\tau}{\sqrt{1-\frac{r_s}{r}}}As a reminder; proper time (τ) is the time that passes for the observer who is near the black hole, while coordinate time (t) is the time a far away observer would see pass for this observer near the black hole.
It’s interesting to look at some actual numerical values for the time dilation and how they depend on the distance from the black hole.
The most general way to do this is by specifying the distances from the black hole in terms of its Schwarzschild radius. This way we don’t have to specify a mass for the black hole or calculate the Schwarzschild radius explicitly.
Below I’ve collected a table of different values of the time dilation for different distances.
| Distance from the black hole (measured in units of rs) | Time passed on Earth for 24 hours near the black hole |
|---|---|
| 10 rs | 25.3 h |
| 6 rs | 26.3 h |
| 3 rs | 29.4 h |
| 1.5 rs | 41.6 h |
| 1.2 rs | 2.45 days |
| 1.05 rs | 4.58 days |
| 1.005 rs | 14.2 days |
| 1.0005 rs | 44.7 days |
| 1.00005 rs | 141 days |
The interesting thing about the above values is that the time dilation increases quite slowly, but as you get closer and closer to the black hole, the effects become much more significant and over time the effect sort of “compunds” on itself.
For example, if you were to spend 1 year near the black hole at the distance 1.00005 rs (which is probably unrealistic, since it is so close to the event horizon), in this time, 141 years would have passed on Earth!
Time Dilation Near Rotating and Charged Black Holes (Interactive Tool)
If we take into account other properties that a black hole may have (in general, a black hole can have a mass, charge and angular momentum), these will affect the time dilation experienced by an observer near the black hole, although the significance of these effects might vary.
Now, how would we calculate the time dilation in these more general cases? The general formula for the time dilation factor is:
\gamma=\frac{1}{\sqrt{-g_{\mu\nu}\frac{dx^{\mu}}{dt}\frac{dx^{\nu}}{dt}\frac{1}{c^2}}}If you’re not familiar with the mathematics of general relativity, this may look quite complicated. Implicitly, this formula contains a summation over both the µ and ν indices, which run from 0 to 3. These time derivatives of the coordinates describe the coordinate velocities.
This formula indeed gives the time dilation in any spacetime for any observer, moving or not. We can, however, simplify this a lot by only looking at observers that are stationary near the black hole (relative to the far away observer).
Doing this, the time dilation factor simplifies to:
\gamma=\frac{1}{\sqrt{-g_{00}}}
For stationary observers, the time dilation is only given by the g00-component of the metric.
Now, rotating and charged black holes in general relativity are described by the Reissner-Nordström metric (non-rotating black hole with charge), the Kerr metric (rotating uncharged black hole) and the most general one, the Kerr-Newman metric (rotating and charged black hole).
Sidenote: in case this article has been helpful so far and you’d like to download it as a PDF for yourself (or even print out), you can get a PDF version of this article here.
The g00-components of these metrics mentioned above are:
g_{00}^R=-\left(1-\frac{r_s}{r}+\frac{r_Q^2}{r^2}\right)\\g_{00}^K=-\left(1-\frac{r_sr}{r^2+a^2\cos^2\theta}\right)\\g_{00}^{KN}=-\left(1-\frac{r_sr-r_Q^2}{r^2+a^2\cos^2\theta}\right)The parameters a and rQ2 describe the angular momentum (“rate of spinning”) and charge of the black hole and they are defined as follows:
a=\frac{J}{Mc}{,}\ r_Q^2=\frac{Q^2G}{4\pi\varepsilon_0c^4}
Here, J is the black hole’s angular momentum, Q is its charge and M is its mass.
The time dilation factors obtained from these g00-metric components are then as follows:
\gamma_R=\frac{1}{\sqrt{1-\frac{r_s}{r}+\frac{r_Q^2}{r^2}}}\\\gamma_R=\frac{1}{\sqrt{1-\frac{r_s}{r}+\frac{r_Q^2}{r^2}}}\\\gamma_K=\frac{1}{\sqrt{1-\frac{r_sr}{r^2+a^2\cos^2\theta}}}Note that if we choose θ=π/2, this actually reduces to the Schwarzschild time dilation factor, meaning that in the θ=π/2-plane, the time dilation would appear as if the black hole was not rotating at all.
\gamma_{KN}=\frac{1}{\sqrt{1-\frac{r_sr-r_Q^2}{r^2+a^2\cos^2\theta}}}Here are a few noteworthy details about these time dilation factors:
- All of these reduce to the Schwarzschild time dilation factor if we take Q=0 and a=0.
- The time dilation factors for the rotating black holes depend on the θ-coordinate, which we’ll take as the angle relative to the z-axis (which is also the spin-axis of the black hole).
- Physically, this means that the time dilation as seen by a far away observer will be different depending on the relative angle between the far away observer and the observer near the black hole.
- This is due to a phenomenon called frame dragging, which can be thought of as the rotating black hole “dragging” the spacetime around it as it rotates (a nice analogue of this is like water “circling” around a drain in a pool).
- Also, due to this frame-dragging effect, all observers are naturally “dragged” to rotate with the black hole; thus, for an observer to remain stationary, it has to oppose the rotation of the black hole such that it remains still. This is only possible outside a certain distance called the stationary limit surface.
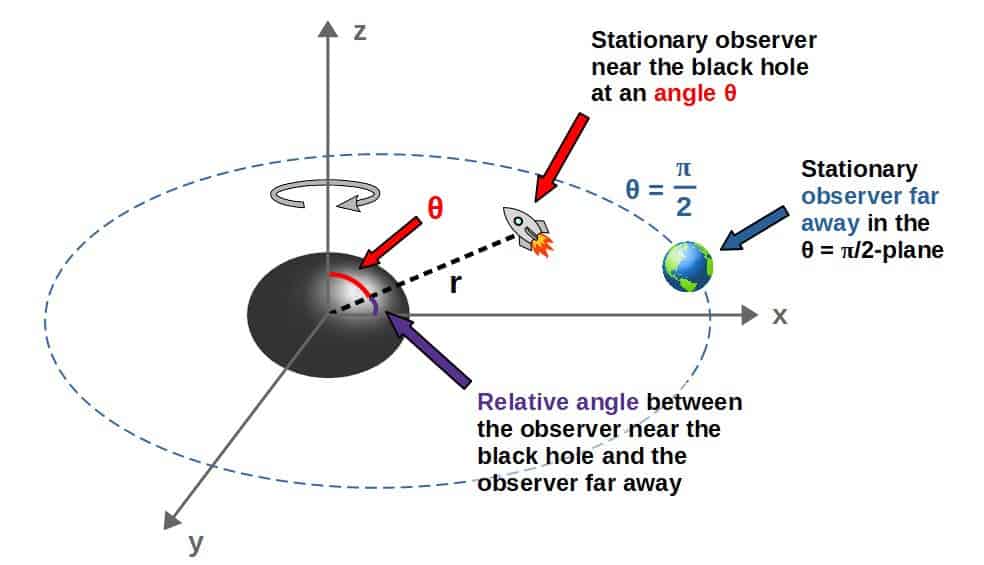
I explain the effect of frame dragging in more detail in this article. In there, I also go over how frame dragging actually results in some extremely interesting and complicated 3D orbital mechanics around a black hole.
To get an idea of how these time dilation factors for the different types of black holes actually differ from the simple Schwarzschild black hole, I’ve made a little interactive tool for you to play around with (which you’ll find down below).
This tool allows you to see the graphs of all the time dilation factors (plotted as functions of the r-coordinate) for different values of the black hole’s mass M and the angle θ. This allows you to visualize how these values actually affect the time dilation.
To turn on the animations in the graphs below, press either one of the sliding scales, then the top right corner with 3 bars, then the little gear icon (which reads “Object Properties”) and tick the “Animation On” -box.
Note; these functions plotted in the graph all describe extremal black holes (this makes it easier to compare them). This means that the black holes have the maximum possible allowed angular momentum and charge:
J_{\max}=\frac{GM^2}{c}{,}\ Q_{\max}=2M\sqrt{\pi G\varepsilon_0}The explicit time dilation factors are then (for simplicity, I’ve also set the constants c and G equal to 1):
\gamma_S=\frac{1}{\sqrt{1-\frac{2M}{r}}}{,}\ \gamma_R=\frac{1}{\sqrt{1-\frac{2M}{r}+\frac{M^2}{r^2}}}{,}\ \gamma_K=\frac{1}{\sqrt{1-\frac{2Mr}{r^2+M^2\cos^2\theta}}}{,}\ \gamma_{KN}=\frac{1}{\sqrt{1-\frac{2Mr-M^2}{r^2+M^2\cos^2\theta}}}Would You Really Age Slower Near a Black Hole?
Since black holes will affect the rate of time, it makes sense to think that they would also affect the way someone near the black hole ages. The question is, would you age slower or faster near a black hole?
In short, a person near a black hole will age slower compared to someone far away from the black hole. This is because the passing of time is slowed down due to the extremely strong gravitational field near the black hole and thus, any physical aging processes will also happen slower.
Now, let’s try to understand this more deeply.
When we talk about time dilation and time “slowing down”, we’re really talking about all physical processes slowing down to the same extent. In fact, we’re talking about all measurements of time being “slowed down”.
By time measurement, I don’t necessarily mean someone measuring seconds with a wristwatch, I’m rather talking about the fundamental nature of how time is even observed in the first place; through physical changes.
Think about it; if nothing were to ever change in any way, time would not even exist. There wouldn’t be any way of distinguishing the past from the present.
So, the passing of time itself can fundamentally only be observed by things changing and therefore, time slowing down really means that all physical changes happen slower.
The same applies to processes in your body as well. Essentially, this comes down to what aging really is in the first place; a series of physical processes that change your body over time.
These, on the other hand, are regulated by signals that your cells are sending across your body.
Now, it doesn’t really matter what these physical signals are; whether they are neuron impulses or hormone binding proteins travelling around your body, these are still physical processes of change, which too will be affected by gravitational time dilation as anything else would.
So yes, being near a black hole (or any other strong gravitational field) does affect aging. Now, the key point here is that a person near a black hole won’t themselves notice anything different in their OWN aging process, but another observer far away will.
It’s the difference in the passing of time that really matters when comparing who ages faster or slower.
In the language of general relativity, it’s the difference in the proper time (time as measured by the observer near the black hole) and the coordinate time (time as measured by some far away observer) that determines who ages at what rate COMPARED TO someone else (the word compared matters here, as the rate of aging is always relative to something).
