Is Time Actually A Vector or A Scalar? The Physics Explained

Often, we think of time as simply a number assigned to a specific event. However, time is also thought to always “flow” forwards, so could it therefore be considered as some sort of a vector?

From a modern physics viewpoint, time is not a vector nor a scalar, it is a coordinate. This is because time is relative depending on the observer, so it cannot be defined as a scalar or a vector. In Newtonian physics, however, time has a universal meaning and is usually thought of as a scalar.

In physics, there are a number of different interpretations of time. These can usually, however, be classified into two general views on the nature of time.

The two main perspectives are the classical or Newtonian perception of time, as well as the relativistic view of time, both of which differ from one another quite drastically.

At the end, I will also explain a very interesting theory in which time is actually a vector, but not in the usual sense; it is a bivector.

Why Is Time Usually Considered a Scalar?

The classical Newtonian picture of time is probably closest to the intuitive idea that we have about time as opposed to something like the theory of relativity.

In normal everyday life, we don’t think of time as having any weird, non-intuitive properties such as it being relative to different observers depending on motion or velocity.

Time is simply an invariant number (i.e. a scalar) that is assigned to, well, a specific point in time. This is exactly how time is described in Newtonian physics (the area of physics that is based on Newton’s laws).

Now, the key idea here is the word invariant, which we’ll explore next.

What Exactly Are Vectors and Scalars?

Let’s think about the definitions of scalars and vectors for a bit. The usual sort of a simplistic definition for a scalar is that a scalar only has a magnitude, not a direction, while a vector has both.

There is, however, a more fundamental definition, which comes up and in fact, plays a key role in more advanced theories such as relativity.

Essentially, a scalar in physics is something that is invariant under coordinate transformations. This simply means that if something is a scalar, it will have the same value no matter who is observing it. You can think of a scalar as basically just a number.

A coordinate transformation, you can think of as just a way to describe something in a different “reference frame” or from the perspective of a different observer. For example, a moving observer and a stationary observer have different coordinate systems to describe things, which are related by a coordinate transformation.

Vectors, however, require two pieces of information to describe them; a magnitude and a direction (angle). A vector also has a components in each direction (x-component etc.).

Now, a vector itself is always invariant under coordinate transformations, but its components can change. For example, a rotation is a type of coordinate transformation, which rotates the vector components (of course changing them), but the vector itself remains the same.

In more advanced physics, scalars and vectors are defined as mathematical objects that are invariant under coordinate transformations. This is much more fundamental than the naive definitions of “a scalar is something that only has a magnitude” and “a vector is something that has both a magnitude and a direction”.

This single property is enough to say that it certainly doesn’t make sense to describe time as a vector as time itself doesn’t have components (nor is it invariant under coordinate transformations in relativistic physics).

How Newtonian Physics Explains Time

In Newtonian physics, time is not thought of as being relative to different observers unlike in special relativity. It is therefore an invariant quantity and it also doesn’t have more than one distinguishable (orthogonal, if you will) component.

That is practically the definition of a scalar, so it’s fair to say that it makes more sense to describe time as a scalar.

Now, to be fair, what if we think of time as actually having a direction; it always moves forward, right?

Well, it still would not have more than one component, so does it really make sense to say it’s a vector? Sure, you might say that it’s a one-dimensional vector with only one component.

This, however, still does not change the fact that time is a scalar. If we think about time as a one-dimensional vector, that means that the magnitude of this vector is the same as its only component.

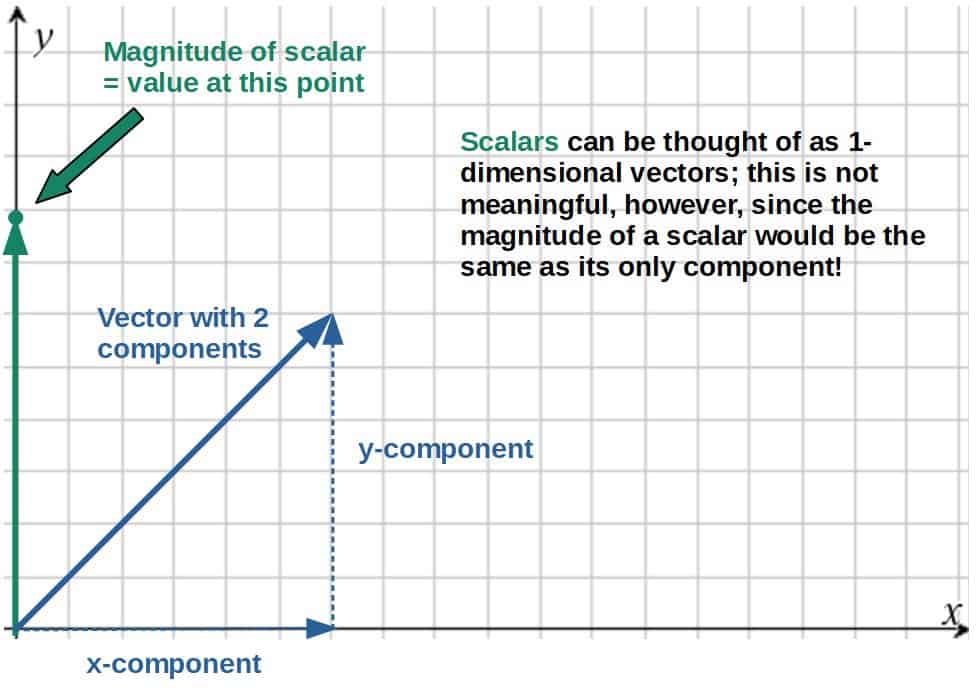
The magnitude of a vector, however, we know is a scalar (from the definition of dot products and other things). Therefore, the magnitude of a “time vector” being its only component, would mean that time has to be a scalar.

The bottom line here is that it makes more sense to think of time as a scalar rather than a vector (in Newtonian physics, that is).

The real problem comes from the fact that in relativity, time is not a universal concept, so it cannot be defined as a scalar.

Why Time Is Actually a Coordinate (In Special Relativity)

The concept of time viewed through the lens of special relativity is quite different from the classical Newtonian picture. You might have heard something like “time is relative” before, but how does this relate to the idea of time as a vector?

The basic principle of relativity is that the speed of light is a universal constant that everyone will measure to be the same independent of motion or (inertial) reference frame. The speed of light is actually the speed limit of the universe.

Anyway, this single fact that there is a constant speed limit in the universe leads to some pretty unintuitive consequences, especially in the context of time.

These include weird things such as time being dependent on motion and reference frames as well as space and time being able to mix together and transform into one another when switching from one reference frame to another.

Everything I’m going to talk about special relativity here is explained in much more detail in my introduction to special relativity.

Now, in relativity, space and time are both treated in a very similar manner and they can in fact, be combined into a single thing called spacetime.

This thing called spacetime, you can think of as being the “surface” in which everything in the universe takes place (really though, it’s just a useful tool to combine time and space to be able to describe things in what we call a covariant way).

But what does this have to do with time being or not being a vector? Well, the key idea is that all spacetime points are labeled by spacetime coordinates, which means one time coordinate and three spacial coordinates. Therefore, time is fundamentally just a coordinate.

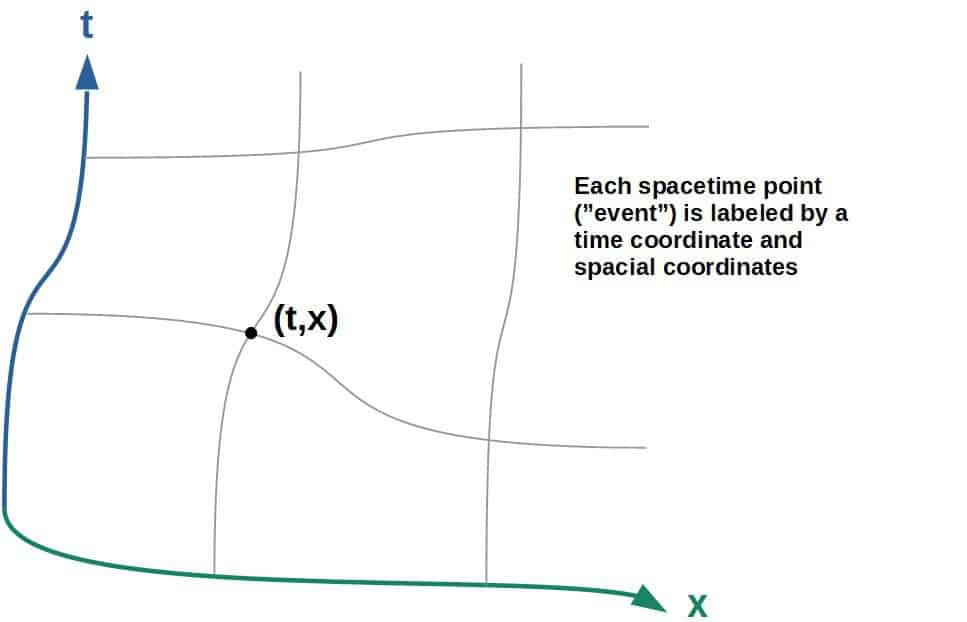
Here we have a “spacetime manifold” (it’s only two-dimensional in this case, so I could draw it as a simple coordinate system. Here, spacetime is also curved, so it’s actually described by general relativity). The key point is that we have both space and time directions (axes) and coordinates.

Now, it doesn’t make any sense to think of coordinates as vectors or scalars. They are simply just coordinates.

This is fundamentally due to the definitions of scalars and vectors, which are that they are invariant under coordinate transformations (a coordinate, of course, is not invariant under coordinate transformations; if we for example, were to change our time axis in some way, which is a form of coordinate transformations, the values for the time coordinates would be different).

As a sidenote; some people like to think of position in spacetime as a four-dimensional position vector (with a time and three space components), which would make time a vector component.

This, however, is not really correct, because “spacetime position” itself is not a well-defined concept (at least, not a well-defined vector) in general relativity, but spacetime displacements are. So, you could technically define a time interval as a vector component, but time itself is only a coordinate, nothing else.

This finally answers the important question here; is time a vector or a scalar? The answer is that time is neither a vector or a scalar, it is simply a coordinate label. That’s it.

If this seems hard to wrap your head around, I get it. However, this is how time is fundamentally viewed in modern physics; it’s simply a coordinate label and is only meaningful in the context of spacetime, but not really by itself.

Now, for everyday life, time can definitely be thought of as just a scalar, since the relativistic effects are really not observable in any way. But, just know that this is not the correct viewpoint that contemporary physics theories have about time.

My Mathematics of General Relativity -course will teach you all the math you need for a deep understanding of general relativity. You’ll find more information here.

Time As a Bivector

There is another formulation of special relativity, in which time is actually considered as a special kind of vector.

Essentially, this formulation is based on a field of mathematics called geometric algebra. Geometric algebra, on the other hand, is based on the mathematics of multivectors and geometric products.

I’m going to briefly go over these ideas and explain the logic behind viewing time as a bivector, but you can find out more about geometric algebra and its relation to physics in some of the papers I’ve linked to down below.

The basic idea behind multivectors and bivectors goes as follows:

  • A multivector can be thought of as a sort of generalization of regular vectors, and is a combination of scalars, vectors, bivectors, trivectors etc., meaning that it is a combination of higher-dimensional vectors.
  • Intuitively, think of an ordinary vector as a one-dimensional object. After all, it is just an arrow or a line and lines are one-dimensional objects. Scalars can then be thought of as 0-dimensional objects.
  • This idea can then be extended even further. A bivector is a 2-dimensional vector object, a trivector a 3-dimensional vector object and so forth.
  • Now, regular vectors can be built out of a basis (the x,y-basis in this case):
V=V_x\overline{\text{x}}+V_y\overline{\text{y}}

The Vx and Vy here represent magnitudes in each direction and the x and y with little lines above them are the basis vectors in the x and y directions.

  • A bivector can also be expressed in terms of basis bivectors (or unit areas, if you will). A basis bivector is simply the product of two basis vectors (they form an area with the unit vectors being the sides):
B=B_{xy}\overline{\text{x}}\overline{\text{y}}

Bxy is the magnitude of this bivector and the xy with a line above it is a basis bivector.

  • Just like vectors have a direction and a magnitude, so do bivectors. The magnitude of a vector is given by its length and for bivectors, their magnitude is given by their area in space.
  • When it comes to the direction of a bivector, it has two directional values (degrees of freedom), its orientation in space as well as a kind of rotational direction that depends on the vectors it is built out of.

Usually, the basis vectors are represented more generally with the letter e, for example:

\overline{\text{x}}=e_1\\\overline{\text{y}}=e_2

Now, the interesting thing about bivectors is that a unit bivector actually squares to -1 (just by how we choose to define it). For example, the square of a unit bivector e1e2 is:

\left(e_1e_2\right)^2=-1

But how is this useful for special relativity? The answer is that it actually provides a useful alternative for describing an interval in spacetime. The formula for a spacetime interval (S2) is:

S^2=-c^2t^2+x^2+y^2+z^2

This formula is basically the Pythagorean theorem in four dimension, except the time component has a minus sign.

The whole idea is that by using geometric algebra, the four-dimensional spacetime four-vector can be replaced by a three-dimensional spacetime multivector (call it X and the basis vectors is denoted by the e’s):

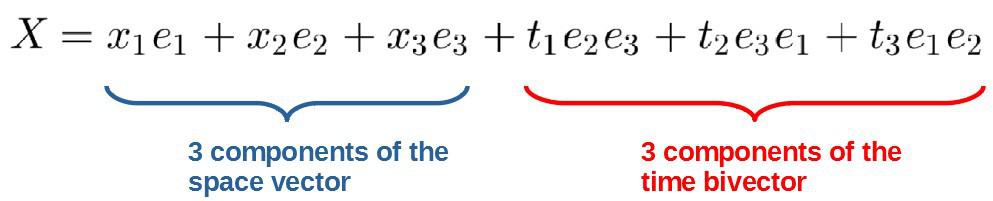
Here, the spacial position is given by a usual 3-dimensional vector, but time is given by a 3-dimensional bivector. The x1, x2 and x3 represent whatever space coordinates you wish to use (could be x,y and z).

When squared, this multivector will indeed produce the correct spacetime interval formula, which has a minus sign in front of the time component, which simply comes from the fact that a basis bivector squares to -1.

The mathematics of this is not too difficult and you can find more about it in this paper.

This, however, has some pretty interesting implications. First of all, this means that time does not have to be represented as its own dimension.

Based on this formulation, time is simply a bivector embedded in the 3-dimensional space rather than being a fourth dimension.

Secondly, this also implies that time can, in fact, be thought of as having three distinct components as seen above, which gives rise to some interesting ideas about the nature of time.

More accurately, these three components are actually associated with the rotational degrees of freedom (orientational directions of the basis bivectors) in 3-dimensional space.

Another consequence of this is that since bivectors naturally have to do with rotations, rather than flowing forward, time would flow circularly or rotationally. This idea also ties quite nicely into Kepler’s second law (source: Chappell JM, Iqbal A, Iannella N, Abbott D (2012) Revisiting Special Relativity: A Natural Algebraic Alternative to Minkowski Spacetime).

Ville Hirvonen

I'm the founder of Profound Physics, a website I created to help especially those trying to self-study physics as that is what I'm passionate about doing myself. I like to explain what I've learned in an understandable and laid-back way and I'll keep doing so as I learn more about the wonders of physics.

Similar Posts