Calculus of Variations For Dummies: An Intuitive Introduction
Most people have heard of basic calculus and know about its applications to, for example, geometry or physics. However, there is another area of mathematics called calculus of variations that is particularly important for physics.
Calculus of variations is the area of mathematics concerned with optimizing mathematical objects called functionals. Calculus of variations can be used, for example, to find the shortest path on a surface or in physics, to describe the motion of a relativistic particle under gravity.
In this article, we’ll look at exactly what these functionals are, what it means to optimize one and how calculus of variations is different from ordinary calculus you may already be familiar with.
We’ll also discuss some reasons why calculus of variations is important as well as how it’s applied in physics, geometry and other mathematical contexts.
As it turns out, calculus of variations is one of the most important areas of math used in physics, yet not many people know much about it. In this article, you’ll learn both why it’s useful as well as what it’s actually about.
Table of Contents
Why Do We Need Calculus of Variations?
First, we’ll go over why calculus of variations is important. This will also work as motivation for you to hopefully want to learn more about it.
Calculus of variations is an important topic in both physics and mathematical analysis. This is because it can be used to solve complicated optimization problems, which are important in all of modern science. In physics, calculus of variations is especially important for Lagrangian mechanics.
The main reason why calculus of variations is so important comes from the first thing mentioned above – solving optimization problems.
An optimization problem is simply a problem in which we want to maximize or minimize a particular quantity or mathematical object (possibly under some constraints as well).
An example would be to find the biggest margin of profit for a company, given a particular fixed budget – this is an optimization problem that could use the tools of variational calculus.
Optimization problems are hugely important in physics as well.
Actually, it turns out that solving for the trajectory of an object under a force is exactly an optimization problem. In particular, optimization of a quantity called the action – more on this later!
Below, you’ll find more examples of where calculus of variations is used for.
What Is Calculus of Variations Used For?
Calculus of variations is used, among other things, for the following:
- Finding paths of shortest distance (called geodesics).
- Finding surfaces of minimal surface area.
- Describing the motion of objects under gravity in general relativity.
- Deriving equations of motion for systems in Lagrangian mechanics.
- Modeling the dynamics of fields in field theories.
- Describing the motion of light rays in a material in the field of optics.
There still are many, many more applications of variational calculus in addition to the ones mentioned above.
However, hopefully these are enough to give you some motivation to move forward with learning more!
How Does Calculus of Variations Differ From Ordinary Calculus?
While calculus of variations is fundamentally based on the same mathematical tools as ordinary calculus (derivatives and integrals), they still differ from one another.
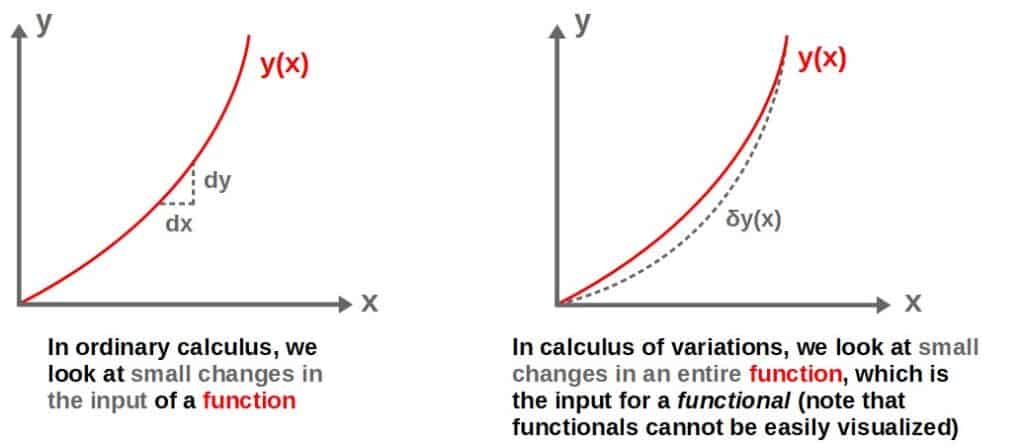
Calculus of variations differs from ordinary calculus by considering the optimization of objects called functionals as opposed to ordinary functions. Calculus of variations looks at changes in an entire function, while ordinary calculus only looks at changes in the values of a single function.
We could say that calculus of variations is a bit more general than ordinary calculus in the sense that calculus of variations deals with optimizing functionals, which themselves are more general mathematical objects than functions.
In ordinary calculus, we look at how the values of a function change with a small change in its input variable.
In variational calculus, on the other hand, we look at how the values of a functional change with a small change in its input, which itself is an entire function as opposed to a single variable.
So, we’re essentially looking at how a “function of a function” (called functional – more on these soon) changes with a small change in its input function.
With all of this being said, it’s now time to actually get to the details concerning calculus of variations!
Functionals Explained (With Examples)
In calculus of variations, the central mathematical objects of interest are called functionals. But, what exactly is a functional in the context of calculus of variations?
In calculus of variations, a functional is a mathematical object that takes in a function and returns a number. Mathematically, it is a mapping from the space of functions to the real or complex numbers. In a simple sense, a functional can be described as a “function of a function”.
So, a functional is a more general object than an ordinary function – a functional takes in an entire function as its input and returns just a number. This number describes the value of the functional for that particular input function.
In contrast, an ordinary function takes in just a number (the value of a variable x, for example) and returns another number that describes the value of the function for that input value.
Note; a functional is more generally defined as a mapping from a general mathematical space to the real or complex numbers. So, the input of a functional technically doesn't have to be just the space of functions.
For example, we could even think about the dot product with a given vector as a functional - this would take in a vector and return a number. In this case, this would be a functional that maps a vector from an inner product space to the real (or complex) numbers.
However, in the context of variational calculus, we will only consider functionals that take in a function and return a number (in most cases, a real number). That is, functionals that are mappings from the space of functions to the real numbers ("functions of functions").
So, we’re interested in functionals that take in some function – usually a single-variable function, such as a curve y(x) – and return a number. But how do we express such a thing mathematically?
Well, perhaps your first guess might be something of the form:
This would indeed be a “function of a function” – it takes in an entire function y(x) as its input.
However, this does NOT return a number, instead it returns another function of the variable x. For example, if you were to plug in y(x)=x2, you’d get F(x)=x4. So, this is not a valid functional.
Generally, a valid functional that takes in a full function and returns just a single number can be obtained by writing the functional as a definite integral.
For example, something of the following form would be a valid functional:
This now takes in a function y(x) and returns just a number (crucially, the same number for all values of the variable x). We can see this by plugging in, for example, y(x)=x2 which gives the following value of F:
Generally, we write functionals in the form of a definite integral in the context of variational calculus.
For a general functional, its integrand (the expression inside the integral) does not have to involve just y(x), it can also involve x itself, the derivative of y(x), dy(x)/dx, or any number of higher derivatives of y(x).
However, we’re usually interested in functionals with their integrands only involving x, y(x) or dy(x)/dx and not other, higher derivatives. These are generally the most useful types of functionals in most areas of math and physics.
So, a general functional we’re going to look at in this article would be written as:
The reason such functionals are interesting to us is because of reasons related to an incredibly important area of physics called Lagrangian mechanics – we will discuss this later.
Functionals of the above form are also encountered in geometric applications quite often.
For example, the length of a curve y(x) in the xy-plane between two points (x=a and x=b) is described by the arc length functional, which can be explicitly written as:
Functions vs Functionals
For a quick recap, here is a table comparing the main differences between ordinary functions and functionals (in calculus of variations):
| Function | Functional |
|---|---|
| Takes in a number as input | Takes in a function as input |
| Returns a number | Returns a number |
| No general form | Generally expressed as a definite integral |
| Changes described by ordinary derivatives | Changes described by functional derivatives |
Above, you’ll see something called a functional derivative mentioned. Let’s discuss this next.
Functional Derivatives: What Are They?
In ordinary calculus, the most important mathematical concept is the derivative of a single-variable function.
Similarly, in calculus of variations, the most important mathematical concept (after functionals) is that of a functional derivative.
A functional derivative is analogous to an ordinary derivative, however, a functional derivative considers the change in a functional with respect to a function (in contrast to the change in a function with respect to a variable in ordinary calculus).
We denote the functional derivative of a functional F(y) with respect to a function y(x) with the symbol δ as follows (compared to df(x)/dx for an ordinary derivative):
Essentially, this has the same meaning as the ordinary derivative of a function – it describes the rate of change of the functional F(y) when we change its input function y(x) by a little bit.
This “change in the input function y(x)” is denoted by this δy here (it’s very common to denote small changes by the symbol δ).
The Variation of a Functional
In multivariable calculus, there is also the concept of the total differential of a function. For example, the differential of a multivariable function f(x,y) is given by:
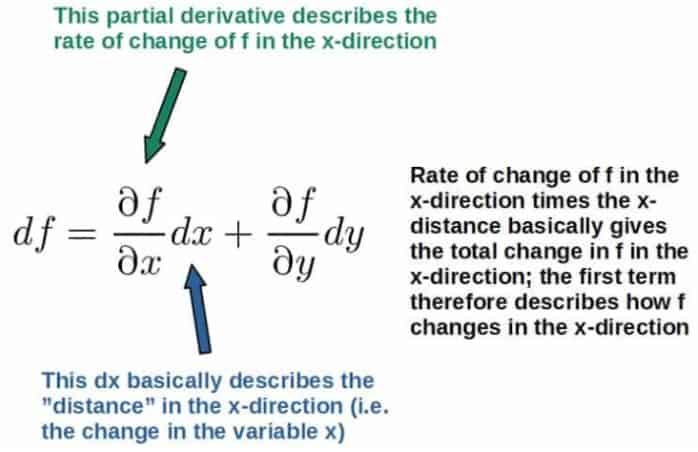
Similarly, there is an important concept in calculus of variations called the variation of a functional. This is basically the analogue of the total differential of an ordinary multivariable function, so in a sense, it described the “total change in a functional”.
We usually denote the variation of a functional F(y) as δF(y).
The variation of a functional is important when considering, for example, the Euler-Lagrange equation (which we will discuss soon).
Now, how do we represent the variation of a functional?
Well, your first guess might be that it has a similar form to the differential of an ordinary multivariable function (a sum over the partial derivatives of the functional multiplied by the change δy):
There is just a couple things wrong with this definition. First, the partial derivative here should be replaced by the functional derivative δF/δy – we’re talking about functionals and not ordinary functions here, after all.
Moreover, this sum here should represent a sum over all the “input variables” of the functional F(y). However, there is a continuous range of values for these “input variables” y(x), one value y(x) for each x, since these “input variables” y(x) here are themselves continuous functions.
Now, how do we represent a sum over an infinite, continuous amount of “variables”?
Well, by an integral! Namely, an integral over all the values of the independent variable x between the points x=a and x=b, where the functional is defined between.
The differential or variation of a functional F(y) is therefore written as:
In practice, when finding functional derivatives, we often define δF on the left-hand side in terms of a limit (just like in ordinary calculus), calculate the limit and then identify δF/δy.
For example, it’s possible to derive a general result that the functional derivative of any functional written as a definite integral is given by:
This is the functional derivative of a general functional that can be written as:
The Euler-Lagrange Equation
One of the most important results in calculus of variations is the Euler-Lagrange equation. It is often taken as the starting point to solve any calculus of variations problem. But what is the Euler-Lagrange equation?
In short, the Euler-Lagrange equation is a second-order differential equation that any functional has to satisfy in order to have a stationary value. The solutions of the Euler-Lagrange equation are functions that make a given functional stationary.
The Euler-Lagrange equation specifically applies to functionals written in the form of a definite integral that we’ve been discussing throughout this article:
The Euler-Lagrange equation applied to such a functional is then:
This is the Euler-Lagrange equation applied to a functional of the function y(x). Notice that the Euler-Lagrange equation specifically involves the integrand function f(x,y,y’) of the functional F(y).
Now, with the concepts of functionals and functional derivatives discussed, we can now understand the Euler-Lagrange equation and what it tells us.
With the Euler-Lagrange equation, we also finally get to the main application of variational calculus – optimizing functionals.
What Does The Euler-Lagrange Equation Tell Us?
As mentioned earlier, the Euler-Lagrange equation is the condition that any functional has to satisfy in order for the functional to have a stationary point.
Specifically, the solutions to the Euler-Lagrange equation – it’s a differential equation, after all – are the functions y(x) that make a given functional F(y) stationary.
Now, you may ask; what even is a stationary point of a functional? To answer that, let’s go back to ordinary calculus again.
In ordinary calculus, we often want to find the minima or maxima of single-variable functions.
For example, we could have a function that describes the current in an electric circuit as a function of time and finding the maxima of this function would equate to knowing when the current is the biggest.
Together, the minimum, maximum or saddle points of a function are called stationary points.
We find the stationary points of a single-variable function f(x) by setting its first derivative equal to zero (df(x)/dx=0) and solving for the values of x that satisfy this.
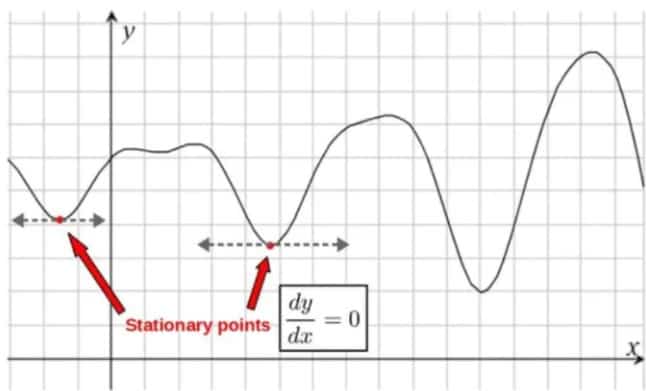
Solving the equation df(x)/dx=0 for a given function gives us the value of the variable x at which the function is at a stationary point.
Now, the story is not too different in calculus of variations. In calculus of variations, we often want to find stationary “points” of functionals.
The only difference, however, is that the stationary “points” of a functional are not really points, but entire functions – functions that make stationary (minimize or maximize) a given functional.
Just like the stationary points of ordinary single-variable functions are found from the condition that df(x)/dx=0, stationary “points” of functionals (i.e. functions y(x)) are found by setting the functional derivative equation to zero (or equivalently, the variation δF), δF/δFy=0.
Earlier, we found that in general, the functional derivative of any functional written as a definite integral is given by the following expression:
The stationary “points” of the functional would then be given by setting this equal to zero, in other words:
This is exactly the Euler-Lagrange equation! From this, we can see that the Euler-Lagrange equation is nothing but a direct result of setting the functional derivative (or variation) of a functional equal to zero.
Hopefully, this also makes it clear why the Euler-Lagrange equation indeed gives the condition for a functional to be stationary.
There is also quite an interesting interpretation of the Euler-Lagrange equation that comes from physics. More specifically, from a formulation of physics called Lagrangian mechanics.
In Lagrangian mechanics, the Euler-Lagrange equation can be thought of as a more general version of the famous Newton’s second law, F=ma.
We’ll discuss this more later, but if you want the full story, I would recommend reading my introduction to Lagrangian mechanics, which you’ll find here.
How To Use The Euler-Lagrange Equation (4 Simple Steps)
At this point, we pretty much have all the tools we need to apply calculus of variations and the Euler-Lagrange equation in practice.
The basic framework for solving a calculus of variations problem using the Euler-Lagrange equation can be summarized in the following four steps:
- Write down a functional F(y) describing the problem in the form of a definite integral over some function f(x,y,y’).
- Identify the integrand function f(x,y,y’). You’ll need this for the Euler-Lagrange equation.
- Write down the Euler-Lagrange equation for the function f identified in the last step.
- Solve the resulting differential equation for y(x). This is the function that makes the original functional F(y) stationary.
The goal of these steps and of any calculus of variations problem is to find the function y(x) – the function making a given functional stationary.
Why exactly we would want to find the stationary functions y(x) of a functional will, of course, depend on the problem.
You’ll find an example of this below. This is perhaps the simplest calculus of variations problem, in which the goal is to find a curve y(x) that describes the shortest distance between two points on a plane.
In this example, we want to find the path of shortest distance between two points on a plane using the calculus of variations framework we’ve just developed.
We can describe this problem using the standard Cartesian x,y -coordinate grid.
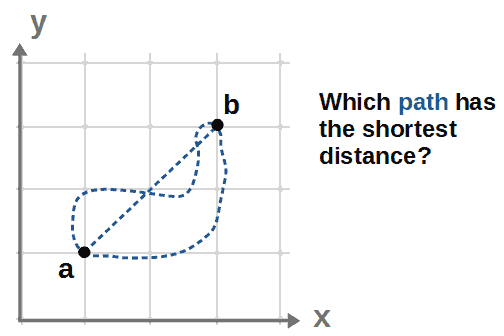
First, we need to find a functional that describes the length of this path or the distance from a to b. We can then use the Euler-Lagrange equation to find some curve y(x) in the x,y -plane that minimizes this functional, in other words, gives us curve of shortest distance between the two points.
The key to this is that no matter which curve we have between the two points a and b, we can always break it down into small small “pieces of distance” along the curve:
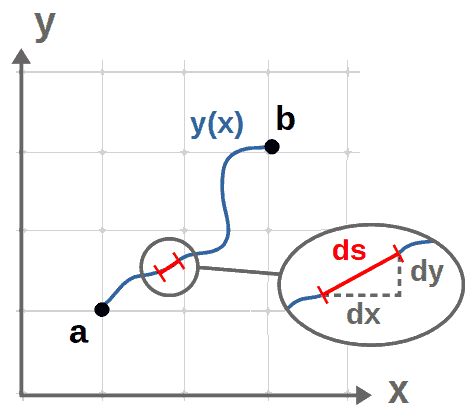
If these ds-pieces are small enough (infinitesimal, to be precise), they look exactly like straight lines and we can apply the Pythagorean theorem:
This describes a small distance along any curve y(x) on the x,y -plane. We can get the total distance s between the points a and b by integrating all these ds-pieces:
This might look like a weird thing to write down since we don’t have anything we’d be integrating with respect to here. We can fix this by factoring out dx2 from inside the square root:
Here, dy/dx is just the derivative of y(x), which we’ll denote as y’.
We now have a functional that gives us the distance along any curve y(x) between the two points a and b:
This functional is actually quite important in many geometric applications – it’s often called the arc length formula as it describes the arc length along a curve y(x) between two points.
To find the curve y(x) that minimizes the distance functional s(y), we use the Euler-Lagrange equation on the integrand function:
Let’s first calculate the partial derivatives of this function we need for the Euler-Lagrange equation. In particular:
Plugging these into the Euler-Lagrange equation, we find:
Here we have the total derivative of something being equal to zero – this means that the thing inside the parentheses is a constant, which we’ll call C. This allows us to get rid of the d/dx-derivative, giving us the following first-order differential equation:
This is now a differential equation we can solve to find the curve y(x) we’re interested in. To do this, let’s square both sides and solve for y’:
This thing on the right-hand side is just another arbitrary constant, which we can call A. We can then integrate both sides (reminder; y’=dy/dx) to get:
This, of course, is the equation for a straight line, which is what you might have expected – the shortest distance between two points on a plane is a straight line. This was the calculus of variations method to derive this.
In more complicated cases, we may want to find the shortest distance between two points on a curved surface (a sphere, for example), in which case the result won’t be as simple as a straight line.
In general, this is the problem of finding geodesics – paths of shortest distance between two points – which is an incredibly important application of variational calculus. We’ll talk about geodesics a bit later in this article.
Beltrami Identity: A Special Case of The Euler-Lagrange Equation
Before we look at various applications of variational calculus, it’s worth going over a really useful special case of the Euler-Lagrange equation – the Beltrami identity.
The Beltrami identity applies whenever we have a functional F(y) with the integrand function not depending explicitly on the variable x – in other words, of the form f(y,y’).
Written more explicitly, the Beltrami identity would therefore be applicable to functionals of the form:
Of course, y and y’ still do depend on x, so the integrand function f still depends on x, but only implicitly through the x-dependence of y and y’.
Mathematically, the statement that f does not explicitly depend on x means that ∂f/∂x = 0.
Now, whenever this is true, we can prove that the Euler-Lagrange equation reduces to the following form:
This is called the Beltrami identity. It’s a special case of the Euler-Lagrange equation and it applies whenever we have ∂f/∂x = 0.
Now, why is the Beltrami identity useful? Well, in many cases where it’s applicable, it’s much simpler to use than the full Euler-Lagrange equation itself – the Beltrami identity only requires us to take a single derivative, ∂f/∂y’, and nothing else.
So, the Beltrami identity is a useful special case of the Euler-Lagrange equation, which can be used in certain situations to simplify things.
The Beltrami identity also plays a key role in Hamiltonian mechanics – an alternative formulation of classical mechanics – in particular, for giving a nice interpretation to the Hamiltonian function.
Applications of Calculus of Variations
We’ve now covered the main concepts used in calculus of variations.
There is a lot of interesting theory behind this topic that we did not cover, but for now, we’re going to shift our focus to the practical applications of variational calculus instead.
Below, you’ll find some discussion as well as examples of how calculus of variations is used in various areas throughout mathematics and physics.
Calculus of Variations In Geometry
One of the major areas of application of calculus of variations is in geometry.
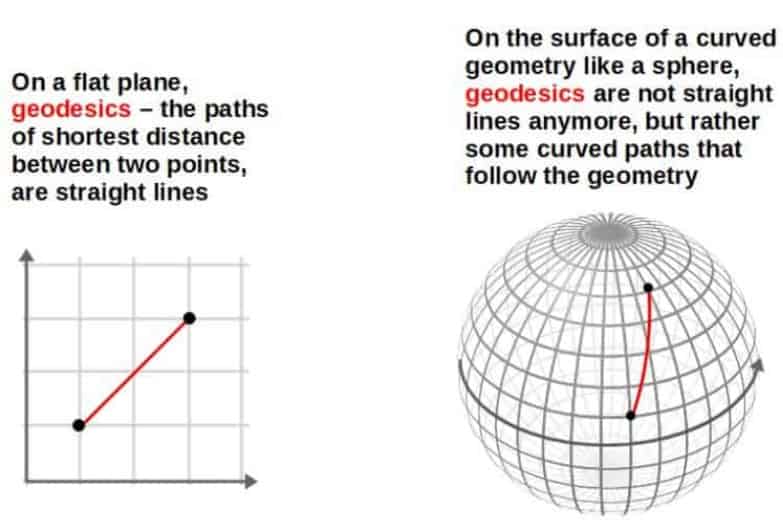
One of the most important of these geometric applications is for finding geodesics on various surfaces. A geodesic is essentially the shortest path between two points.
When we typically think of two points and some path joining them, a straight line naturally comes to mind – the shortest distance between two points is a straight line.
However, this is only true when we talk about a flat geometry, such as a plane. If we’re on the surface of some curved geometry, geodesics are more complicated as they are constrained to the geometry of that particular surface.
Now, how is all of this described in calculus of variations?
Well, we describe distances along surfaces by integrating along some curve on the surface. These integrals describing distances generally have the form of a functional.
Then, if we want to minimize these distance functionals (find the shortest possible distances – geodesics), we use the tools of variational calculus like the Euler-Lagrange equations. This naturally lends the problem of finding geodesics to calculus of variations.
Finding geodesics is incredibly important in areas of mathematics like differential geometry. In differential geometry, we’re often looking at spaces or geometries that can be described by a so-called metric tensor (usually denoted as gij).
The metric tensor essentially allows us to describe all distances in a given geometric space. The distance is given by a functional that has the following form:
Without getting into the details too much, this is essentially a generalization of the standard arc length formula that describes the distance in any metric space – most importantly, however, this has the form of a functional.
Now, using the Euler-Lagrange equation, it’s possible to derive a general equation that describes the curves of minimum distance between any two points on any surface with a metric.
This is called the geodesic equation:
These Γimn-objects here are called Christoffel symbols. I discuss their geometric meaning (and physical meaning in general relativity) more in my Complete Guide To Christoffel Symbols.
While the above equation might look somewhat complicated, it’s incredibly useful – the geodesic equation is a general “formula” for calculating geodesics in any space with a metric.
The geodesic equation has applications in general relativity, among other thing. In general relativity, the paths that objects take through spacetime under the influence of gravity are always geodesics.
In other words, anything under the influence of gravity moves along a geodesic and the geodesic equation is used to calculate these paths by specifying a given spacetime metric.
This can be used to predict the relativistic deflection of light around a star, orbits around a black hole as well as many other interesting things.
However, doing all of this is only possible because we have the tools of variational calculus at our disposal. If it wasn’t for calculus of variations, we wouldn’t have such a reliable and practical way to find geodesics.
So, at least if you’re planning to learn general relativity or differential geometry, I would highly recommend getting good at calculus of variations!
There are also various other geometric applications of calculus of variations. Here’s a list of some of them:
- Finding geometric shapes that minimize a particular quantity – this could be to find the shape of a hanging chain which minimizes its potential energy, the shape of a surface with minimal surface tension or the curve that minimizes the fall time of an object under gravity.
- Maximizing a particular quantity under a geometric constraint – often referred to as isoperimetric problems, an example of this would be to find the shape of maximal surface area with a fixed perimeter length.
- Finding trajectories of light rays in geometric optics – this is more of a physics application, however, it is also a geometric problem as it turns out that light rays will take on differently shaped trajectories in different materials.
A noteworthy thing to mention about the second point is that these types of problems with constraints often require the use of something called Lagrange multipliers, which we haven’t discussed in this article.
I discuss Lagrange multipliers more in my article on constraints in Lagrangian mechanics. The article is more geared towards physics, but I also explain the geometric meaning of the Lagrange multipliers there.
Calculus of Variations In Classical Mechanics
Perhaps the most important application of calculus of variations in physics comes from classical mechanics – or more precisely, Lagrangian mechanics.
In fact, Lagrangian mechanics forms the basis of how we describe nature in many of our current physical theories – examples being general relativity and quantum field theory, two of the most accurate theories in modern physics.
We’ll talk more about these soon in the context of field theory, but first – how is calculus of variations used in classical mechanics or Lagrangian mechanics?
In short, it turns out that we can describe any physical system by a quantity called action. The action is related to the kinetic and potential energies in the system, but more importantly, it has the form of a functional.
Then, the actual physics of the system (such as how the system evolves in time) is obtained by minimizing the action. This goes by the name of the principle of least action.
Of course, minimizing a functional is naturally a calculus of variations problem – therefore, describing the physics and time evolution of any classical system can be done by using calculus of variations.
It also turns that doing it this way – by using calculus of variations and the principle of least action – has many advantages compared to, for example, the standard way of applying Newton’s laws.
All in all, this formulation of classical mechanics where we use calculus of variations and the action principle is called Lagrangian mechanics.
I actually have a full beginner-friendly introduction to Lagrangian mechanics (found here), in case you’re interested in learning more about it.
As one last point, in Lagrangian mechanics, we use the Euler-Lagrange equation to describe the physics of a system.
However, there is a formulation of classical mechanics that also uses calculus of variations, but instead of the Euler-Lagrange equation, it takes advantage of the Beltrami identity.
This formulation goes by the name of Hamiltonian mechanics, which I also have a full introduction to (found here).
Calculus of Variations In Field Theory
Field theory is the area of physics concerned with describing physical objects called fields – for example, the electromagnetic field or even the Higgs field if we’re talking about a quantum field.
Field theory actually consists of quite a wide range of different things – there isn’t just one field theory, but many field theories, depending on what we physically want to model. However, there are certain aspects that all field theories have in common.
Field theories underlie most of the currently accepted modern theories of physics, such as general relativity, electromagnetism or quantum field theory.
Now, the area of mathematics behind field theory is largely – as you may have guessed – calculus of variations.
Calculus of variations is actually used quite similarly in field theory as it is used in Lagrangian mechanics – but in a more complicated manner, in some sense.
In field theory, we typically describe the dynamics of a field by constructing an action for the field. This action is defined through something called a Lagrangian density over all of spacetime.
The Lagrangian density itself is a function of spacetime coordinates and the field we want to describe (that is also a function of spacetime coordinates).
Now, we won’t get into the specifics here, but essentially, the action for a field has the form of a functional (similarly to how the action for a single particle is a functional in Lagrangian mechanics, as explained previously).
In field theory, we also have the principle of least action.
This states that the dynamics of a field are obtained by minimizing the action – which being a functional, of course, requires the tools of variational calculus.
When we minimize the action for the field, we’ll end up with a “more general” form of the Euler-Lagrange equation, which gives us the field equations for a given field theory.
For example, in electromagnetic field theory, these would be Maxwell’s equations and in general relativity, these would be the Einstein field equations.
By the way, if you want to see exactly how the Einstein field equations are obtained by using calculus of variations and the principles of field theory, I recommend checking out this article.
Now, all of this was to just highlight the fact that calculus of variations is applied in MANY areas of advanced physics – it is used extensively in classical mechanics, electromagnetism, special relativity, general relativity, quantum field theory and many more areas.
The point is that calculus of variations is one of the most important areas of math to understand if you really want to understand advanced physics on a deeper level.
Where To Learn More About Calculus of Variations?
For those of you who want to learn more about calculus of variations and about how it is applied in physics, I have to mention my own Advanced Math For Physics: A Complete Self-Study Course (link to the course page).
The aim of the course is to teach you the most important mathematical tools you’ll encounter everywhere in advanced physics – one of them being calculus of variations.
If you want to specifically learn about how calculus of variations is applied in physics, this course is going to be perfect for you.
The course starts from the very basics – like ordinary single-variable calculus – and eventually builds up to teach you about functionals, the Euler-Lagrange equations, the Beltrami identity and even constrained optimization and Lagrange multipliers.
In each lesson, I show you lots of examples of how each concept is applied in physics – so this isn’t just an abstract math course.
With the course, you’ll also get a calculus of variations workbook with practice problems you can do yourself as well as a solution manual with my step-by-step solutions to each problem.
If you want to check out the course, just go to this page.
As a final mention for those of you who wish to specifically learn about Lagrangian mechanics and field theory, I’d recommend checking out my book Lagrangian Mechanics For The Non-Physicist (link to the book page).
This book will teach you all about Lagrangian mechanics starting from Newton’s laws and then building up to topics like Noether’s theorem and field theory.