How Gravity Affects Photons & Light: A Complete Physics Guide
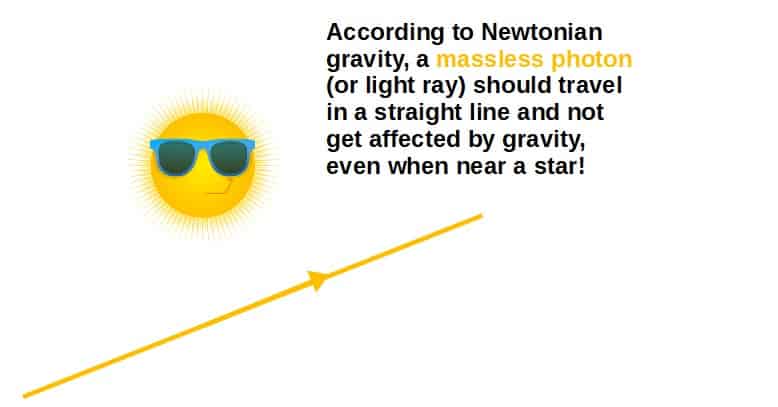
We know that photons have no mass and we like to think that gravity only affects things that have a mass. However, photons still get deflected by the Sun and can even orbit around a black hole. How exactly are photons being affected by gravity then?
Photons have no mass, but they are nonetheless affected by gravity due to the bending of spacetime itself. In the presence of gravity, photons travel along geodesics. Geodesics depend on the geometry of spacetime and photons moving along a curved geodesic will appear to be affected by gravity.
In this article, we’ll look at how Newton didn’t quite get it right with gravity, what gravity really is, how general relativity describes gravity and how this all relates to tell us how massless photons are affected by gravity.
If you’re wondering why exactly photons do not have mass in the first place, I have a full article covering that here. I also cover why photons still have momentum, even though they have zero mass in this article.
Table of Contents
Does Newtonian Gravity Affect Photons?
The first and longest standing theory of gravity was Newton’s theory. This comes nicely within the framework of Newton’s laws,
- Law 1: A body stays at rest, or travels in a straight line at constant speed, unless acted on by a force.
- Law 2: Force equals mass times acceleration F = ma.
- Law 3: Every action has an equal and opposite reaction.
Newton’s theory of gravity fits on the left-hand side of the equation in his second law. This is the formula telling us the force of gravity due to a body of mass M on a second body of mass m that are separated by some distance r:
F=-G\frac{Mm}{r^2}Here G is the gravitational constant – a number fundamental to the universe that tells us how strong gravity is.
The minus sign is a bit of mathematical convention that tells us that the force is attractive!
Let’s put this force to action with a body such as a star with mass M and a photon with mass m. Starting with what we know, photons have mass m=0, so let’s plug that in here:
F=-G\frac{M\cdot0}{r^2}=0Here we’ve arrived at Newton’s interpretation of how light is affected by gravity – it isn’t! No massive object will affect a photon according to Newtonian gravity!
We can apply all of Newton’s laws here – his third law tells us that the photon also doesn’t exert a force on the star and his first law tells us that since there is no force of gravity acting on the photon, the photon travels in a straight line!
These laws seemed infallible for a long time – they described everything we saw on Earth well for a long time. An issue came up with the orbit of Mercury.
The technical term for this is orbital precession but we’ll get on to what that exactly means in a moment. First, we just need to know one fact: orbits in Newtonian gravity are ellipses – they look like squashed circles.
These ellipses slowly rotate over time as the planet orbits – this is orbital precession and is predicted in Newtonian gravity. However, the amount Mercury should precess according to Newtonian gravity versus how much astronomers saw did not agree.
This was one of the first hints that Newtonian gravity were not complete!
However, Newton’s laws stood the test of time until Einstein came along with a new perspective on gravity known as the theory of general relativity.
Why Gravity Affects Photons In General Relativity
Next, we’ll look at how Einstein’s theory of general relativity, a more accurate description of gravity, explains why photons indeed are affected by gravity like all other forms of matter.
Specifically, we’ll discover that:
- In general relativity, photons always travel along geodesics.
- Geodesics can be thought of as the shortest paths between two points.
- In general relativity, the shortest path between two points might not always be a straight line.
- Sometimes the shortest distance a photon can take between two points may actually be along a curved path, in which case it would appear to us that gravity has an effect on the photon’s path.
Now, what determines the shortest distance between two points? In general relativity, it is the curvature of spacetime. The geodesics of photons appear as different paths depending on how spacetime is curved.
Einstein formulated the concept of “spacetime”, meaning that we look at space and time equally as one greater concept, rather than as time being some universal ticking clock.
Einstein’s theory of relativity does away with the idea that gravity is a force and replaces it with the idea that gravity is the bending of spacetime due to matter! This can be summarized as:
“Spacetime tells matter how to move, matter tells spacetime how to bend.”
Einstein’s theory has to be a geometric theory in order to talk about the shape of spacetime so it is all described in a new mathematical language.
To truly understand how and why gravity affects photons, we need to dive into the mathematics of general relativity a little bit and see how exactly Einstein predicted the bending of light and the trajectories of photons.
If general relativity is something you’d be interested to learn more about, I have a full introductory article called General Relativity For Dummies: An Intuitive Introduction. The article gives you a full overview of what general relativity is about and teaches you the most important concepts in an intuitive sense.
I also have a full guide on learning general relativity on your own, if that’s something you’re interested in doing.
A Brief Introduction To The Mathematics of General Relativity
In Newtonian physics, we can talk about how things change with time, we can talk about, say, the position of a car at time t = 0, t = 1, t = 10 etc. We would write this position x(t) as x(0), x(1), x(10). Time is special and can “parameterize” the path that the car takes.
In general relativity, time is no longer special and is put on an equal footing with spatial coordinates. We describe everything using the concept of spacetime, which means that paths need to also be parameterized in a different way than by using time.
Paths in spacetime are called worldlines and we write them as xµ(λ). The upper µ labels four coordinates (µ = 0,1,2,3) and can be represented as a vector (called a four-vector):
x^{\mu}\left(\lambda\right)=\begin{pmatrix}x^0\left(\lambda\right)\\x^1\left(\lambda\right)\\x^2\left(\lambda\right)\\x^3\left(\lambda\right)\end{pmatrix}We’ve now seen the notation xµ(λ) or x(t) but what does this mean? We treat the coordinates like functions. In these two cases they are either functions of λ or of t, time!
This means that if you plug in some number for time or the “parameter variable”, the function will give you what xµ or x is at that time or parameter value.
Using a general path parameter λ in general relativity is just a mathematical tool to allow us to parameterize paths of particles in a similar way as in Newtonian physics, where time does this for us.
Now, most of us have heard of Pythagoras’ theorem; this relates two sides of a right angled triangle to its hypotenuse, most famously as a2+b2=c2.
What this is secretly telling us is that the diagonal line between any two points is the shortest distance between those two points (mathematically, this follows from the fact that for two positive numbers a and b, \sqrt{a^2+b^2}<a+b. This goes with our intuition that the shortest distance between two points is the line connecting them.
The maths of general relativity uses ideas exactly like this. If we want to talk about the surface of a shape, we think about how the shape changes on very small length scales – this is the same intuition as what derivatives are!
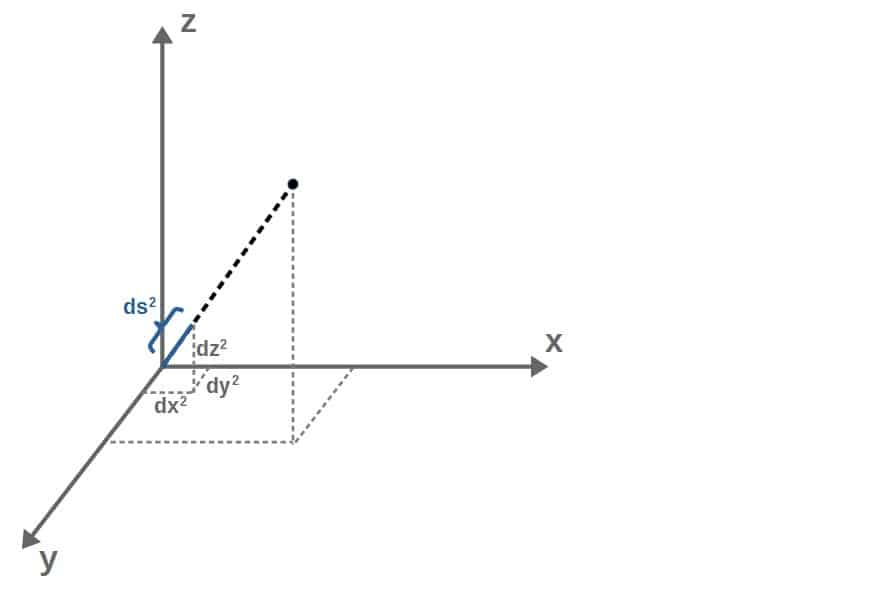
Since we’ve identified c2 as the squared size of the hypotenuse, this is our “line element“, which we’ll call ds2.
We can then treat a and b as being some small distances on an (x,y)-plane. Small changes are often written with the letter d in from of them (representing differentials), like dx and dy.
With this in mind, Pythagoras’ theorem would read:
ds^2=dx^2+dy^2This is what we call the line element in Euclidean geometry. This extends (like Pythagoras’ theorem) to three dimensions as ds2=dx2+dy2+dz2.
This line element describes a small distance in space. However, in general relativity, we model everything by describing not only space, but spacetime.
In space, we can walk forwards, backwards, turn to the side, and jump – we have motion that we can control in our three spatial dimensions. However, time acts differently. To model this, we write time slightly different in our line element as:
ds^2=-dt^2+dx^2+dy^2+dz^2This is what we call the Minkowski spacetime line element. This describes a small distance in flat spacetime. The Minkowski line element resembles a “straight line” in spacetime, meaning that there is no curvature.
If you’d like to read an intuitive introduction to special relativity, you’ll find one here. The article covers everything discussed here, but in much more detail.
The important thing for us is that the line element encodes all the information about gravity in general relativity. Minkowski spacetime is the special case where there is no gravity in our spacetime!
Much like how we economically write xµ for coordinates (worldlines), we often write the line element in a slightly different way as:
ds^2=g_{\mu\nu}dx^{\mu}dx^{\nu}The nice thing about this form of the line element is that it is completely general; we can write all line elements (even in curved spacetime) in this form.
This is also an example of index notation and Einstein’s summation convention. The rules are as follows:
- Greek letters represent the numbers 0, 1, 2, 3.
- Roman letters represent the numbers 1, 2, 3.
- If an index appears the same in an upper and lower position, we sum over all values of the index (according to rules 1 and 2).
Before we see an example of this, let’s talk about this gµν that we introduced. This is called the metric tensor. For most purposes, this is a 4×4 symmetric matrix.
To learn more about the details behind the metric tensor, check out this article. But for our purposes, right now, the metric essentially tells us the coefficients of our small distances dxµ.
The metric also describes how distances are measured in spacetime; if the spacetime is curved, the shortest distance between two points may not be a “straight” line anymore and this is all encoded in the metric!
In the Minkowski line element above, we use the special letter gµν = ηµν with:
\eta_{\mu\nu}=\begin{pmatrix}\eta_{00}&\eta_{01}&\eta_{02}&\eta_{03}\\\eta_{10}&\eta_{11}&\eta_{12}&\eta_{13}\\\eta_{20}&\eta_{21}&\eta_{22}&\eta_{23}\\\eta_{30}&\eta_{31}&\eta_{32}&\eta_{33}\end{pmatrix}=\begin{pmatrix}-1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{pmatrix}In the vocabulary of linear algebra, we say that this is a diagonal matrix and many metrics that are interesting to study are diagonal. The indices µ and ν label each entry in this matrix. Since it is diagonal, the non-zero entries are η00=-1, η11=1, η22=1 and η33=1.
With the Minkowski metric tensor as above, we can look at writing the Minkowski line element in this more compact notation. ds^2=g_{\mu\nu}dx^{\mu}dx^{\nu}=\eta_{\mu\nu}dx^{\mu}dx^{\nu}
Since we have µ and ν in both the upper and lower positions, we sum over these! But since we are only looking at diagonal matrices, this means that the only non-zero terms in the sum are when µ = ν. This then becomes:
ds^2=\eta_{\mu\nu}dx^{\mu}dx^{\nu}=\eta_{00}\left(dx^0\right)^2+\eta_{11}dx^1\left(dx^1\right)^2+\eta_{22}\left(dx^2\right)^2+\eta_{33}\left(dx^3\right)^2Our spacetime coordinates are x0=t, x1=x, x2=y and x3=z, so this becomes:
ds^2=-dt^2+dx^2+dy^2+dz^2This is the same expression as we wrote above!
Whilst having no gravity in a spacetime is the simplest case, that is not the question at hand; We want to see what happens to light in the presence of gravity!
Perhaps the most widely known spacetime with gravity (which also describes the bending of light near a star, for example) is called Schwarzschild spacetime. The Schwarzschild solution to general relativity describes how spacetime reacts to a massive, spherical object such as a star!
Before we see that, let’s recap spherical coordinates as these will be used throughout this article (and everywhere else in physics). This is the last thing we need to go over before looking at photons specifically.
Quick tip: Spherical coordinates are one of the many important things used in physics that I cover in my Advanced Math For Physics: A Complete Self-Study Course (link to the course page). In fact, vector calculus is one of most important topics you should learn for understanding relativity, electromagnetism or even just mechanics. This course will teach you that, along with giving you all the tools you need for applying everything in practice.
We can describe the position of something in space by three coordinates (x,y,z) which are great in general but become difficult if we want to think about things that are symmetric under rotations, such as a sphere (which has a radius of √(x2+y2+z2) which is often difficult to work with!).
Instead, we use spherical coordinates (r, θ, φ) which describes a radius r and two angles of rotation:
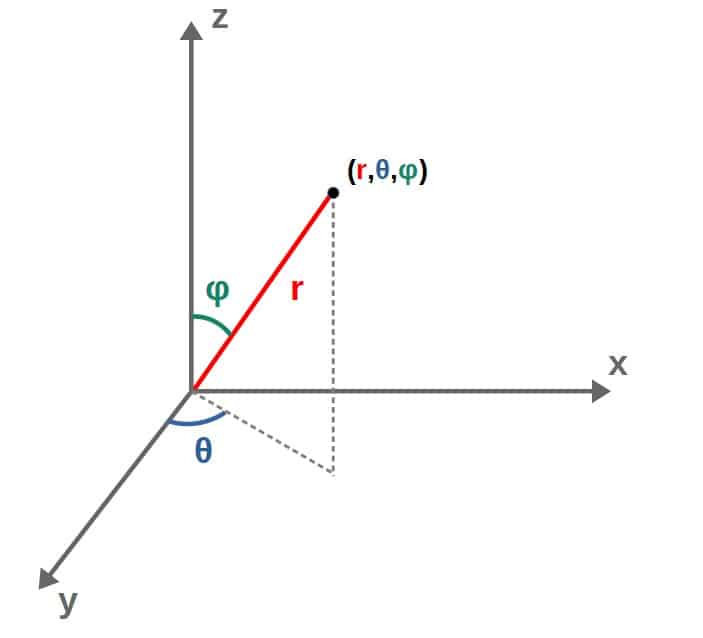
Essentially, we describe a point in space by specifying two angles and a radial coordinate (distance from the center).
In this way, spherical coordinates cover all the same space as (x, y, z) do and are equivalent but sometimes much easier to work with!
The three dimensional line element in spherical coordinates is written as:
ds^2=dr^2+r^2d\theta^2+r^2\sin^2\theta d\varphi^2In fact, this line element is equal to ds2=dx2+dy2+dz2. This signifies the fact that all distances (line elements) are the same regardless of which coordinates we describe them in; physics doesn’t care about your coordinate system!
This looks a little more complicated but despite its appearance, is much easier to work with in the case of a spherical star and in many other gravitational spacetimes as well!
Now, the line element in a Schwarzschild spacetime (which describes all distances near a gravitating spherical star) looks somewhat similar to this, but is written as:
ds^2=-\left(1-\frac{2M}{r}\right)dt^2+\frac{1}{1-\frac{2M}{r}}dr^2+r^2d\theta^2+r^2\sin^2\theta d\varphi^2M here is the mass of our star and all physical stars will have r > 2M since we look outside the star. This is relevant because 1−2M/r is zero at r = 2M. If we were modelling a non-rotating, uncharged black hole, this would correspond to the event horizon of a black hole.
The last term terms are exactly the same as the Minkowski (flat or non-gravitational spacetime) line element – this tells us that in terms of gravity, it doesn’t matter how we rotate the star, only the distance from it does.
There’s now a prefactor in front of the time portion of the line element – this is telling us that time acts differently due to gravity.
This gives us amazing features such as gravitational time dilation; we can see that the coefficient in front of dt2 gets smaller the closer we get to r = 2M, we interpret this as time slowing down!
For an interesting example on why exactly time slows down near a black hole, I have an entire article on that, which you’ll find here.
In the same manner, gravity also affects distances in the Schwarzschild spacetime. It turns out that the shortest paths for photons in Schwarzschild spacetime are actually curved trajectories, leading to the deflection of light around a star.
With line elements, metrics, and worldlines safely under our belts, we can tackle the question at hand: How does gravity affect matter? And most importantly for us, how does gravity affect photons if they have no mass?
How Does Gravity Affect The Path of a Photon?
We’ll start with one important fact: The universe is lazy. Everything – planets, photons, everything – travels on the shortest path it can.
If we consider only gravity, we want to consider the paths or worldlines that all matter follows without any external forces (since gravity is no longer a force in general relativity).
These paths have special names – geodesics! They can be assigned three different types: timelike, null and spacelike.
- Timelike geodesics are for matter that has mass and travels slower than the speed of light.
- Null geodesics are for matter without mass (such as photons) which travels at the speed of light.
- Spacelike geodesics are for matter which travels faster than the speed of light (hypothetical particles known as tachyons).
To tell us about these paths, we define the line element in a specific way since this is telling us intimate details about the geometry of our spacetime. By convention, we say:
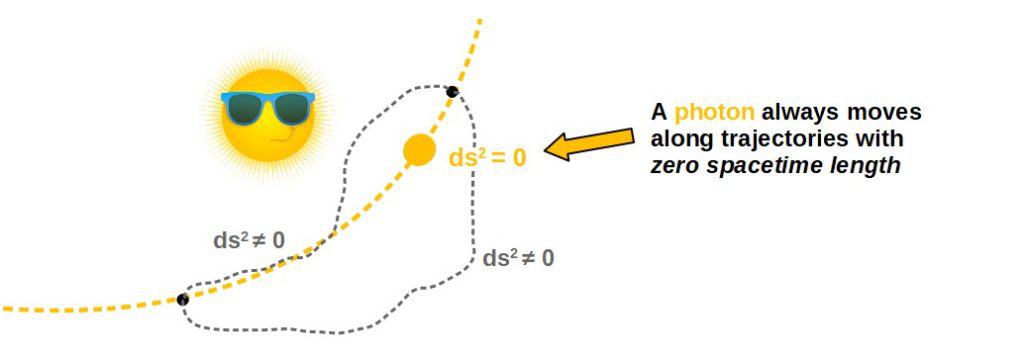
The important thing is that light travels on a null geodesic – We can now understand how gravity affects a photon by looking at these null geodesics in any given spacetime with gravity.
Let’s think about this physically for a moment: we said before that ds2 is like a distance in spacetime, so a null geodesic means that light travels on paths that have zero spacetime distance.
This sounds funny but in general relativity, this is indeed possible; a photon can still move through space without moving in spacetime (this is because of the minus sign we saw earlier in front of the dt-part of the line element).
So essentially, photons travel along the shortest paths through spacetime and at the same time, these paths always have zero spacetime length. In this sense, it doesn’t make sense to talk about a “shortest distance” in spacetime for a photon, since the spacetime distance is always zero.
In any case, photons move along null geodesics in spacetime. The shape and form of these geodesics depends on the spacetime we’re in.
Now, how do we actually find the geodesics of photons? The simplest and most brute force approach to get the trajectory is via the geodesic equation:
\frac{d^2x^{\alpha}\left(\lambda\right)}{d\lambda^2}+\Gamma_{\mu\nu}^{\alpha}\frac{dx^{\mu}\left(\lambda\right)}{d\lambda}\frac{dx^{\nu}\left(\lambda\right)}{d\lambda}=0We can see the parameterized worldlines xα(λ) in this equation that we discussed earlier appearing in three places here; the purpose of the geodesic equation is to solve for these to get the spacetime trajectories.
The first and second derivatives of the wordlines are taken in the above – these derivatives describe how the wordlines xα(λ) change as we vary the path parameter λ.
Finally, we have the Christoffel symbols, denoted by Γ. In short, these encode any changes in coordinates if we look at our system from different perspectives – just like when we changed from Cartesian (x,y,z) coordinates to spherical coordinates earlier!
For those who are interested, the Christoffel symbols are mathematically given by:
\Gamma_{\mu\nu}^{\alpha}=\frac{1}{2}g^{\alpha\beta}\left(\frac{\partial g_{\nu\beta}}{\partial x^{\mu}}+\frac{\partial g_{\mu\beta}}{\partial x^{\nu}}-\frac{\partial g_{\mu\nu}}{\partial x^{\beta}}\right)The main part we see is the metric tensor that describes our spacetime as well as its derivatives.
The Christoffel symbols give rise to phenomena such as artificial or fictitious forces like the centrifugal force when rotating something – this arises effectively from changing a coordinate system to another.
I actually have a full guide on Christoffel symbols, which you’ll find here. It covers everything from the physical and geometric meanings of the Christoffel symbols all the way up to how to actually calculate and use them in practice.
In case you’re interested to see where the geodesic equation really comes from, you’ll find its full derivation below. This uses some advanced concepts, which are presented as intuitively as possible.
In physics, the action is the object that tells us how things change and evolve. It is in the form of an integral which we call S and this is how we quantify the phrase the universe is lazy.
The path with the least action is the physical one! In general, we write it as the integral of a “Lagrangian” L – there’s a whole theory of Lagrangian mechanics and you can read about it in depth from this article here.
The action for us is called the geodesic Lagrangian. For simplicity, if a variable has a dot above it,
this represents the derivative with respect to λ. The geodesic Lagrangian is
There’s a lot of theory in the background (which you can read more about in the article linked above) but what we need is called the Euler-Lagrange equations – essentially, when the variables in the Lagrangian obey this equation, this is when the action is the least and we have a physical path!
The Euler-Lagrange equations in our case are given by:
\frac{d}{d\lambda}\frac{\partial L}{\partial\dot{x}^{\alpha}}=\frac{\partial L}{\partial x^{\alpha}}The right hand side of the equations is the easiest to deal with as we need to differentiate only once!
We can see that the Lagrangian is made up of three product terms but xα and ẋα are treated as independent variables in Lagrangian mechanics (meaning that the only thing in the Lagrangian that depends on xα is the metric gµν), so we find:
\frac{\partial L}{\partial x^{\alpha}}=\frac{\partial}{\partial x^{\alpha}}\left(\frac{1}{2}g_{\mu\nu}\dot{x}^{\mu}\dot{x}^{\nu}\right)=\frac{1}{2}\frac{\partial g_{\mu\nu}}{\partial x^{\alpha}}\dot{x}^{\mu}\dot{x}^{\nu}=\frac{1}{2}\partial_{\alpha}g_{\mu\nu}\dot{x}^{\mu}\dot{x}^{\nu}In the last equality we changed the notation for the derivative as it makes writing much more convenient!
Then, it is time to tackle the left hand side. First, we have via the product rule (note that the metric does not depend on ẋα):
\frac{\partial L}{\partial\dot{x}^{\alpha}}=\frac{\partial}{\partial\dot{x}^{\alpha}}\left(\frac{1}{2}g_{\mu\nu}\dot{x}^{\mu}\dot{x}^{\nu}\right)=\frac{1}{2}g_{\mu\nu}\frac{\partial\dot{x}^{\mu}}{\partial\dot{x}^{\alpha}}\dot{x}^{\nu}+\frac{1}{2}g_{\mu\nu}\dot{x}^{\mu}\frac{\partial\dot{x}^{\nu}}{\partial\dot{x}^{\alpha}}We can clean this up a bit! There is a mathematical rule which says that for any variable y, the following holds:
\frac{\partial y^{\mu}}{\partial y^{\alpha}}=\delta_{\alpha}^{\mu}We call this δ the Kronecker delta. It has the property of being either 0 or 1. It is 1 when µ=α and 0 otherwise. For example \delta_1^0=0 but \delta_2^2=1. For those who know some linear algebra, this is the index notation form of the identity matrix.
We can use the Kronecker delta to swap indices like this:
\delta_{\alpha}^{\mu}y^{\alpha}=y^{\mu}Combining the definition of the Kronecker delta and its index-swapping property, we get:
\frac{\partial L}{\partial\dot{x}^{\alpha}}=\frac{1}{2}g_{\mu\nu}\frac{\partial\dot{x}^{\mu}}{\partial\dot{x}^{\alpha}}\dot{x}^{\nu}+\frac{1}{2}g_{\mu\nu}\dot{x}^{\mu}\frac{\partial\dot{x}^{\nu}}{\partial\dot{x}^{\alpha}} \Rightarrow\ \ \frac{\partial L}{\partial\dot{x}^{\alpha}}=\frac{1}{2}g_{\mu\nu}\delta_{\alpha}^{\mu}\dot{x}^{\nu}+\frac{1}{2}g_{\mu\nu}\dot{x}^{\mu}\delta_{\alpha}^{\nu}=\frac{1}{2}g_{\alpha\nu}\dot{x}^{\nu}+\frac{1}{2}g_{\mu\alpha}\dot{x}^{\mu}Now, to complete the derivation, we need to take the derivative with respect to lambda of this. Both x and the metric are functions of λ – but the metric gµν is a function of x which in itself is a function of λ – we can handle this with the chain rule and product rule combined! This tells us that we can express the total derivative as:
\frac{d}{d\lambda}=\frac{dx^{\alpha}}{d\lambda}\frac{\partial}{\partial x^{\alpha}}=\dot{x}^{\alpha}\partial_{\alpha}You may have noticed that the names of Greek indices will sometimes change – this is because when they are in both the upper and lower position, they are called “dummy variables”; this means they are summed over and can really be given any name!
Before we do anything else, however, let’s use the fact that we can rename these dummy variables to write:
\frac{\partial L}{\partial\dot{x}^{\alpha}}=\frac{1}{2}g_{\alpha\nu}\dot{x}^{\nu}+\frac{1}{2}g_{\mu\alpha}\dot{x}^{\mu}=\frac{1}{2}g_{\alpha\mu}\dot{x}^{\mu}+\frac{1}{2}g_{\mu\alpha}\dot{x}^{\mu}=\frac{1}{2}\left(g_{\alpha\mu}+g_{\mu\alpha}\right)\dot{x}^{\mu}Let’s now take this final derivative with respect to λ using the product rule:
\frac{d}{d\lambda}\frac{\partial L}{\partial\dot{x}^{\alpha}}=\frac{1}{2}\frac{d}{d\lambda}\left(\left(g_{\alpha\mu}+g_{\mu\alpha}\right)\dot{x}^{\mu}\right) =\frac{1}{2}\frac{d}{d\lambda}\left(g_{\alpha\mu}+g_{\mu\alpha}\right)\dot{x}^{\mu}+\frac{1}{2}\left(g_{\alpha\mu}+g_{\mu\alpha}\right)\frac{d\dot{x}^{\mu}}{d\lambda} =\frac{1}{2}\dot{x}^{\nu}\partial_{\nu}\left(g_{\alpha\mu}+g_{\mu\alpha}\right)\dot{x}^{\mu}+g_{\alpha\mu}\frac{d\dot{x}^{\mu}}{d\lambda}In the last term we’ve used the fact that the metric is symmetric, i.e. gαµ=gµα, so that gαµ+gµα=2gαµ.
=\frac{1}{2}\left(\partial_{\mu}g_{\alpha\nu}+\partial_{\nu}g_{\mu\alpha}\right)\dot{x}^{\mu}\dot{x}^{\nu}+g_{\alpha\mu}\ddot{x}^{\mu}In the last step, we conveniently renamed our dummy variables in the first term (interchanging µ and ν as they are both dummy variables here).
Now, let’s combine the two sides of the Euler-Lagrange equation:
\frac{d}{d\lambda}\frac{\partial L}{\partial\dot{x}^{\alpha}}=\frac{\partial L}{\partial x^{\alpha}}\\\Rightarrow\ \ \frac{1}{2}\left(\partial_{\nu}g_{\alpha\mu}+\partial_{\nu}g_{\mu\alpha}\right)\dot{x}^{\mu}\dot{x}^{\nu}+g_{\alpha\mu}\ddot{x}^{\mu}=\frac{1}{2}\partial_{\alpha}g_{\mu\nu}\dot{x}^{\mu}\dot{x}^{\nu}\\\Rightarrow\ \ g_{\alpha\mu}\ddot{x}^{\mu}+\frac{1}{2}\left(\partial_{\mu}g_{\alpha\nu}+\partial_{\nu}g_{\mu\alpha}-\frac{1}{2}\partial_{\alpha}g_{\mu\nu}\right)\dot{x}^{\mu}\dot{x}^{\nu}=0There’s one more rule we need to know about that involves the “inverse metric” gαµ and it is that:
g^{\alpha\mu}g_{\alpha\nu}=\delta_{\nu}^{\mu}So if we contract (multiply) this whole equation by gασ (and use the index renaming property of the Kronecker delta), we get the result:
g^{\alpha\sigma}g_{\alpha\mu}\ddot{x}^{\mu}+\frac{1}{2}g^{\alpha\sigma}\left(\partial_{\mu}g_{\alpha\nu}+\partial_{\nu}g_{\mu\alpha}-\frac{1}{2}\partial_{\alpha}g_{\mu\nu}\right)\dot{x}^{\mu}\dot{x}^{\nu}=0\\\Rightarrow\ \ \ddot{x}^{\sigma}+\frac{1}{2}g^{\alpha\sigma}\left(\partial_{\mu}g_{\alpha\nu}+\partial_{\nu}g_{\mu\alpha}-\frac{1}{2}\partial_{\alpha}g_{\mu\nu}\right)\dot{x}^{\mu}\dot{x}^{\nu}=0The coefficients in front of these x-dots here are the Christoffel symbols! This completes our
derivation of the geodesic equation:
The key takeaway here is that the geodesic equation can be derived from a so-called geodesic Lagrangian, which means that essentially, the geodesic Lagrangian encodes the information about the geodesics in any given spacetime.
Now, in flat or Minkowski spacetime, the geodesics of photons are straight lines, just like Newton’s laws would predict. You’ll see how this comes about down below.
However, things change greatly when we consider other, more complicated spacetimes and metrics, which correspond to spacetimes in which gravity is present.
In these cases, a photon may not travel in a straight line anymore, differing from the predictions of Newtonian gravity.
The most extreme case of this may be for a photon orbiting around a black hole. I have a full article explaining how this happens, in case you’re interested.
Now, the derivative of a constant is always zero. Take for example the number 1 and think of it as a function of λ. As we change λ, the value of 1 is still 1, it doesn’t change – so we could write this mathematically as d(1)/dλ = 0.
With this in mind, take the Minkowski metric tensor; it is constant, meaning all its components are constants (either -1’s, 1’s or zeros).
This means that all the derivatives in the Christoffel symbols give us zero for the Minkowski metric, so all the Christoffel symbols are all zero too!
So, for Minkowkski spacetime ηµν (spacetime without gravity, i.e. flat spacetime), we have the geodesic equation:
\frac{d^2x^{\alpha}\left(\lambda\right)}{d\lambda^2}=0The worldline xα(λ) here consists of four different coordinates, a time coordinate t(λ) and three spacial coordinates, which we can call x(λ), y(λ) and z(λ). These are all functions of the path parameter λ.
Looking at the geodesic equation component-by-component, we see that:
\frac{d^2t}{d\lambda^2}=0\ {,}\ \ \frac{d^2x}{d\lambda^2}=0\ {,}\ \ \frac{d^2y}{d\lambda^2}=0\ {,}\ \ \frac{d^2z}{d\lambda^2}=0We can solve all these quite simply by integrating twice (don’t worry if you don’t know quite what that means!). Let’s also assume that our worldline xα is along the x-axis with y = 0 and z = 0. Doing this, one solution is:
t=\lambda\ {,}\ \ \ x=v\lambda+x_0Here, x0 is defined as the starting position of the worldline at λ = 0 and v (a constant) is the derivative of x, corresponding to a constant velocity.
Since we have t = λ here (meaning that physically, the path parameter is simply time in this simple example), we can combine these two equations into one:
x=vt+x_0This is motion in a straight line. Keep following me – if we take the second derivative with respect to time, we would write:
\frac{d^2x}{dt^2}=0What is the relevancy of this? Well, the rate of change of position x(t) is the velocity v(t) and the rate of change of velocity is acceleration, so we have:
\frac{d^2x}{dt^2}=a=0For real matter, it has either a mass of zero (for example light) or a positive mass (like you and me). Let’s call this mass m. Since a is always zero, we can just multiply it by m and it doesn’t change anything. We would then have:
ma=0This is Newton’s second law for a body under no external force! Wonderful – the framework of general
relativity allows us to even include Newtonian physics!
The physical relevancy of this is that under no gravity (in flat or Minkowski spacetime), photons travel along straight lines, under no gravitational or any other forces.
As we’ve seen, the geodesic equation in specific circumstances can tell us all about Newtonian physics but it can do much more.
For any spacetime, if you can write down its metric, you can plug it into the geodesic equation and find the equations of motion for any particle! However, that doesn’t mean the equation is always necessarily solvable, but if it is, then you can find the trajectories of a photon (or any other particle) under gravity.
Mathematically, a more elegant approach is to take the metric, look at its geodesic Lagrangian (explained earlier), calculate its Euler-Lagrange equations, and combine this with the fact that we are looking at null geodesics for light!
We can easily get the geodesic Lagrangian by taking the line element, replacing any variable (such as dt, dr, dx etc.) by the same variable with a dot over it (ṫ, ṙ, ẋ etc.), representing a derivative with respect to λ and putting a half in front of the whole thing!
For example, in the Schwarzschild spacetime we briefly looked at earlier, we have (see the similarity between the line element and the geodesic Lagrangian?):
ds^2=-\left(1-\frac{2M}{r}\right)dt^2+\frac{1}{1-\frac{2M}{r}}dr^2+r^2d\theta^2+r^2\sin^2\theta d\varphi^2In fact, this can also be used as an efficient method for calculating Christoffel symbols. I cover this “trick” in this article.
Now, to answer the main question: if photons are massless, how are they affected by gravity – under the influence of gravity, photons travel on null geodesics (ds2 = 0) and geodesics are described by the Euler-Lagrange equations of their geodesic Lagrangian (or equivalently by the geodesic equation; both describe the same thing).
The equations we get are determined by the metric gµν and in general relativity, gravity is the curving of spacetime rather than a force so all the effects of gravity are wrapped up in the metric.
Photons, like all matter, want to follow a geodesic because of the laziness of the universe and the easiest path to take is to follow how matter has bent and curved spacetime, causing gravity.
The point is that it doesn’t matter whether the photons are massless or not; they still travel along geodesics and IF the metric describes a curved spacetime (in which gravity is present), then the photons will inevitably move along curved paths as well. This is how gravity affects photons!
The only place where the fact that photons are massless actually matters is that the geodesics of photons are null (ds2 = 0), which is different in the case for massive particles (with ds2 = -1 instead).
This doesn’t change the fact that photons are still affected by gravity, it simply causes the paths of photons and massive particles to look slightly different.
For example, light can orbit a black hole at only one possible distance, while a massive particle could have two different orbits. You can read more about orbits of light around a black hole in this article.
With all this theory, let’s see it altogether fully in an example spacetime!
How Gravity Affects Photons Near a Star
We have seen already that in the presence of no external forces and without gravity, all matter travels in straight lines. If we introduce gravity, that is no longer true – think about planetary orbits!
Let’s look at what happens to a photon (light) when it passes a perfectly spherical star. In Newtonian gravity, we would expect for the photons to keep moving in a straight line, as gravity does not affect them.
In general relativity, this is not true – the key result is that a ray of light passing a star gets deflected by an angle:
\delta=\frac{4GM}{c^2D}G is the gravitational constant, c is the speed of light, M is the mass of the star, and D is the smallest distance radially that the light gets to the star.
Essentially, this deflection angle describes how much a light ray would get bent as it passes near a star. In other words, how much the path of the photon differs from being a straight line.
This can be observed by looking at light rays (photons) coming from a distant star – since the light rays get deflected as they pass the Sun, for us, the distant star would appear to be in a different position in the sky compared to where we would expect it to be.
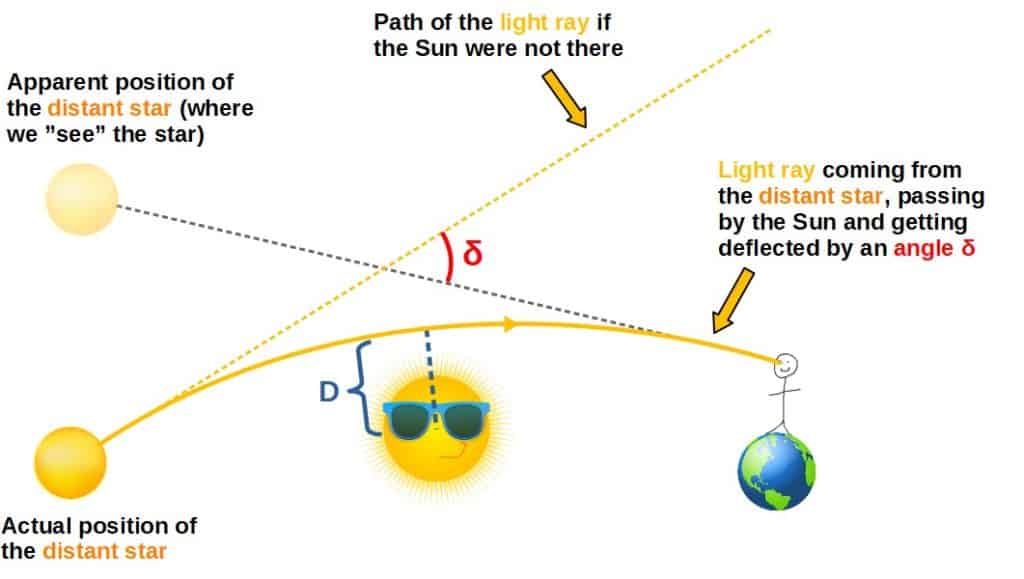
For some context, if we consider light just grazing the sun, this gives a measurement of 1.75 arcseconds – Arthur Eddington verified this empirically in 1919 and it was a key result in verifying general relativity experimentally!
The deflection angle δ is typically very small. For scale, an arcsecond is 1/3600th of a degree – so the result is very very small as expected – but crucially it is not zero as we would expect in Newtonian gravity!
This shows directly how a massless photon is affected by gravity – it must follow the natural bending of spacetime due to matter!
Now, where does this result come from? Let’s get down to the details – the key ingredient is geometry!
Essentially, we will discover that the geodesic of a photon as it passes by a star, is described by the following equation:
r\left(\varphi\right)=\frac{D^2}{M}\frac{1}{1+C\cos\varphi+\frac{D}{M}\sin\varphi+\cos^2\varphi}Note; this is in units where G=c=1. In case you’re familiar with standard orbital mechanics, this may look somewhat similar to Kepler’s orbit equation describing, for example, the elliptical orbits of planets. In a sense, this is a more complicated “orbit equation” that describes the orbit of a photon.
This describes the distance r of the photon to the star as a function of the angle φ in polar coordinates (see picture below).
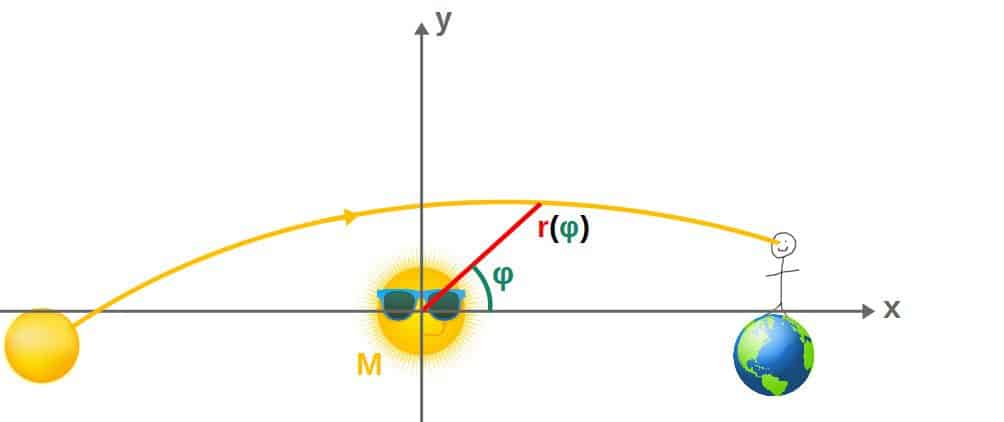
From this, we can derive the deflection angle δ=4GM/c2D. You’ll see the full derivation of this below.
We begin with the Schwarzschild metric and its geodesic Lagrangian from earlier:
ds^2=-\left(1-\frac{2M}{r}\right)dt^2+\frac{1}{1-\frac{2M}{r}}dr^2+r^2d\theta^2+r^2\sin^2\theta d\varphi^2 L=-\frac{1}{2}\left(1-\frac{2M}{r}\right)\dot{t}^2+\frac{1}{2}\frac{1}{1-\frac{2M}{r}}\dot{r}^2+\frac{1}{2}r^2\dot{\theta}^2+\frac{1}{2}r^2\sin^2\theta\dot{\varphi}^2This metric and its associated geodesic Lagrangian describes gravity outside of any spherically symmetric, non-rotating, uncharged mass M. This gives us a great model of a star like the Sun!
We’ll be looking at geodesics, which are the shortest distance between two points. If we traced out these lines, we’d find that each individual one stays on one plane – it doesn’t wiggle around in three spatial dimensions since this wouldn’t be the shortest path anymore.
We are then free to choose this plane and due to spherical symmetry (if we rotate our spacetime around the star it looks the same) we can choose, for example, the plane θ = π/2 as this simplifies our geodesic Lagrangian in the following way:
L=-\frac{1}{2}\left(1-\frac{2M}{r}\right)\dot{t}^2+\frac{1}{2}\frac{1}{1-\frac{2M}{r}}\dot{r}^2+\frac{1}{2}r^2\dot{\varphi}^2This follows because θ is now a constant and we know the derivative of a constant is zero, hence θ-dot = 0 and also
sin(π/2) = 1.
In the language of Lagrangian mechanics, we treat variables with dots above them and variables without dots above them as independent. We can see that the coefficients of each of the dotted variables in the geodesic Lagrangian only depend on r. This means that any derivative of L with respect to t or φ would be zero – we call these variables cyclic coordinates.
In action, that means:
\frac{d}{d\lambda}\frac{\partial L}{\partial\dot{t}}=\frac{\partial L}{\partial t}=0 \frac{d}{d\lambda}\frac{\partial L}{\partial\dot{\varphi}}=\frac{\partial L}{\partial\varphi}=0If the derivative of something is zero – this is the λ-derivative for us – then this means the thing we’re differentiating is constant. We can name these constants in nice ways as -E and L (not to be confused with the Lagrangian), so that:
\frac{\partial L}{\partial\dot{t}}=-\left(1-\frac{2M}{r}\right)\dot{t}=-E \frac{\partial L}{\partial\dot{\varphi}}=r^2\dot{\varphi}=LThe letters E and L may seem familiar, they’re often used to denote energy and angular momentum. This is physically motivated by the fact that these cyclic coordinates relate exactly to the conservation of energy and angular momentum in our spacetime.
We can arrange these equations to give us:
\dot{t}=\frac{E}{1-\frac{2M}{r}} \dot{\varphi}=\frac{L}{r^2}What we’ve done so far isn’t yet specific to us considering a photon on a null geodesic. We get that by remembering that a null geodesic has zero spacetime length, which is rendered mathematically by setting the metric line element to zero:
-\left(1-\frac{2M}{r}\right)dt^2+\frac{1}{1-\frac{2M}{r}}dr^2+r^2d\varphi^2=0We can manipulate our equations for t-dot and φ-dot. Recalling, we have:
\dot{t}=\frac{dt}{d\lambda}=\frac{E}{1-\frac{2M}{r}}\ \ \Rightarrow\ \ dt=\frac{E}{1-\frac{2M}{r}}d\lambda \dot{\varphi}=\frac{d\varphi}{d\lambda}=\frac{L}{r^2}\ \ \Rightarrow\ \ d\varphi=\frac{L}{r^2}d\lambdaLet’s plug these into our null geodesic line element!
-\left(1-\frac{2M}{r}\right)\left(\frac{E}{1-\frac{2M}{r}}d\lambda\right)^2+\frac{1}{1-\frac{2M}{r}}dr^2+r^2\left(\frac{L}{r^2}d\lambda\right)^2=0\\\Rightarrow\ \ -\frac{E^2}{1-\frac{2M}{r}}d\lambda^2+\frac{1}{1-\frac{2M}{r}}dr^2+\frac{L^2}{r^2}d\lambda^2=0If we divide by dλ2 and multiply by (1−2M/r), we get:
-E^2+\dot{r}^2+\frac{L^2}{r^2}\left(1-\frac{2M}{r}\right)=0A common way of writing this is as:
\frac{1}{2}\dot{r}^2+V_{eff}\left(r\right)=\frac{1}{2}E^2\ {,}\ \ V_{eff}\left(r\right)=\frac{L^2}{2r^2}\left(1-\frac{2M}{r}\right)=\frac{L^2}{2r^2}-\frac{ML^2}{r^3}Here, Veff stands for “effective potential”. The effective potential is a common tool used in orbital mechanics to study orbits of objects. This particular effective potential can even be used to analyze orbits of light around a black hole (which you can read more about here).
This equation essentially has the form of kinetic energy + potential energy = constant. This geodesic equation is just the equation describing a particle of mass m=1 and energy E2/2 in a potential Veff(r)!
Now, getting back to the main topic at hand, how a photon is affected by gravity and how light
is bent by gravity, we want to consider the geodesic motion of a photon, so let’s first write our above equation in the following form:
Then, consider the following expression:
\frac{\dot{r}^2}{\dot{\varphi}^2}=\frac{\left(\frac{dr}{d\lambda}\right)^2}{\left(\frac{d\varphi}{d\lambda}\right)^2}=\left(\frac{dr}{d\varphi}\right)^2=\frac{E^2-\frac{L^2}{r^2}\left(1-\frac{2M}{r}\right)}{\frac{L^2}{r^4}}\\\Rightarrow\ \ \left(\frac{dr}{d\varphi}\right)^2=\frac{E^2}{L^2}r^4-r^2\left(1-\frac{2M}{r}\right)This is now a differential equation describing r as a function of φ. Solving these types of equations falls within the topic of “orbital mechanics” and it is very common to use the change of variables u=1/r – this is because we have 1/r everywhere in our equations and it is easier if they were flipped!
We treat r as a function of φ and so u is also as a function of φ. In our main expression we have dr/dφ, but after our variable change r=1/u, so this will change (using the chain rule) like this:
\frac{dr}{d\varphi}=\frac{d}{d\varphi}u^{-1}=-\frac{1}{u^2}\frac{du}{d\varphi}Let’s plug this and u=1/r into our equation above:
\left(\frac{dr}{d\varphi}\right)^2=\frac{E^2}{L^2}r^4-r^2\left(1-\frac{2M}{r}\right)\\\Rightarrow\ \ \left(-\frac{1}{u^2}\frac{du}{d\varphi}\right)^2=\frac{E^2}{L^2}\frac{1}{u^4}-\frac{1}{u^2}\left(1-2Mu\right)\\\Rightarrow\ \ \frac{1}{u^4}\left(\frac{du}{d\varphi}\right)^2=\frac{E^2}{L^2}\frac{1}{u^4}-\frac{1}{u^2}\left(1-2Mu\right)Now let’s multiply by u4 and we are left with:
\left(\frac{du}{d\varphi}\right)^2=\frac{E^2}{L^2}-u^2\left(1-2Mu\right)This expression isn’t very easy to work with at all, so we use a clever trick – we’ll take the φ-derivative of the whole expression (with the aid of the chain rule). The left and right hand sides of this equation become:
\frac{d}{d\varphi}\left(\frac{du}{d\varphi}\right)^2=\frac{d}{d\varphi}\left(\frac{E^2}{L^2}-u^2\left(1-2Mu\right)\right)\\\Rightarrow\ \ 2\frac{du}{d\varphi}\frac{d^2u}{d\varphi^2}=-2u\frac{du}{d\varphi}+6Mu^2\frac{du}{d\varphi}We can safely assume that du/dφ ≠ 0. Why? Well, if we assume that it does equal zero, then we find u=constant, and so r=constant. This is just the equation of a circular orbit (if the radius doesn’t change, it must be a circle) and around a star, light cannot have circular orbit (only around a black hole, it can)!
Now, we can safely divide by 2du/dφ and we recover (after some rearranging):
\frac{d^2u}{d\varphi^2}+u=3Mu^2This is the key orbital equation we need, which describes the motion of a photon near a star.
We can now find an approximate solution to this equation. The reason we do this is because Mu2 is very small for a star. Therefore, an approximate solution is enough to describe the geodesics of light near a star perfectly well.
The trick to solving the above differential equation is to consider it in two “parts” – we first solve it in the case where there is no gravity and then add corrections to it, representing what happens in the case WITH gravity (these “gravitational corrections” can be assumed as somewhat weak, however!).
Now, since u=1/r, this is related to how close to the center of the star we can get. It is a fact that the radius of a star is greater than 2M (the star’s Schwarzschild radius) – otherwise our metric would break down!
Even if we look at r=2M, this means u2=1/4M2, so Mu2=1/4M. But M is the mass of the star which is massive! So 1/M is tiny – so small in fact that we will start our approximation by ignoring it, which turns out to give us the “first part” of our solution; we now solve the following equation:
\frac{d^2u}{d\varphi^2}+u=0This is the equation we get if we set M = 0 as well – this is the zero gravity orbital equation. It has another name: the simple harmonic motion equation and fortunately has a nice solution! All its solutions look like waves and can be written as:
u=\frac{1}{D}\sin\left(\varphi-\varphi_0\right)D and φ0 here are just some arbitrary constants that appear when we solve this equation by integration.
D, however, has some physical meaning for us – recall that since u=1/r , then D=r sin(φ − φ0). But in polar coordinates, we have y=r sin(φ) – this tells us that D is the vertical distance from a purely radial ray:
Not only does D have physical meaning but we can interpret this entire solution as the whole straight line a distance D from a purely radial ray. A straight line is exactly what we’d expect if there were zero gravity!
Now, with this “no-gravity solution” in our hands, let’s try to obtain the full equation (with the “gravitational part” as well)!
If we call our initial solution u0 (with no gravity), so that:
u_0=\frac{1}{D}\sin\left(\varphi-\varphi_0\right)Then, we can look for a “full” solution of the form u=u0+u1 where we assume u1 is some correction (smaller than u0) to the straight line solution that describes the effects of gravity on the photon’s path.
To tidy up the math a bit, let’s write our assumption as u=u0+3Mu1 (we can always just “guess” a solution of this form, since we don’t know what u1 is yet). The full differential equation is:
\frac{d^2u}{d\varphi^2}+u=3Mu^2If we plug in our guess for u and ignore terms of the form (Mu)2 since these would be very very small, then we have:
\frac{d^2}{d\varphi^2}\left(u_0+3Mu_1\right)+u_0+3Mu_1=3M\left(u_0+3Mu_1\right)^2\\\Rightarrow\ \ \frac{d^2u_0}{d\varphi^2}+u_0+3M\frac{d^2u_1}{d\varphi^2}+3Mu_1=3Mu_0^2+18M^2u_0u_1+27M^3u_1^2In our approximation, any of the terms with M2 or M3 drop out, since these are very very small. Hence we ignore them and we then have:
\frac{d^2u_0}{d\varphi^2}+u_0+3M\frac{d^2u_1}{d\varphi^2}+3Mu_1=3Mu_0^2But, u0 is a solution to:
\frac{d^2u_0}{d\varphi^2}+u_0=0This is exactly the first two terms on the left-hand side, which must be zero so we can substitute that into the above and get (also cancelling out the 3M-factors):
\frac{d^2u_1}{d\varphi^2}+u_1=u_0^2The nice thing now is that we know u0 in terms of φ – this is now a differential equation we can solve for u1 as well!
So, u0=sin(φ − φ0)/D, but since φ0 is pretty arbitrary, we can simply assume φ0=0 (this wouldn’t change our results) to simplify this a bit. This then gives us the equation:
\frac{d^2u_1}{d\varphi^2}+u_1=\frac{\sin^2\varphi}{D^2}This equation is very close to the simple harmonic motion equation but with a non-zero term on the right hand side. We can solve this equation using the theory of “ordinary 2nd order constant-coefficient inhomogeneous differential equations”, which sounds fancy but in reality is just using smart guesses to find a solution!
Within the differential equations framework, this is quite a routine calculation and the resulting solution is:
u_1=\frac{1+C\cos\varphi+\cos^2\varphi}{3D^2}C is again one of these arbitrary integration constants we’ve mentioned that comes up in the calculation. You can verify that this solution works simply by plugging it into the differential equation above and see that it indeed satisfies it.
Now we see that u1 is indeed small – the 1/D2 is smaller than 1/M2 which is very tiny! Let’s put everything together now. Our full solution for u is:
u=u_0+3Mu_1\\\Rightarrow\ \ u=\frac{\sin\varphi}{D}+\frac{M}{D^2}\left(1+C\cos\varphi+\cos^2\varphi\right)This is the approximate solution describing the geodesics of light passing by a star! The second term in our solution is much smaller than the first (since D is really big) so the path that the light takes really is only a small deviation from a straight line.
If you want to, you can put this in terms of the original variable, r, by plugging in u=1/r. This results in:
r=\frac{1}{\frac{\sin\varphi}{D}+\frac{M}{D^2}\left(1+C\cos\varphi+\cos^2\varphi\right)}=\frac{D^2}{M}\frac{1}{1+C\cos\varphi+\frac{D}{M}\sin\varphi+\cos^2\varphi}Now, here comes the geometry part – let’s calculate the angle of deflection. First, we know that at large r, u gets very small. Far away from the star – assuming there’s nothing else close by – the light will be effectively travelling on a straight line since the effect of the star will be very weak when far away.
Let’s choose the angles that the light comes in and leaves to be −ε1 and π+ε2, like in this diagram:
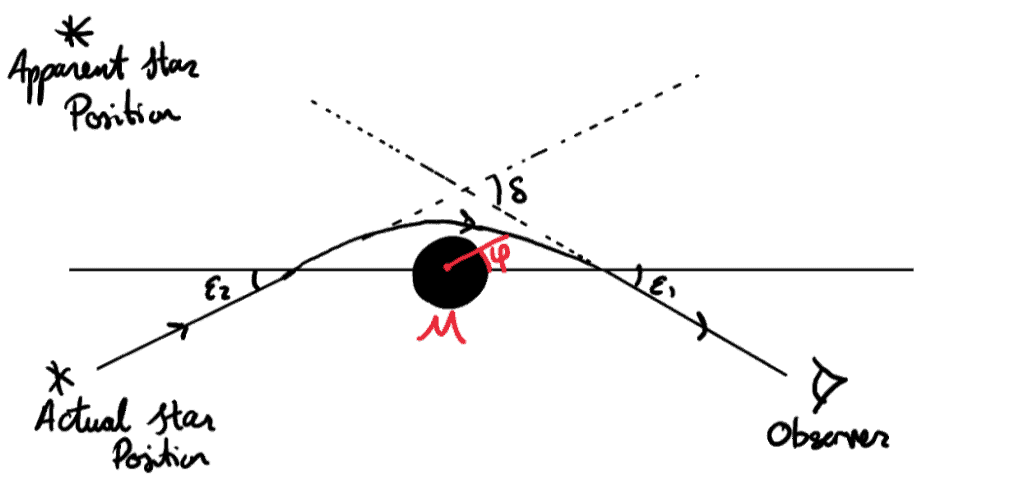
The figure isn’t quite drawn to scale, as otherwise we wouldn’t be able to see the important details on it, but it represents the path of the light that we’re considering. On this diagram, the angle that the light gets deflected is called δ. This is the change in the actual position of the star versus where we perceive the star!
We know that this effect is small so ε1 and ε2 are both very small too. Since these are angles, we want to plug these in to our solution u(φ).
These angles represent what angle the light is when really far away from the star – far away, u is approximately zero (since r is really big and u=1/r is really small). On one hand, at φ=π+ε2 with u≈0, we have:
u\left(\pi+\varepsilon_2\right)=\frac{\sin\left(\pi+\varepsilon_2\right)}{D}+\frac{M}{D^2}\left(1+C\cos\left(\pi+\varepsilon_2\right)+\cos^2\left(\pi+\varepsilon_2\right)\right)=0This isn’t the easiest to deal with, however, we have two things to help us. First, the relations sin(x + π) = − sin(x) and cos(x + π) = -cos(x). These come from the fact that if you take the cosine or sine graph and translate it across by π-units, you find the same graph but upside down – i.e. (−1) times the original graph.
Secondly, we have the “small angle approximations”. These allow us to approximate with good accuracy what a trigonometric function is without calculating it – so long as the angle is small!
If ε represents a small angle, then we can approximately write sin(ε) = ε and cos(ε) = 1. Using all of this, we can write our expression as:
\frac{-\sin\left(\varepsilon_2\right)}{D}+\frac{M}{D^2}\left(1+C\cos\left(\varepsilon_2\right)+\cos^2\left(\varepsilon_2\right)\right)=0\\\Rightarrow\ \ -\frac{\varepsilon_2}{D}+\frac{M}{D^2}\left(1-C+1\right)=0\\\Rightarrow\ \ -\varepsilon_2+\frac{M}{D}\left(2-C\right)=0Looking now at the other angle, φ=−ε1 (again with u≈0 and with the same trigonometric “tricks”), we have:
\frac{\sin\left(-\varepsilon_1\right)}{D}+\frac{M}{D^2}\left(1+C\cos\left(-\varepsilon_1\right)+\cos^2\left(-\varepsilon_1\right)\right)=0\\\Rightarrow\ \ -\varepsilon_1+\frac{M}{D}\left(2+C\right)=0We now have two very similar equations and both equal zero – let’s add them together!
-\varepsilon_2+\frac{M}{D}\left(2-C\right)-\varepsilon_1+\frac{M}{D}\left(2+C\right)=0\ \ \Rightarrow\ \ \varepsilon_1+\varepsilon_2=\frac{4M}{D}We can see that the arbitrary constant C had no physical meaning in terms of our problem, so it cancelled out of our equation.
Now we just need to figure out what ε1+ε2 means in relation to our deflection angle, the thing we want to calculate.
By drawing two parallel lines to our horizontal line in the previous diagram, we can write the straight line trajectories as:
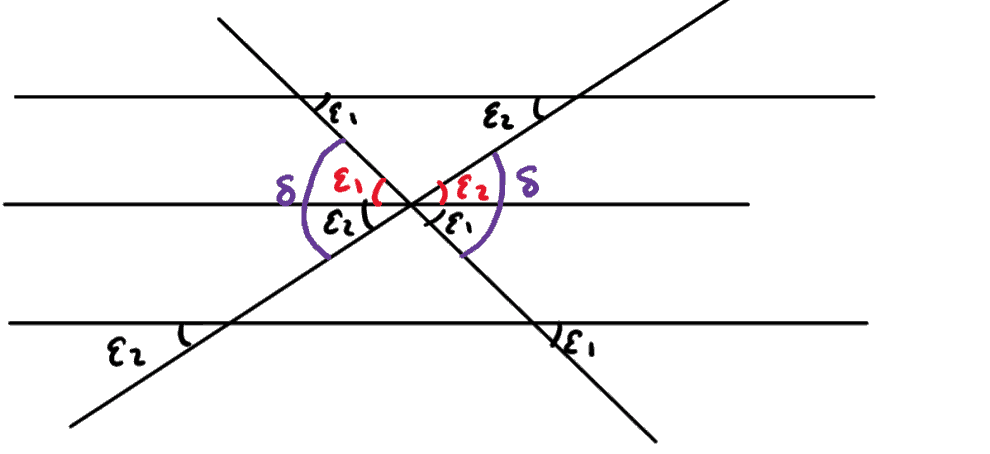
How do we read this? The bottom horizontal line is our original line (the x-axis, essentially) and the two crossed lines are the straight lines we draw at angles −ε1 and ε2+π.
Here we have two types of angles since there are intersections of parallel lines – Z angles and F angles (also called corresponding angles and alternate angles).
These tell us which angles are the same and in this diagram the corresponding
angles (F angles) are in black and alternate angles in red from the top two ε1 and ε2.
We can also see the deflection angle δ marked on this diagram. The main point here is that from this, we can read the result δ=ε1+ε2. This is the link we needed!
We can now conclude that the full deflection angle is:
\delta=\varepsilon_1+\varepsilon_2=\frac{4M}{D}However, in physics it is often convenient to set the constants G=1 and c=1 (as is done here) because we can always check the dimensions later and restore them. Let’s restore these back in, giving the promised result δ = 4GM/c2D.
More importantly than the actual result of deflection, this is an example that directly shows that photons are indeed affected by gravity – how they are affected by gravity will depend on the particular spacetime we look at.
In Minkowski spacetime, we saw that photons travel in straight lines. This corresponds to the case with no gravity and is consistent with what we expect in Newtonian physics!
However, in Schwarzschild spacetime (under the gravity of a spherical mass), a photon will travel in a curved path and get deflected. In this case, the photon will be affected by gravity.
In other spacetimes, photons will also generally be affected by gravity but in different ways – near a rotating black hole (described by the so-called Kerr spacetime), for example, a photon’s trajectory may look incredibly complicated.
