Why Do Photons Not Have Mass? (Simple Proof)

Photons, which are essentially light particles or more accurately, the quanta of electromagnetic fields, are often described as having no mass, but why exactly is this the case? Why do photons have no mass?

In short, the special theory of relativity predicts that photons do not have mass simply because they travel at the speed of light. This is also backed up by the theory of quantum electrodynamics, which predicts that photons cannot have mass as a result of U(1) -gauge symmetry.

Now, to fully understand this, we have to go a little bit deeper into the theory behind photons. Later, I’ll also explain some ways the mass of a photon could actually be measured and why experimental evidence also seems to agree with the theoretical predictions.

Intuitively, Why Can’t Photons Have Mass?

First of all, let’s think about what mass actually means. In a modern sense, mass is defined as the energy a particle has at rest (i.e. rest energy). This is actually a fundamental prediction of Einstein’s special relativity, described by the energy-momentum relation:

E=\sqrt{p^2c^2+m^2c^4}

This equation states that the total energy (E) of a particle is given in terms of its momentum (p) and its mass (m). This is, however, only valid for a particle which has no potential energy.

If the particle is at rest, it has zero momentum (p=0) and we get for the energy:

E=mc^2

This is, of course, the famous equation E=mc², however, it highlights an important point; mass is simply another form of energy, namely, the energy that any particle has at rest. This IS the fundamental definition of mass.

Based on this, we can also intuitively reason why a photon does not have mass and it comes from another prediction of special relativity. Namely, the fact that a photon always travels at the speed of light c.

And by this, I really mean always; a photon cannot be brought to rest. To be technical, it cannot be brought to rest in a vacuum (which is the important part here).

Inside a material, there are other mechanisms at play (in a superconductor, a photon actually behaves as if it had mass), but these won’t be important for us. The important property is the rest energy in a vacuum, since this is how the mass of a particle is defined in a universal sense.

Now, since the photon cannot be at rest in a vacuum, it’s impossible to actually measure the rest energy of a photon. I mean, how do you measure the property of something at rest if it cannot be at rest?

This hints to the fact that maybe photons don’t actually have rest energy at all, since it isn’t defined in any reasonable sense. This would then mean that photons do not have mass either, since mass is practically defined as rest energy.

Now, of course this isn’t really a proof of anything, it is simply a way to intuitively see why it could make sense that photons don’t have mass.

How Does Special Relativity Predict That Photons Have No Mass? (Simple Mathematical Proof)

One of the consequences of Einstein’s theory of special relativity is that particles which move at the speed of light (c), can’t have any mass. Or another way to say it is that particles with mass can’t move at the speed of light.

For photons, which of course move at the speed of light, this prediction indeed happens to be true. But how exactly does special relativity predict this?

The answer is very simple and to see it, you only need one of the fundamental results of special relativity, which is the formula for relativistic total energy:

E=\frac{mc^2}{\sqrt{1-\frac{v^2}{c^2}}}

If you are not familiar where this comes from or are interested in it, I’d recommend reading my special relativity article.

From this, you simply solve for the mass and see what happens in the case of a photon (i.e. when the velocity v is the speed of light c):

m=\frac{E}{c^2}\sqrt{1-\frac{v^2}{c^2}}

Now, if we set the velocity v equal to the speed of light c, this gives the mass equal to zero:

m=\frac{E}{c^2}\sqrt{1-\frac{c^2}{c^2}}=\frac{E}{c^2}\sqrt{1-1}=0

I should also make clear that this prediction simply tells you what the mass of a particle travelling at c should be. The above equation doesn’t mean that the mass somehow changes at different speeds, it simply just describes what the mass of a particle with given energy E and given velocity v has to be.

This simple prediction applies to all particles which move at the speed of light, such as gravitons (hypothetical particles that are predicted to be the gauge bosons of gravitational fields) and gluons (although it’s kind of difficult to experimentally verify this, since gluons are never found by themselves).

Also, it’s worthwhile to say that this fact works the same way around. If a particle doesn’t have mass, it must always move at the speed of light.

How Quantum Field Theory Requires Photons To Have No Mass

There is also a more fundamental way to explain why photons don’t have mass, which is that it is simply a requirement of quantum field theory, or more accurately, quantum electrodynamics (QED).

Now, this really is the most fundamental way to explain the mass of photons, because quantum field theory is the single most accurate theory of nature that we have. To really understand how this relates to photons and their mass, we’ll have to talk a little bit about quantum field theory and QED.

What Is Quantum Electrodynamics and How Does It Relate To The Mass of a Photon?

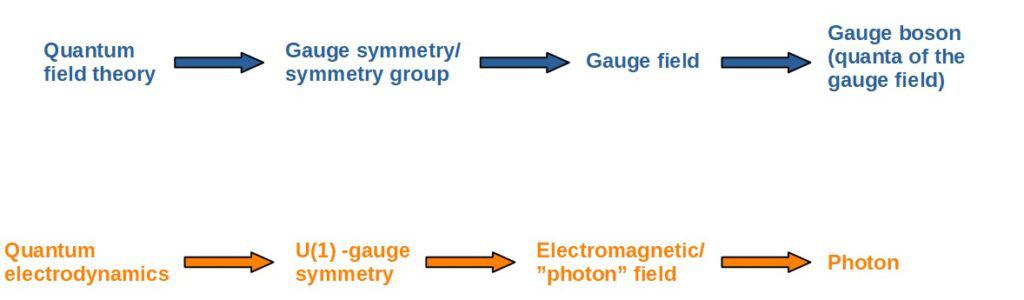
First of all, quantum field theories are a class of theories that describe different physics by using what are called quantum fields. The quantum field theory related to photons (and electromagnetism) is called quantum electrodynamics.

Now, what exactly are quantum fields anyway? Essentially, the defining features for most quantum field theories are more or less the following:

• A quantum field, in a simple sense, is a field whose excitations correspond to what we typically call particles (an excitation simply means that the field is in a higher energy state than the vacuum energy).

• Quantum field theories (in the Standard Model) are gauge theories. This means that each quantum field theory has certain symmetries associated with it, called gauge symmetries. The specific forms of symmetries for a given theory form a symmetry group.

• At a very high level, a gauge symmetry in a quantum field theory means that it’s possible to have different mathematical expressions of a given field without actually changing any of the properties or dynamics of that field.

• Gauge symmetries give rise to gauge fields. These gauge fields are what describe the interactions between different particles (i.e. the fundamental forces of nature).

• The quanta (excitations i.e. particles) of these gauge fields are called gauge bosons. So, these gauge bosons are the “exchange particles” for the different fundamental forces.

Now, in the case of quantum electrodynamics, it is a gauge theory with the symmetry group U(1). This U(1)-group (which also gives rise to conservation of electric charge) also has a gauge field associated with it, which is the electromagnetic field (well, technically it is the vector potential of the EM-field).

The quanta of this gauge field, which is the “exchange” particle of electromagnetic forces, is called the photon.

Well, great, we now know what a photon is, but what does any of this have to do with the photon not having any mass? The defining property here is that a photon is classified as a gauge boson.

It actually turns out that mathematically, there is no way to add a mass term for the photon without breaking gauge symmetry, which is what the whole Standard Model is practically based on.

Other gauge bosons (such as the W and Z bosons) can, however, obtain a mass regardless through something called spontaneous symmetry breaking and the Higgs field, but this does not occur for the photon.

So, in fact, the quantum field theoretical explanation for why a photon does not have mass is that gauge symmetry forbids it.

Therefore, if we want quantum electrodynamics to work like it should and also agree with experiments, the photon cannot have a mass (this is quite an important point as all experimental evidence also suggests the photon to be massless).

In any case, it’s still possible to “pretend” that the photon could get a mass from the Higgs mechanism and construct theories where the photon does have a mass.

Even though these lead to some very interesting consequences in, for example electromagnetism (for massive photons, electromagnetic waves should have three polarization states), they simply do not correspond to reality or anything that has been experimentally verified (apart from the superconducting phenomenon, which is a whole other story).

Is There Any Experimental Evidence That Photons Don’t Have Mass?

When we’re talking about experimental evidence, there are always limitations and inaccuracy to every measurement, which ultimately comes from the fact that nothing can be measured infinitely precisely.

In the case of the mass of a photon, it’s not really possible to measure it as exactly zero. After all, how do you measure something that doesn’t exist (there are also quantum effects taking place, which place limits on the possible accuracy of experiments)?

The best we can do is place upper limits on the photon’s mass, which has been done to a very high degree of accuracy.

Now, it’s worth noting that these upper limits are generally very tiny numbers, extremely close to zero. This of course indicates that the mass of a photon is also extremely small (it could likely be proven to be exactly zero, if it was possible to measure it accurately enough).

The simplest way to measure the mass of a photon is to measure electric fields produced by charged particles.

It turns out that if the photon had a mass, it would change the way electric fields behave (after all, the photon can be thought of as the “exchange” particle of electric forces).

Namely, the equation for an electric field produced by a charge Q (essentially Coulomb’s law) would have some extra terms in it:

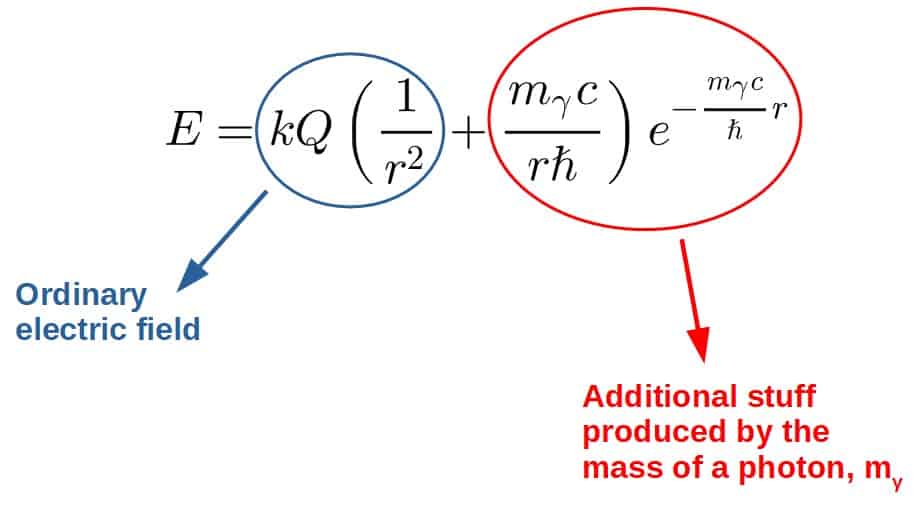
These electric fields can, of course, be observed and by measuring these so-called “damping factors” produced by the photon’s mass, it is possible to deduce an upper limit for the mass of a photon.

These experiments have provided an upper limit ranging from 10^-42 to 8×10^-51 kg for the photon’s mass, depending on the type of experiment done (according to a publication from the Huazhong University of Science and Technology).

There are even methods for measuring the mass of a photon that involve measurements of planetary magnetic fields.

One of these experiments, by using data from the Pioneer 10 spacecraft flying by Jupiter, measured an upper limit of 7×10^-52 kg on the photon mass (source: review by the C.N. Yang Institute for Theoretical Physics and the Los Alamos National Laboratory).

An even better result was obtained from experiments involving measurements of solar winds (a solar wind is basically plasma coming from the sun, which carries a magnetic field with itself).

It turns out that if the photon had a mass, this plasma would behave differently, namely, there would be current produced and the plasma would get accelerated.

Now, by observing the solar wind plasma and the maximum possible acceleration it could have (which is either very tiny or zero), it is possible to calculate an upper limit of 2×10^-54 kg for a photon’s mass (according to the same source as for the other value above).