Einstein Field Equations Fully Written Out: What Do They Look Like Expanded?
The Einstein field equations are a set of non-linear second order partial differential equations, which are often described as extremely complicated and in most cases, very hard to solve.
That’s because they really are extremely complicated, but it might not be obvious if you’re using the very compact tensor notation. In this notation, the Einstein field equations are as follows:
In reality, this one equation really includes 16 different equations, one for each combination of µ and ν, which can both be either 0,1,2 or 3 (in reality, there is actually only 10 independent equations due to some symmetry properties).
Moreover, these quantities seen in the usual form of the field equation are actually much more complicated.
Fundamentally, however, they all contain the metric tensor gµν so it is indeed possible to expand the above equation in terms of the metric only (and its derivatives).
This is what the fully expanded Einstein field equations look like when written out in terms of the metric:
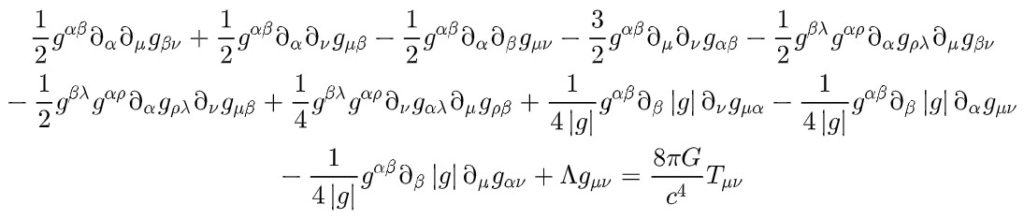
Even this does not really describe how complicated these equations actually are.
Here I’ve used the so-called Einstein summation convention, which means that every index you can see in a term that is repeated both in the upstairs and downstairs position, is actually a summation index.
If you want to explicitly write out the summations, this is what it would look like:
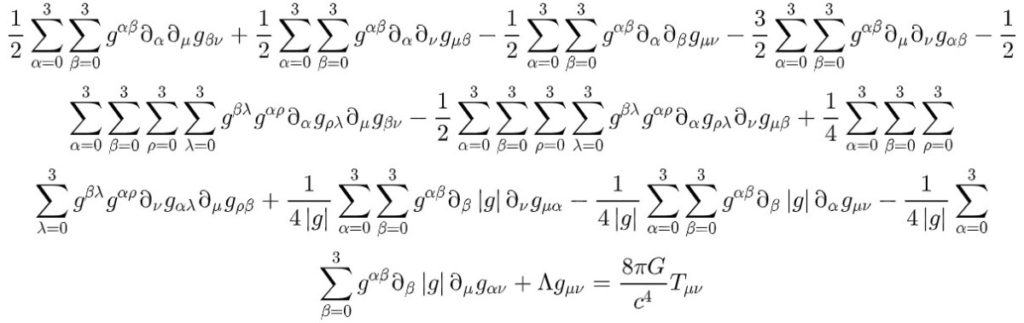
It’s kind of a mess, isn’t it? If you were to write out all of these sums (which would not even fit on this whole page probably), the result would be even messier.
To give you some idea, here is the first term completely written out:
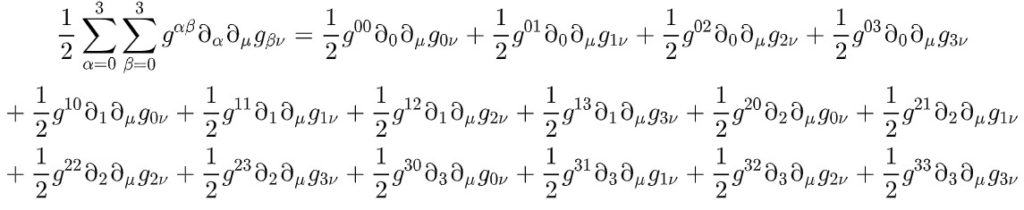
Yes, this really is only the first term. Good luck then writing out the summations for every single term in the field equations, let alone solving that equation for any component of the metric.
Of course, it’s obvious no one will actually use this kind of form of the Einstein field equations (please do yourself a favor and do not use this form for anything!).
The point of this was to just give you some idea of how complicated the Einstein field equations really are and how powerful the typical tensor notation actually is in terms of compactifying the equations.
If you wish to learn more about these field equations and general relativity, consider reading my introduction to general relativity.
In case you’re interested in seeing specifically where the Einstein field equations come from, check out this article, where we derive the field equations step by-step. You can also get the article as a PDF version for free here.