Momentum vs Kinetic Energy: Why They Are Not The Same

When I first started learning physics, momentum and kinetic energy seemed like they were almost the same thing to me. I didn’t understand why it was useful to have two very similar quantities as they both depend on mass and increase with velocity. So, are momentum and kinetic energy the same or not?

In short, momentum and kinetic energy are not the same as momentum is a vector (has a direction) and kinetic energy is a scalar (does not have a direction). Momentum also increases linearly with velocity while kinetic energy increases quadratically, so their values are not the same at higher velocities.

There are, of course, a lot of other factors that make these two quantities quite different and useful in different contexts.

The goal of this article is to give a comprehensive explanation of all of these (how they differ, but also how they’re similar), so you’ll be able to understand why both of these are useful in physics.

Here’s a table of the most important differences between kinetic energy and momentum:

Kinetic energy	Momentum
Is a scalar quantity	Is a vector quantity
Is always positive (>0)	Can be either positive or negative (>0 or <0)
Depends quadratically on velocity	Depends linearly on velocity
Depends on even powers of velocity (in special relativity)	Depends on odd powers of velocity (in special relativity)
Is conserved only in special cases	Is always conserved

In this article, we’ll go deeper into all of these ideas and also discuss the relationship between these two quantities. Later, we’ll also look at the differences from a more advanced physics point of view, such as how relativity and quantum mechanics play into this.

As a quick overview, here is a table showcasing kinetic energy, momentum and their relationship (an equation relating the two) in some of the more advanced areas of physics – we will talk about what all of them actually mean later:

Area of physics	Kinetic energy (T)	Momentum (p)	Relationship between kinetic energy and momentum
Newtonian mechanics	T=\frac{1}{2}m\vec{v}\cdot\vec{v}	\vec{p}=m\vec v	T=\frac{\vec{p}\cdot\vec{p}}{2m}
Advanced mechanics (Lagrangian & Hamiltonian)	T=\frac{1}{2}m\vec{v}\cdot\vec{v}	p_i=\frac{\partial L}{\partial v_i}	\frac{\partial T}{\partial v_i}=p_i+\frac{\partial V}{\partial v_i}
Special relativity	T=\left(\gamma-1\right)mc^2	\vec{p}=\gamma m\vec{v}	T=\sqrt{\vec{p}\cdot\vec{p}c^2+m^2c^4}-mc^2
Quantum mechanics	\hat{T}=-\frac{\hbar^2}{2m}\nabla^2	\hat{p}=-i\hbar\nabla	\hat{T}=\frac{\hat{p}^2}{2m}

I recommend you to keep reading as we’ll discuss all of these and what they mean later in the article.

Why Is Momentum a Vector While Kinetic Energy Is a Scalar?

Kinetic energy is considered a scalar as it describes the total energy associated with motion, meaning that kinetic energy does not have any particular direction in space. Meanwhile, momentum describes motion in a specific direction, meaning that it has a different value in each spacial direction.

To understand this, let’s think of the definitions for kinetic energy and momentum (in this article, kinetic energy is denoted by T for reasons having to do with Lagrangian mechanics, while momentum is denoted by p):

T=\frac{1}{2}mv^2=\frac{1}{2}m\vec{v}\cdot\vec{v}

Here, v² really means the dot product of the velocity vector with itself (magnitude of the velocity vector squared).

\vec p=m\vec v

From these, it’s easy to see that kinetic energy is a scalar since it involves the square of the velocity (dot product of the velocity vector with itself; a dot product is always a scalar!). Also, momentum is clearly a vector since it involves the velocity vector.

Since one is a vector and the other is a scalar, this means that kinetic energy and momentum will both be useful, but in quite different contexts:

• Kinetic energy is typically more useful in problems where the direction of motion doesn’t matter, while momentum is more useful when describing motion in different directions.
• Momentum is more useful if we want to determine which way an object is moving (such as when a force is applied and we want to know which way the object will begin moving).
• Kinetic energy, on the other hand, is usually easier to work with if we only wish to know the change in the position of an object (for example, when determining how the height of an object changes as it falls due to gravity).

Also, momentum being a vector quantity, this means that it has both a magnitude and a direction. Compare this to kinetic energy, which only has a magnitude. Kinetic energy is simply a single number (scalar), but momentum has a magnitude in each direction of space.

In other words, momentum can always be divided into its vector components (which represent how much momentum an object has in each direction). This is done by simply calculating the velocity components on whatever coordinate system you’re using.

Here’s a little comparison of both the momentum components and kinetic energy in different coordinate systems:

Coordinate system	Momentum components	Kinetic energy
Cartesian (x,y,z)	p_x=mv_x\\p_y=mv_y\\p_z=mv_z	T=\frac{1}{2}m\left(v_x^2+v_y^2+v_z^2\right)
Spherical (r,θ,φ): x=r\cos\varphi\sin\theta\\y=r\sin\varphi\sin\theta\\z=r\cos\theta	p_r=mv_r\\p_{\theta}=mrv_{\theta}\\p_{\varphi}=mr\sin\theta v_{\varphi}	T=\frac{1}{2}mv_r^2+\frac{1}{2}mr^2\left(v_{\theta}^2+\sin^2\theta v_{\varphi}^2\right)
Cylindrical (r,φ,z): x=r\cos\varphi\\y=r\sin\varphi\\z=z	p_r=mv_r\\p_{\varphi}=mrv_{\varphi}\\p_z=mv_z	T=\frac{1}{2}m\left(v_r^2+r^2v_{\varphi}^2+v_z^2\right)

Don’t worry if you’re not familiar with how some of these quantities are obtained. The point is that for momentum, three different values (its components) are required to specify it. On the other hand, only one value is needed to specify the kinetic energy (its magnitude).

Quadratic vs Linear Velocity Dependence

One of the most obvious differences between kinetic energy and momentum is that kinetic energy depends quadratically on velocity (it increases as v²), while momentum depends linearly on velocity (it increases as just v).

This means that kinetic energy actually increases way faster with velocity as momentum does. A nice way to visualize this is by graphing them both as shown below.

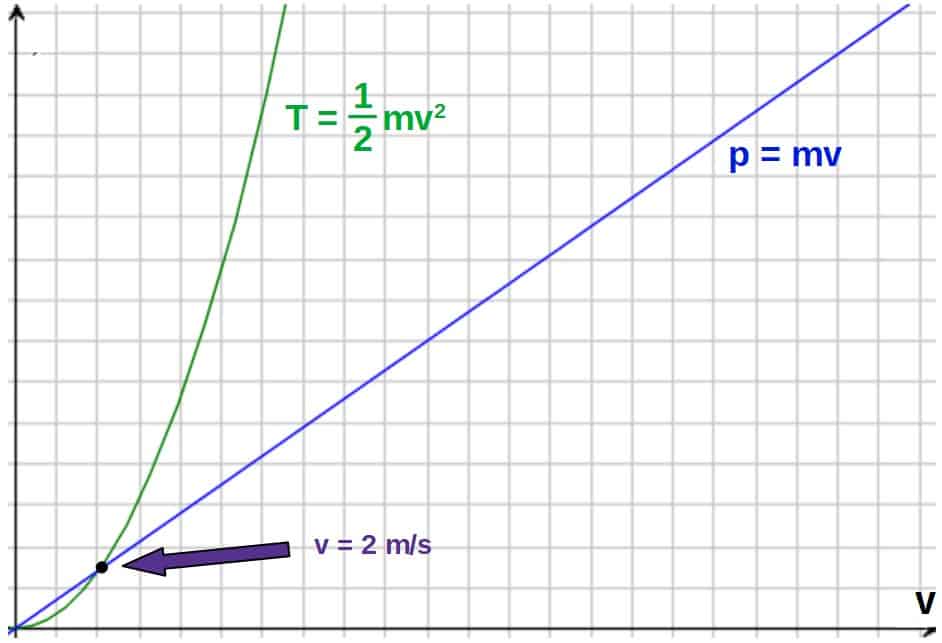
Intuitively, the formula for momentum makes perfect logical sense as it is just the product of mass and velocity (although this definition is not entirely correct, as we’ll see later).

Kinetic energy, however, is not as straightforward and it may seem odd at first that it has a v² -term. So, why exactly is kinetic energy proportional to velocity squared?

Kinetic energy being proportional to velocity squared is simply a mathematical consequence of the work-energy theorem, which results from force being integrated over distance. If special relativity is accounted for, it also predicts that kinetic energy should be proportional to velocity squared.

Below you’ll find a derivation of the kinetic energy formula. The derivation uses calculus and is a bit more advanced, but the point is that it makes no assumptions (except the work-energy theorem and Newton’s second law), which should help in understanding where exactly this v² -dependence of kinetic energy comes from.

Also, if you’re interested in why exactly this kinetic energy formula has a half in it, I actually have a whole article discussing this. There I explain how the half appears as a result of special relativity and also why it’s useful in the context of Lagrangian mechanics.

Derivation of Kinetic Energy Using Vector Calculus (click to see more)

Odd vs Even Powers of Velocity (According To Special Relativity)

There is also another, arguably more fundamental way to see why momentum has a linear velocity-dependence and kinetic energy has a quadratic one and this comes from special relativity.

I actually have a whole section later in the article discussing both momentum and kinetic energy in special relativity (and in general relativity!), but for the short summary, momentum and kinetic energy in special relativity are given by the following equations:

\vec{p}=\gamma m\vec{v}

This formula for the momentum is really just a “special case” of something called four-momentum, which you can read more about in my special relativity article.

T=\left(\gamma-1\right)mc^2

This γ-factor is called the Lorentz factor and it is defined as follows:

\gamma=\frac{1}{\sqrt{1-\frac{\vec{v}\cdot\vec{v}}{c^2}}}=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}

These formulas are actually more fundamental definitions than the typical ones you’re probably used to from ordinary mechanics.

The interesting thing is that this Lorentz factor can be expanded in something called a Taylor series (which has infinitely many terms of increasing exponents) as follows:

\gamma=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}=1+\frac{1}{2}\frac{v^2}{c^2}+\frac{3}{8}\frac{v^4}{c^4}+\frac{5}{16}\frac{v^6}{c^6}+...

If we now insert this to the formulas for the momentum and kinetic energy, we then get:

\vec{p}=m\vec{v}+\frac{1}{2}m\vec{v}\frac{v^2}{c^2}+\frac{3}{8}m\vec{v}\frac{v^4}{c^4}+... T=\left(1+\frac{1}{2}\frac{v^2}{c^2}+\frac{3}{8}\frac{v^4}{c^4}+\frac{5}{16}\frac{v^6}{c^6}+...-1\right)mc^2 \Rightarrow\ T=\frac{1}{2}mv^2+\frac{3}{8}m\frac{v^4}{c^2}+\frac{5}{16}m\frac{v^6}{c^4}+...

From this, we can see an interesting fact; momentum contains terms with v, v³, v⁵ and so on, while kinetic energy has terms with v², v⁴, v⁶ etc.

In other words, a more accurate statement of “momentum depends linearly on velocity and kinetic energy quadratically” would actually be that momentum depends on odd powers of velocity, while kinetic energy depends on even powers of velocity.

Now, the significance of this is that kinetic energy will always be positive, while momentum can be either positive or negative. This is because any even power of velocity has to be positive.

This is, of course, true in ordinary Newtonian mechanics (where T=1/2mv²), but it is also true in special relativity.

Also, if we’re dealing with sufficiently small velocities (below about 10% of the speed of light), it is enough to just pick the first terms of these sums (which gives the usual p=mv and T=1/2mv²).

Momentum Conservation vs Conservation of Kinetic Energy

An important distinction between momentum and kinetic energy is that, in certain situations, their conservation properties may be different.

Momentum is always a conserved quantity, while kinetic energy is not. Kinetic energy may be converted to other forms of energy, but total momentum in a system always remains the same. Examples of this are collisions in which momentum is conserved, but kinetic energy gets converted into heat and sound.

This really comes down to how we define these two quantities. Kinetic energy is only one form of energy (other forms include mass and potential energy) and the conservation of energy only applies to total energy.

Now, the total energy in any system will always be conserved (this is the law of energy conservation!), but there is no conservation law specifically for kinetic energy. Therefore, it can always get converted to other forms of energy.

In contrast, there is no such thing as momentum being converted to “other forms of momentum”. Therefore, momentum is always conserved in a given system (it will always be conserved if you actually take into account the whole universe).

This is, however, a little more technical than it may first appear. Momentum actually comes in two forms: linear momentum and angular momentum.

The first one, linear momentum, is the usual form of momentum given by the formula p=mv. Angular momentum, on the other hand, is the momentum associated with rotating or spinning motion.

The important thing is that these two forms of momenta cannot be converted into one another and they are also independently conserved. So, the bottom line is that momentum is always conserved, while kinetic energy may not be.

For a deeper look at momentum conservation compared to kinetic energy conservation, you can check out this article. The article also covers some examples of when kinetic energy is conserved and when it’s not, as well as the same for momentum.

Noether’s Theorem For Momentum and Kinetic Energy Conservation

Noether’s theorem is one of the most fundamental theorems having to do with conservation laws. Noether’s theorem can also help us understand how the conservation of momentum and kinetic energy differ and why.

Essentially, Noether’s theorem states that for every symmetry in the laws of physics of a system, there exists an associated conservation law. For example, if a system has a translational symmetry, it means that the total momentum will be conserved.

For understanding Noether’s theorem, I would recommend reading my complete guide on it here. It should give you everything you need if you want to learn more about Noether’s theorem.

You can also watch this short video explaining the basic idea of Noether’s Theorem:

The key point about Noether’s theorem is that it states that there exists a conservation law for momentum. Namely, momentum conservation is related to spacial translation and symmetries associated with them.

On the other hand, there is no conservation law for kinetic energy according to Noether’s theorem. There is certainly a conservation law for total energy, but not specifically to kinetic energy.

Energy conservation is also one of the topics we look at in my complete guide on Noether’s theorem. The article will show you where energy conservation fundamentally comes from in physics (hint; it has to do with something called time translation symmetry).

Now, in some cases, if the only form of energy an object has is kinetic energy (and probably mass as well), then the conservation of total energy will correspond to kinetic energy being conserved.

In other words, there are certain situations where kinetic energy is conserved, but it is not necessarily always conserved while momentum, on the other hand, is always conserved.

Differences Between Momentum and Kinetic Energy In Collisions

One of the most important differences between momentum and kinetic energy in terms of their applications can be seen in collisions. The distinction here comes from how the two quantities are conserved in collisions.

Now, a collision in physics is simply a process in which two (or more) objects interact in such a way that they exert forces on one another. Usually, a collision is defined as an event in which the objects exert forces on each other for a fairly short duration (think of a car crash, for example).

Collisions are typically classified as either elastic or inelastic based on how they conserve (or change) the kinetic energy of a system. Total momentum will always be conserved in all types of collisions as it is generally a conserved quantity.

In rare special cases, a collision can also be super-elastic (which I’ll explain soon).

Are momentum and kinetic energy conserved in all collisions?

Generally, momentum is conserved in all collisions. Kinetic energy, however, is not conserved in all collisions, only in special cases called elastic collisions. In the case of an inelastic collision, some kinetic energy is always converted to heat or sound, meaning that it is not conserved.

An elastic collision is defined as a “perfect collision” in which no kinetic energy is converted to heat or anything else. In this case, the kinetic energy is conserved also.

Inelastic collisions, on the other hand, are the opposite. They are defined as collisions in which kinetic energy DOES get converted to heat, sound or other forms of energy.

It’s worth noting that in the real world, all collisions are inelastic up to some extent (no collision is perfectly elastic in reality), but sometimes a collision can be approximated as elastic to very good accuracy. In any case, momentum will always be conserved in all types of collision, as required by the law of momentum conservation.

Now, some confusion may sometimes arise from the fact that kinetic energy may not be conserved even though there does exist a conservation law for energy.

The key here is that while total energy is always conserved, kinetic energy specifically may not be (as explained in the section about Noether’s theorem) and this applies to collisions as well.

So, while kinetic energy may not be conserved in a collision, if you were to theoretically measure and add up ALL the different forms of energy associated with a system (heat, sound etc.), the total energy would remain the same before and after a collision (it would be conserved).

Under what conditions is kinetic energy conserved in a collision?

Kinetic energy is conserved under the condition that the collision is elastic. An elastic collision is a collision in which no kinetic energy is converted to heat, sound or any other forms of energy, meaning that the kinetic energy will remain the same (it is conserved).

Elastic collisions, however, are quite rare in the real world (no real collision is ever perfectly elastic).

This means that kinetic energy is typically not very useful in calculations regarding most collisions, because we cannot usually calculate the “lost” energy very accurately (by “lost”, I mean the kinetic energy that was converted to other forms of energy).

Momentum, however, is conserved in all collisions and it just transfers between the colliding objects. Therefore, the momenta of each object involved in the collision can often be calculated much more accurately by applying the conservation law for momentum (total momentum at the start = total momentum at the end).

Can a collision conserve kinetic energy without conserving momentum?

In general, it is not possible for a collision to conserve kinetic energy without conserving momentum as the law of momentum conservation prohibits this. This can, however, occur the other way around, meaning that a collision can conserve momentum without conserving kinetic energy.

The collisions in which momentum is conserved but kinetic energy is not are again called inelastic collisions. However, there does not exist a collision type in which momentum would not be conserved.

Can kinetic energy increase after collision?

In some cases, kinetic energy can increase after a collision and this is called a super-elastic collision. In this type of collision, some potential or chemical energy of the objects involved is converted into kinetic energy, meaning that the total kinetic energy is actually higher after the collision.

This may seem unintuitive at first, but all that’s really happening is that a collision causes a different type of interaction to happen (such as a chemical reaction, like an explosion).

Let’s say that there are two balls colliding with each other. If the other ball has a nitroglycerin core (a very realistic example, I know!), then a collision between these balls would likely cause the nitroglycerin to detonate.

In this case, the explosion (a chemical reaction) would release a huge amount of chemical energy that would be converted into the kinetic energy of the other ball (the explosion would cause the other ball flying off with a much greater velocity than before the collision). This would be an example of a super-elastic collision.

Super-elastic collisions are even thought to occur naturally in some cases. Examples of this are collisions between plasmoids caused by the Sun, according to a 2012 study published in the Nature Physics -journal.

Plasmoids are essentially clumps of plasma that have a specific shape due to a magnetic field. In the study mentioned above, the researchers essentially looked at coronal mass ejections caused by the Sun (which are plasmoids).

They then concluded that these plasmoids behaved in a way that was very similar if not identical to a super-elastic collision (the kinetic energies of the plasmoids actually increased as they collided, just like how super-elastic collisions would work).

Relationship Between Kinetic Energy and Momentum

The relationship between kinetic energy and momentum is given by the equation T=p²/2m, where T is kinetic energy, p is momentum and m is mass. This relationship comes directly from the definitions of momentum (p=mv) and kinetic energy (T=½mv²).

The derivation of this formula is extremely simple. Since momentum is p = mv, we can rearrange that to v = ^p⁄_m and substitute it in the kinetic energy formula for v like this:

T=\frac{1}{2}m\vec{v}\cdot\vec{v}\ \ \ \left(\vec{v}=\frac{\vec{p}}{m}\right)\\\Rightarrow\ \ T=\frac{1}{2}m\left(\frac{\vec{p}}{m}\cdot\frac{\vec{p}}{m}\right)=\frac{1}{2}m\frac{1}{m^2}\left(\vec{p}\cdot\vec{p}\right)\\T=\frac{\vec{p}\cdot\vec{p}}{2m}=\frac{p^2}{2m}

From just that one formula, we could easily calculate either the momentum or the kinetic energy of an object if we know the other.

Down below, we’ll explore some of the consequences of this equation.

Also later in the article, we’ll look at how this relationship holds in other areas of physics, such as special relativity and quantum mechanics (hint; it’s actually very fascinating!).

Does more momentum mean more kinetic energy?

Generally, the more momentum an object has, the more kinetic energy it will also have. This is because both momentum and kinetic energy depend on velocity, so if one increases, the other one will as well. It is possible, however, for momentum to be negative while kinetic energy is always positive.

This is quite easy to see from the relationship between kinetic energy and momentum:

T=\frac{p^2}{2m}

Here, it’s quite clear that if p increases, so will T and vice versa. This is, however, only true for the magnitude of the momentum.

If momentum were to be negative and increase in the negative direction (i.e. decrease), then a decrease in momentum would result in an increase of kinetic energy.

Now, momentum being negative is somewhat arbitrary since it only depends on which way we choose the positive velocity -direction to be.

Let’s say the positive direction is to the right and there is an object moving to the left with mass m and velocity v. In this case, the velocity and momentum are negative.

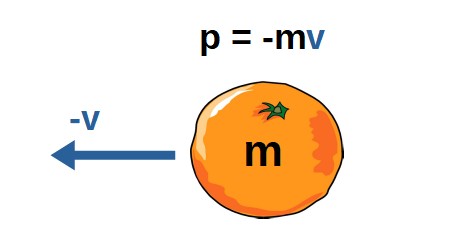
The kinetic energy for this object will be:

T=\frac{p^2}{2m}=\frac{\left(-mv\right)^2}{2m}=\frac{mv^2}{2}

This is obviously a positive number. Generally, kinetic energy is always positive because it contains a v² -term and the square of a (real) number is always positive.

Is momentum proportional to kinetic energy?

In short, momentum is proportional to the square root of kinetic energy since momentum is directly proportional to velocity, while kinetic energy is proportional to velocity squared. This means that if kinetic energy becomes four times as big, the momentum will only double.

This can also be seen from the relationship between momentum and kinetic energy if we solve for p:

T=\frac{p^2}{2m}\ \ \Rightarrow\ \ p=\sqrt{2mT}

Here I’ve left out the negative square root.

From this, it’s easy to see that momentum is proportional to the square root of kinetic energy, while kinetic energy is proportional to the square of momentum:

T\propto p^2\ \ \ \ \ \ \ p\propto\sqrt{T}

Can an object have kinetic energy but no momentum?

A single object cannot have any kinetic energy if it has no momentum. This is because an object with no momentum implies it has no velocity either, which also means no kinetic energy. However, a system of multiple objects can have kinetic energy but no momentum in total.

Once again, we can see from the relation T=p²/2m that if an object has no momentum (p=0) then it also cannot have kinetic energy (T=0).

In the case of multiple objects, however, it’s possible to have no momentum (zero total momentum), but non-zero kinetic energy. This can be seen from the example given below.

Does zero momentum mean zero kinetic energy?

For a single object, zero momentum always means zero kinetic energy as well. However, for systems of multiple objects, it is possible to have zero total momentum but non-zero kinetic energy in the case that the momenta of each object is exactly equal but in opposite directions.

In the case of a single object, this is easy to see directly from the formula T=p²/2m. If the momentum of this object is zero, the kinetic energy will be as well.

However, the case with multiple objects is easiest to understand through an example. Let’s say we have two objects of the same mass moving in opposite directions with the same velocity (equal magnitude but different sign). This means that they have equal but opposite momentum:

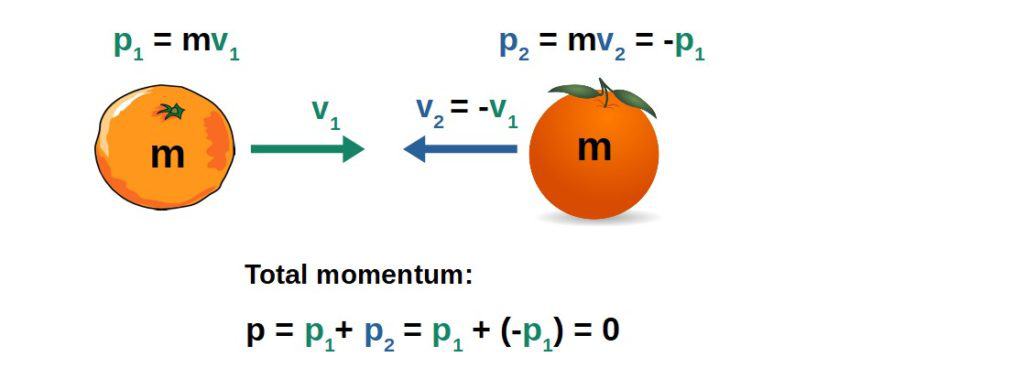
In this case, the kinetic energy will be the sum of the kinetic energies of each object:

T=T_1+T_2=\frac{p_1^2}{2m}+\frac{p_2^2}{2m}

Since p₁=-p₂ and the masses are the same, this becomes:

T=\frac{p_1^2}{2m}+\frac{\left(-p_1\right)^2}{2m}=\frac{p_1^2}{2m}+\frac{p_1^2}{2m}=\frac{p_1^2}{m}

We can also insert p₁=mv₁ so that this becomes:

T=\frac{m^2v_1^2}{m}=mv_1^2

This is clearly non-zero and we therefore have an example of a case where the total momentum is zero, but kinetic energy is not.

Is Momentum The Derivative of Kinetic Energy?

When I first got started learning calculus, the first thing I noticed was that the equations for momentum and kinetic energy looked very similar.

Namely, momentum (p=mv) looked like the derivative of kinetic energy (T=1/2mv²), but it wasn’t clear to me if that was correct or not since one should be a vector and the other a scalar. So, is momentum actually the derivative of kinetic energy and why?

In short, momentum is the derivative of kinetic energy with respect to velocity as it describes the directional change in kinetic energy as the velocity changes. The derivative of kinetic energy with respect to velocity produces a vector quantity (momentum), similarly to a gradient of a scalar function.

The key thing here is the fact that momentum is a vector while kinetic energy is a scalar. Because of this, it’s not quite as simple as just taking an ordinary derivative.

Naively, when I first noticed this, my first thought was to just take the derivative of kinetic energy with respect to velocity like this:

p=\frac{dT}{dv}=\frac{d}{dv}\left(\frac{1}{2}mv^2\right)=\frac{1}{2}m\cdot2v=mv

This certainly does work, however, it is not quite correct. The problem is that this only deals with magnitudes of velocity and momentum, but in reality, these are both vector quantities.

The correct thing to do is a vector derivative (derivative of kinetic energy with respect to the velocity vector). Technically, the correct notation should also use a partial derivative, similarly as to how a gradient also uses partial derivatives.

If you’re confused about whether it’s possible to take a derivative with respect to a vector, the answer is that it certainly is possible.

In physics, derivatives with respect to vectors (vector derivatives) are very common and in fact, also the commonly used gradient is a form of a vector derivative.

Now, what does taking a derivative with respect to a vector actually mean? It simply means that we take the derivative with respect to each component individually. This then produces another vector quantity:

\vec{p}=\frac{\partial T}{\partial\vec{v}}=\frac{\partial T}{\partial v_x}\overline{\text{i}}+\frac{\partial T}{\partial v_y}\overline{\text{j}}+\frac{\partial T}{\partial v_z}\overline{\text{k}}

In the section below, you’ll find some details about how exactly this works.

Momentum as the Derivative of Kinetic Energy Using Vector Calculus (click to see more)

The interesting thing about momentum as the derivative of kinetic energy is what it physically represents.

Kinetic energy, at a high level, is the energy associated with motion. Momentum can then be thought of as a measure of how much this kinetic energy changes in a particular direction.

This also helps to explain why momentum is a vector and kinetic energy a scalar and how exactly they differ.

Think of it this way: if the velocity of an object changes, say in the x-direction, then the derivative of kinetic energy with respect to the x-velocity gives you the momentum in the x-direction.

Therefore, physically, a positive x-component of the momentum represents an increase in kinetic energy due to an increase in velocity in the x-direction and vice versa (a negative x-momentum represents a decrease in kinetic energy).

Also, the importance of momentum being the derivative of kinetic energy may not be clear quite yet, but it is extremely important in Lagrangian mechanics (which I’ll explain later). In Lagrangian mechanics, this basically works as a definition for momentum.

Kinetic Energy As The Integral of Momentum

If momentum is the derivative of kinetic energy, does this mean that kinetic energy is then the integral of momentum?

In short, kinetic energy is indeed the integral of momentum with respect to velocity. More accurately, the line integral of momentum with respect to the velocity vector at each point along a path gives the total change in kinetic energy. Physically, this represents the work done along the path.

The change in kinetic energy is mathematically defined as:

\Delta T=\int_{v_1}^{v_2}\vec{p}\cdot d\vec{v}

Technically, this is actually a line integral, which simply means an integral along a specific path.

Now, the physical meaning of this is that by adding up (integrating) all the momenta at each point along a path described by a certain velocity at each point, we can calculate the total change in kinetic energy between the end points of the path (see the picture below).

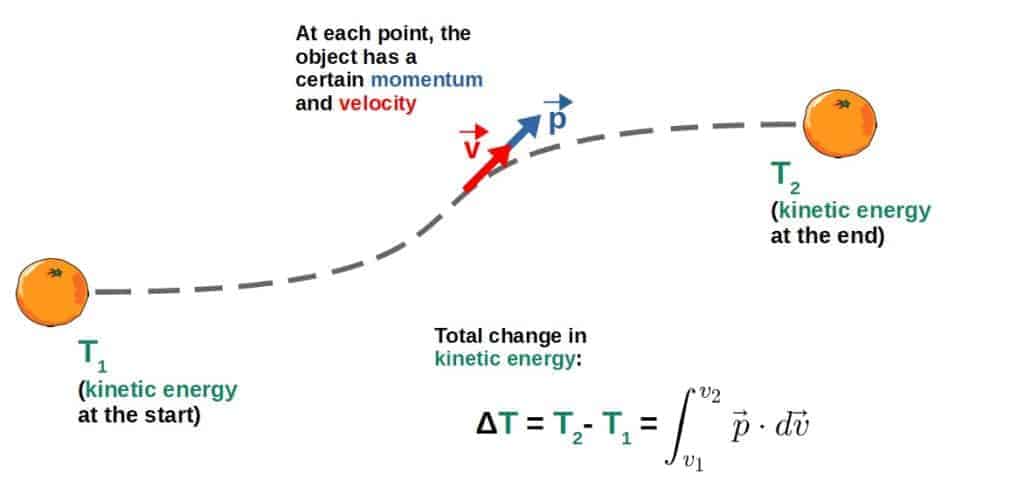
Also, the mathematical proof you can use to verify that this works is extremely easy; just plug in p=mv and calculate the integral. You can see this quite easily by simply writing out the dot product and splitting out the integrals component by component:

\Delta T=\int_{ }^{ }\vec{p}\cdot d\vec{v}=\int_{ }^{ }p_xdv_x+\int_{ }^{ }p_ydv_y+\int_{ }^{ }p_zdv_z

Derivative of Kinetic Energy With Respect To Momentum (Hamilton’s Equation!)

An interesting extra fact is that velocity can actually be expressed as the derivative of kinetic energy with respect to momentum. All we do for this is use the following formula for kinetic energy in terms of momentum:

T=\frac{\vec{p}\cdot\vec{p}}{2m}

Then, we take the derivative of this with respect to momentum:

\frac{dT}{d\vec{p}}=\frac{d}{d\vec{p}}\left(\frac{\vec{p}\cdot\vec{p}}{2m}\right)=\frac{1}{2m}\left(2\vec{p}\right)=\frac{\vec{p}}{m}=\vec v

Here, I’ve used the fact that velocity v=p/m.

This is just a fun little insight and not very useful, but essentially this idea is an oversimplification of one of Hamilton’s equations of motion, which on the other hand, has a lot of significance in advanced classical mechanics.

Hamilton’s equation is defined as follows:

\frac{\partial H}{\partial p_i}=\frac{dq_i}{dt}

In this equation, H represents the Hamiltonian (which is basically the total energy of a system and in many cases, it’s some form of p²/2m), p_i is the i:th component of something called generalized momentum (for example, p_x would be the x-momentum) and dq_i/dt is the generalized velocity (time derivative of “position”, which is represented by generalized coordinates in advanced mechanics).

If you’re interested, a simple introduction to Hamiltonian mechanics can be found here, although I would recommend reading this introduction to Lagrangian mechanics first.

Momentum vs Kinetic Energy In Lagrangian Mechanics

Typically in mechanics, things are described by forces and Newton’s laws. However, in more advanced classical mechanics, the same concepts (motion, dynamics etc.) are most often described by energies. This is what Lagrangian mechanics is all about.

In Lagrangian mechanics, everything is described by energies and it is always done by defining a Lagrangian for any given system.

Generally, for any system, the Lagrangian is the difference between the kinetic and potential energies of each object in the system:

L=T-V

Now, if you’re interested to learn more about this, I’d recommend reading my introductory article on Lagrangian mechanics.

Anyway, the point here is that kinetic energy in Lagrangian mechanics is the exact same as it is in “ordinary” mechanics.

Momentum, on the other hand, has a different definition. Momentum in Lagrangian mechanics is defined as the derivative of the Lagrangian with respect to velocity:

p_i=\frac{\partial L}{\partial v_i}

The i-index here represents the components of the momentum and velocity. For example, setting i=x would give the x-component of momentum.

This is actually not quite the correct definition yet, but from this, you can clearly see the similarity to what I explained earlier about momentum as the derivative of kinetic energy.

In Lagrangian mechanics, it is typical to use generalized coordinates (which are labeled by q’s). By using these, the definition for momentum is a little different, but the basic idea is the same. You can read more about this as well in my introductory article (link above).

Anyway, in most cases, the above definition is simply just momentum equals the derivative of kinetic energy, however, not always.

Namely, if the potential (V in the Lagrangian) happens to be dependent on velocity, then the momentum won’t be as simple as p=mv anymore.

Example: Charged Particle In An Electromagnetic Field (click to see more)

The bottom line here is essentially this:

• In Lagrangian mechanics, kinetic energy is still the usual 1/2mv².
• Momentum, however, is defined differently in Lagrangian mechanics.
• In many cases, momentum will be the usual p=mv also in Lagrangian mechanics, but not necessarily always.

If you are interested in learning more about Lagrangian mechanics (and you should – it’s used pretty much everywhere in modern physics!), I’d highly recommend checking out the book Lagrangian Mechanics For The Non-Physicist (link to the book’s page). The book explains things in a way with pretty basic high school level math and physics should be able to understand.

Momentum vs Kinetic Energy In Special Relativity

In special relativity, both momentum and kinetic energy are defined a little differently and the special relativistic formulas are valid at high velocities (close to the speed of light), while the usual classical formulas are not.

This γ-term is called the Lorentz factor and it is a function of velocity defined as follows:

\gamma=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}

Here, c is the speed of light and thus, this Lorentz factor only becomes significantly greater than 1 if the object’s velocity is high enough.

The key point in special relativity is that all the equations are slight corrections to classical mechanics which only come to play at high velocities.

In the slow velocity limit (also called classical limit), these formulas both actually reduce to the usual p=mv and T=1/2mv², which I explain in my introductory article on special relativity.

Anyway, the goal of this section is to look at the relationship between momentum and kinetic energy in special relativity. It is possible to derive the following expression for kinetic energy in terms of momentum:

T=\sqrt{p^2c^2+m^2c^4}-mc^2

This equation is actually the relativistic equivalent of the p²/2m -relation between kinetic energy and momentum.

We can easily see that this is the case if we expand this square root term using the binomial theorem (if you don’t know how to do this, don’t worry, the point of this is to just show how this equation relates to the classical one).

When doing this, we essentially get an infinite series of terms of increasing order:

T=\frac{p^2}{2m}-\frac{p^4}{8m^3c^2}+\frac{p^6}{16m^5c^4}+...

From this, it may be easier to see the similarity to the classical equation:

In special relativity, there is also an analogous relation of momentum as the derivative of kinetic energy. It is, however, slightly different as it contains an extra factor of γ²:

\gamma^2\vec{p}=\frac{\partial T}{\partial\vec{v}}

Based on this, we can also write kinetic energy as the integral of momentum as follows (more accurately, the change in kinetic energy):

\Delta T=\int_{v_1}^{v_2}\gamma^2\vec p\cdot d\vec v

Both of these equations are quite easy to verify if you simply know how to take derivatives and integrals. Next we’ll take a look at how this changes once we move to general relativity.

How Are Momentum and Kinetic Energy Different In General Relativity?

General relativity is a theory of gravity that incorporates the ideas of special relativity (spacetime, four-vectors and whatever else). If you wish to learn more about it, I’d recommend reading this introductory article on general relativity.

In general relativity, it is actually not possible to define a useful notion of kinetic energy. In some special cases, it may be possible, but generally not.

Now, let’s try to see why this is.

One of the simplest examples of general relativity is an object in the gravitational field of some mass M (a planet, star, black hole or whatever mass that’s spherically symmetric).

In this case, it’s possible to define a total energy for the object in terms of its momentum p:

E=\sqrt{\left(1-\frac{2GM}{c^2r}\right)m^2c^4+p^2c^2}

Here, M is the mass of the planet or whatever mass causing the gravitational field, m is the object’s mass itself, c is the speed of light, G is the gravitational constant and r is the distance (radius) between the object and the central mass M.

Here we can again use the binomial theorem and by doing that, we get a series of terms:

E=mc^2+\frac{p^2}{2m}-\frac{GMm}{r}+\frac{G^2M^2m}{2c^2r^2}+\frac{p^2}{2m}\frac{GM}{c^2r}\\+\frac{3p^2}{4m}\frac{G^2M^2}{c^4r^2}-\frac{p^4}{8m^3c^2}-\frac{3p^4}{8m^3}\frac{GM}{c^4r}+...

Maybe you can begin to see the problem here. We cannot define a notion of kinetic energy simply because there is no way to distinguish what the kinetic energy and what the potential energy here is.

At first glance, you could think of the terms with p as being the kinetic energy part, the terms with M as the potential energy part and the mc²-term simply the rest energy.

The problem, however, is that these “kinetic energy” and “potential energy” terms are intertwined in very complicated ways and we cannot separate them. This is actually very often the case in general relativity, which means that there isn’t a useful definition of kinetic energy in general relativity.

However, we can take the classical limit of this (ignore all terms with c in the denominator, since the speed of light is huge compared to any classical speeds). Doing that, we obtain for the total energy:

E\approx mc^2+\frac{p^2}{2m}-\frac{GMm}{r}

This is the usual total energy for an object in a gravitational field. The first term is the rest energy (E=mc²), the second term is the kinetic energy and the last term is the potential energy.

Anyway, the bottom line here is that while there is definitely a concept of momentum in general relativity (it’s actually called four-momentum, but that’s another story), there does not exist a general definition of kinetic energy.

Momentum vs Kinetic Energy In Quantum Mechanics

In quantum mechanics, the relation between kinetic energy and momentum is defined as:

\hat{T}=\frac{\hat p^2}{2m}

This is essentially the same as in classical mechanics, but the difference is that kinetic energy and momentum are operators in quantum mechanics, not actual physical quantities by themselves. These are represented by putting a “hat” over them.

But what are these operators used for? Essentially, in quantum mechanics there is something called the wave function, which describes any quantum system. These operators can then act on the wave function to obtain a physical quantity.

In the case of kinetic energy, the kinetic energy operator can act on a wave function ψ to obtain the physical quantity T (this is called the Eigenvalue of the kinetic energy operator, but essentially this is just a value for the kinetic energy, which you have to solve for):

\hat{T}\psi=T\psi

Or written in terms of the momentum:

\hat{T}\psi=\frac{\hat{p}^2}{2m}\psi=\frac{1}{2m}\hat{p}\left(\hat{p}\psi\right)

Also, the definitions of these operators can be expressed in terms of gradients as follows:

\hat{p}=-i\hbar\nabla \hat{T}=-\frac{\hbar^2}{2m}\nabla^2

Anyway, the point here is that in quantum mechanics, both momentum and kinetic energy are operators, which can act on a wave function to obtain the actual physical values of these. This means that neither momentum or kinetic energy are real physical quantities unless a wave function is specified.