Lagrangian vs Newtonian Mechanics: The Key Differences
When analyzing mechanical systems, Newtonian mechanics is often the most common approach, however, it is not the only one. Lagrangian mechanics is another useful approach, but what actually are the differences between Lagrangian and Newtonian mechanics?
In short, the main differences between Lagrangian and Newtonian mechanics are the use of energies and generalized coordinates in Lagrangian mechanics instead of forces and constraints in Newtonian mechanics. Lagrangian mechanics is also more extensible to other physical theories than Newtonian mechanics.
Down below is also a table comparing the key differences between these two formulations.
| Lagrangian mechanics | Newtonian mechanics |
|---|---|
| Motion is described by energies | Motion is described by forces |
| Based on the principle of least action | Based on Newton’s laws of motion |
| Generalized coordinates are used instead of constraint forces | Involves constraint forces |
| Conservation laws can be derived easily (Noether’s theorem) | Does not have a systematic method for deriving conservation laws |
| Does not use vectors (energy being a scalar) | Uses vectors |
| Not ideal for non-conservative forces (such as friction) | Can handle non-conservative forces quite well |
| Used widely in all areas of physics | Mainly applicable to classical physics and in describing everyday phenomena |
Next we’ll go ahead and look at each of these in more detail and what they actually mean through some practical examples.
Also, all of the things about Lagrangian mechanics that we’ll talk about are explained in this introductory article.
The information given in that article is not absolutely necessary to understand this one, but I’d recommend reading it if you’re not familiar with the Lagrangian formulation.
Table of Contents
The Underlying Principles Behind Lagrangian and Newtonian Mechanics
Probably the biggest and also most obvious difference between the two formulations is the underlying principles from which the equations of motion are derived.
Newtonian mechanics is primarily based on Newton’s three laws of motion (although the first law is technically already included in the second, but whatever):
- If no forces are present, an object will remain at rest or moving at constant velocity.
- The net force on an object equals the rate of change of its momentum:
- For every force applied on an object, there exists an equal but opposite force.
For the purpose of comparing these with Lagrangian mechanics, we’ll only focus on the second law, from which you commonly derive equations of motion.
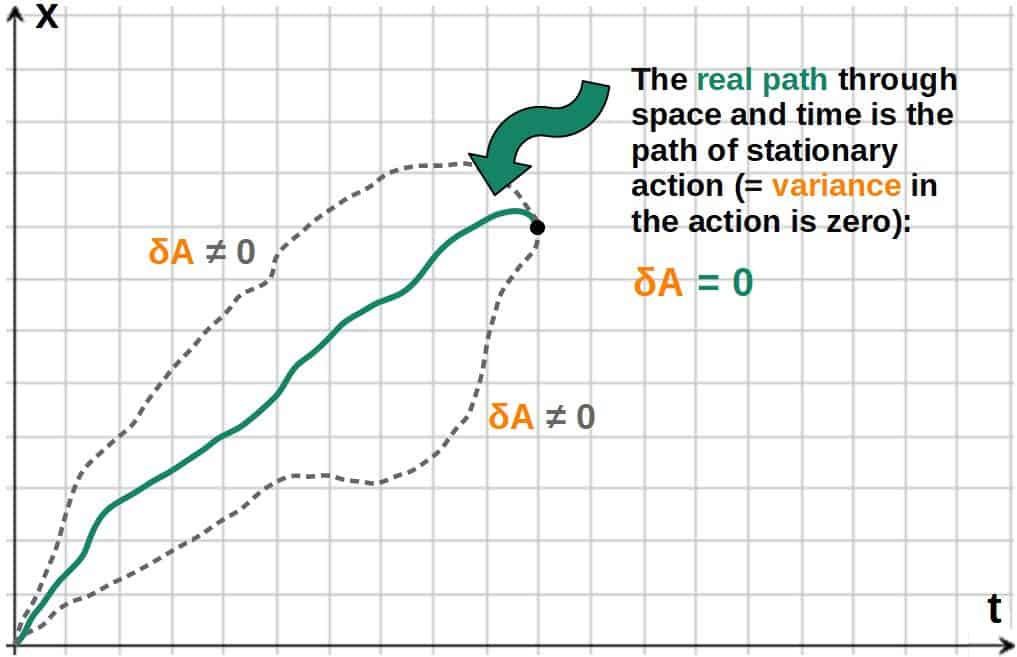
Lagrangian mechanics, on the other hand, is based on the principle of least action (principle of stationary action, to be more precise).
In simple terms, every possible path an object can take through space and time has a quantity called action associated with it (which is simply a number associated with that particular path).
The real path an object or a system takes is then the path in which this action is minimized or more accurately, stationary (hence the name principle of stationary action).
Compared to Newtonian mechanics, the underlying principles behind Lagrangian mechanics are much more fundamental and profound than those of Newtonian mechanics.
Newtonian mechanics isn’t really based on some fundamental principle, it rather comes from experimental and observational facts, at least historically. Therefore, Newtonian mechanics is really only valid for ordinary everyday phenomena.
The principle of least action, on the other hand, is more of a postulate of physics that is true for much more than just classical mechanics.
It is, in fact, one of the most fundamental principles in all of physics and it works in relativity, quantum theories, electrodynamics, you name it (this is explained more later).
In fact, Newton’s second law, F=ma, can actually be derived from the principle of least action (which I show in this article). This might indicate that perhaps it is actually just a special case of the Lagrangian formulation.
So, the short story is that Lagrangian mechanics certainly takes the cake for a more axiomatic theory than Newtonian mechanics. This, however, doesn’t state anything about which one is more useful practically and that is what we’ll look at next.
Problem Solving and Finding Equations of Motion
Both the Lagrangian formulation as well as the Newtonian formulation have their own characteristics, which this article plans to explore.
In this section, I’ll explain how the two formulations of mechanics differ in terms of finding equations of motion and solving problems in general.
I’ll go through the basic problem-solving steps for each formulation and then show an example of how you actually use these steps in practice.
Steps For Solving a Problem in Lagrangian Mechanics
Earlier, I talked quite a bit about the principle of least action, but what exactly is it?
Mathematically stated, the action is defined as an integral over time of a function called the Lagrangian (i.e. basically adding up all of the Lagrangians over the trajectory):
A=\int_{ }^{ }\mathscr{L}\ dtUsually a script L is referring to Lagrangian density, while a normal L refers to the Lagrangian but in this article, I’m loosely switching between the two (just note that it will still refer to the Lagrangian!)
In classical mechanics and for the purpose of comparing it to Newton’s laws, the Lagrangian is defined as the difference between kinetic energy (T) and potential energy (U):
\mathscr{L}=T-UNow, minimizing this action quantity is mathematically equivalent to plugging the Lagrangian into what is known as the Euler-Lagrange equation:
\frac{d}{dt}\frac{\partial\mathscr{L}}{\partial\dot{q}_i}=\frac{\partial\mathscr{L}}{\partial q_i}The q’s here represent generalized coordinates, which are a useful property of Lagrangian mechanics (these are explained more later in the article).
So, the Euler-Lagrange equation is essentially the condition for a trajectory in which the action is stationary. In other words, the equations of motion in Lagrangian mechanics are obtained from the Euler-Lagrange equation.
The Euler-Lagrange equation is an important mathematical result coming from calculus of variations. If you want to know more about that, I discuss calculus of variations in detail in this article.
The process for finding equations of motion in Lagrangian mechanics goes more or less like this:
- Find a set of convenient coordinates (= generalized coordinates, expressed by q’s) for the specific problem. It is usually easier to express these generalized coordinates first in terms of ordinary Cartesian coordinates (x, y, z).
- Define the Lagrangian through the generalized coordinates. The Lagrangian will generally be the sum of the kinetic and potential energies of every object of the system:
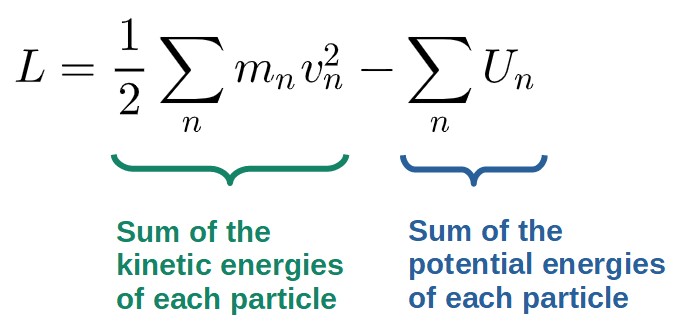
- Plug the Lagrangian into the Euler-Lagrange equations. You’ll have one Euler-Lagrange equation for each generalized coordinate (The q with a dot above means the time derivative of q, i.e. velocity):
- Simplify and solve the differential equations. At this point, you should have a set of second order differential equations (how many equations you have will depend on how many generalized coordinates you have).
Steps For Solving a Problem in Newtonian Mechanics
The problem-solving process for Newtonian mechanics essentially relies on Newton’s second law as well as dealing with vectors (forces being vectors, of course).
The steps for finding equations of motion in Newtonian mechanics follow more or less the following pattern:
- Identify all of the forces involved in the problem for each object.
- Draw a diagram or a picture of the different objects and force vectors (optional). This helps in identifying all of the different forces involved.
- Apply Newton’s second law for each object. Often it is much easier to turn vector equations into scalar form by breaking down the forces into components and writing an equation for each spacial direction separately. Doing this, you’ll get an equation for each direction, usually in the form:
The i here stands for spacial directions (for example, setting i=x would give the forces and acceleration in the x-direction).
- Simplify and solve the differential equations. At this point, you should have one second order differential equation for each spacial direction.

Energies (Lagrangian Mechanics) vs Forces (Newtonian Mechanics)
It is pretty straightforward to say that Newtonian mechanics relies very heavily on forces, which are the cornerstone of Newton’s laws.
Lagrangian mechanics, on the other hand, is based on the concept of a Lagrangian for a system, which is a function involving energies, namely the kinetic and potential energies.
Now, this distinction between forces and energies may not seem that important, but it is actually one of the main differences that differentiates Lagrangian mechanics from Newtonian mechanics.
This becomes much more prevalent when we try to extend these formulations of mechanics to other areas of physics (this is explained later in the article).
Scalars vs Vectors: Which Are More Useful?
A key difference between forces and energies is that one of them is a vector quantity while the other is a scalar.
Forces are defined as being vector quantities, which means that they generally have both a magnitude and a direction. This is why in Newtonian mechanics, it is common to deal with vectors and vector equations.
Energy, on the other hand, is a scalar quantity, which means that it only has a magnitude. Lagrangian mechanics, therefore, is built on the idea of using energies instead of forces to describe motion.
Typically, Lagrangian mechanics has a clear advantage in using energies since we don’t have to deal with directions, vectors and all that stuff.
It also makes a lot of sense intuitively why energy is a useful concept in Lagrangian mechanics, since it is so intimately connected with motion. In fact, energy by itself is enough to completely determine how an object moves through space and time.
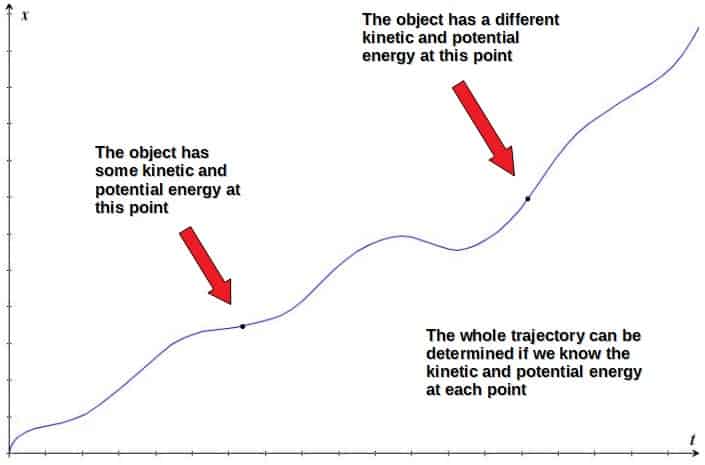
Also in the Lagrangian approach, there is simply one Lagrangian for the whole system, while in Newtonian mechanics, you have multiple different component forms of Newton’s second law.
For example, if you’ve been given the total velocity of some object, it is usually simpler to use the Lagrangian approach since you just have to write down the kinetic energy in terms of the total velocity:

In the Newtonian formulation, you would generally have to break down the velocity into different components (such as the x and y -components) and find the different components of acceleration and forces from those:
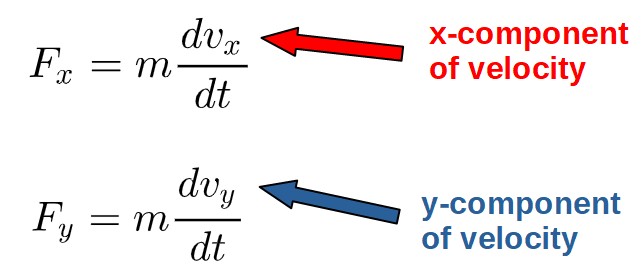
Also, the idea of forces doesn’t carry over well to more modern and advanced fields of physics, but the notion of energy certainly does. This is one of the reasons why Lagrangian mechanics is much more important outside of classical mechanics.
Constraint Forces vs Generalized Coordinates
One of the key differences between Lagrangian and Newtonian mechanics, particularly in the context of how they can be used in problem solving, is the way the two formulations handle constraints.
A constraint is simply a kind of rule that constrains a system or object to only be able behave or move in a certain way. For example, a constraint could allow an object to only move along a particular surface.
In Newtonian mechanics, constraints to systems are introduced in the form of constraint forces. For example, the normal force acting on an object sitting at rest on the ground is a constraint force.
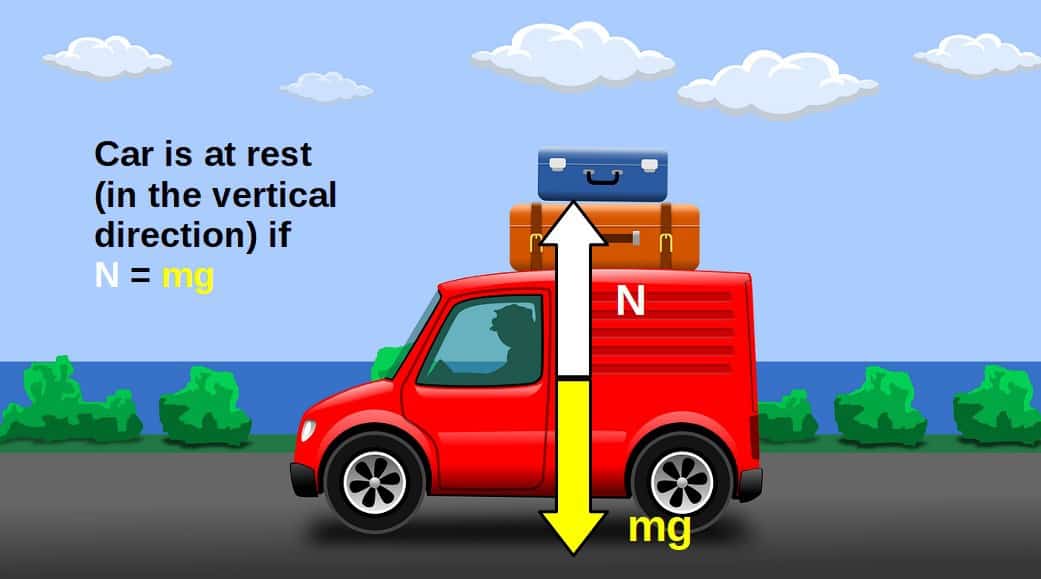
Why? Because the fact that the object is sitting at rest constrains the dynamics of the system by allowing the gravitational force downwards to only take on certain values. Namely, values where the normal force is equal to the gravitational force (otherwise the object wouldn’t be at rest).
The problem with constraint forces in Newtonian mechanics is that they get increasingly harder to deal with when there are a lot of constraints imposed on the system.
This is because there is no clear cut way to calculate the constraint forces since they typically depend on the dynamics of the specific problem.
For example, there is no explicit general formula to calculate the normal force on an object. The normal force is simply another unknown to the problem, which might depend on the mass of the object, the surface material, gravitational acceleration etc.
The nice thing about Lagrangian mechanics is that by choosing a suitable set of generalized coordinates, such that they implicitly encode the constraints themselves, we can essentially bypass the whole process of adding these constraint forces.
This then allows us to find the right equations of motion that are completely consistent with all the constraints, but without actually adding in any unnecessary constraint forces.
I discuss all about how to do this and the key points about generalized coordinates in this article. In there, I also show you a bunch of step-by-step examples of how generalized coordinates work in practice.
Now, sometimes we may actually want to know the constraint forces themselves. Maybe we would like to know when certain constraints break down and for this, knowing the constraint forces is necessary.
We can also do this in Lagrangian mechanics fairly straightforwardly by using something called Lagrange multipliers. I explain all about these and also show examples in this article, which I’d highly recommend checking out.
Just to give you a quick idea of how these Lagrange multipliers work, essentially, they are really closely related to the constraint forces that we’re used to in Newtonian mechanics.
Now, I think it’s worth discussing the use of generalized coordinates more and how these replace the notion of constraint forces. After all, generalized coordinates are basically the thing that makes Lagrangian mechanics so powerful.
I’ve included a little example of this below, but for a lot more and a deeper discussion of generalized coordinates, I recommend reading the full article on generalized coordinates linked above.
How Do Generalized Coordinates Replace Constraint Forces?
In Lagrangian mechanics there is actually another approach to replace the constraint forces in Newtonian mechanics. I’ve been talking quite a bit about generalized coordinates so far, which is what we’ll look at closer here.
In short, generalized coordinates in Lagrangian mechanics are specific choices of coordinates that will often implicitly encode the constraints in a system. Thus, generalized coordinates replace constraint forces from Newtonian mechanics and can be used to easily calculate constrained equations of motion.
So, in principle, If we choose our generalized coordinates wisely, we could obtain equations of motion (which implicitly already contain the constraints of the problem) without even using the Lagrange multiplier method.
The simple pendulum essentially consists of a mass at the end of a rigid rod that swings in a plane under the influence of gravity. The length of the rod is L, the mass of the “pendulum bob” is m and the gravitational acceleration downwards is g (a constant).
We can place the pendulum in an x,y -coordinate system such that the rod is attached to the origin. I’ll also denote the angle relative to the vertical (y-axis) as θ.
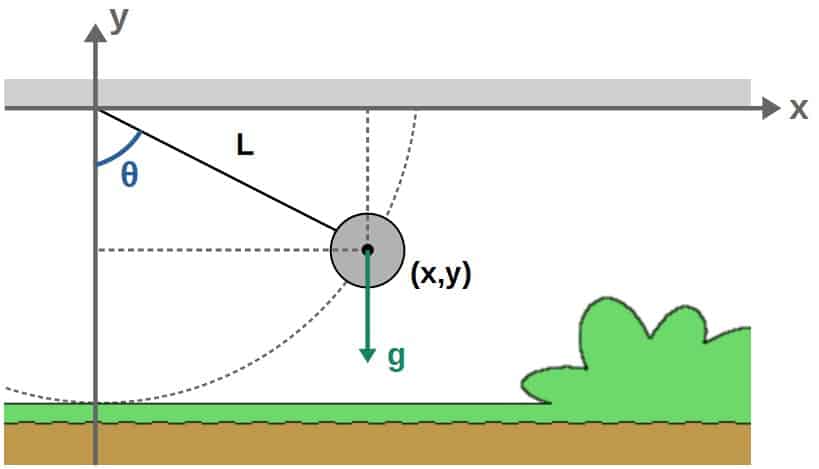
What we want to do is to find the pendulum bob’s position at each point in time and then construct the Lagrangian. To do this, we could use the x,y -coordinates here, but these may not be the best choice.
Let me explain why. First of all, we have once constraint, which is that the length of the rod or the distance from the origin has to be a constant L.
Therefore, we only have 2*1-1=1 (we’re in two dimensions with one object and one constraint) degrees of freedom here and thus, we only need one generalized coordinate.
The natural choice due to rotational symmetry here is going to be the angle θ (which changes with time as the pendulum swings back and forth).
This is indeed a valid choice of a generalized coordinates as it is consistent with our constraint; this θ-coordinate can only change perpendicularly to our constraint (distance from the origin), so it cannot violate this constraint.
I discuss all about how generalized coordinates can be best chosen in this article.
So, we will take the angle θ as the generalized coordinate of this pendulum. Now, the easiest way to continue here is to write down the x,y -coordinates in terms of θ. We can get these by some simple trigonometry:
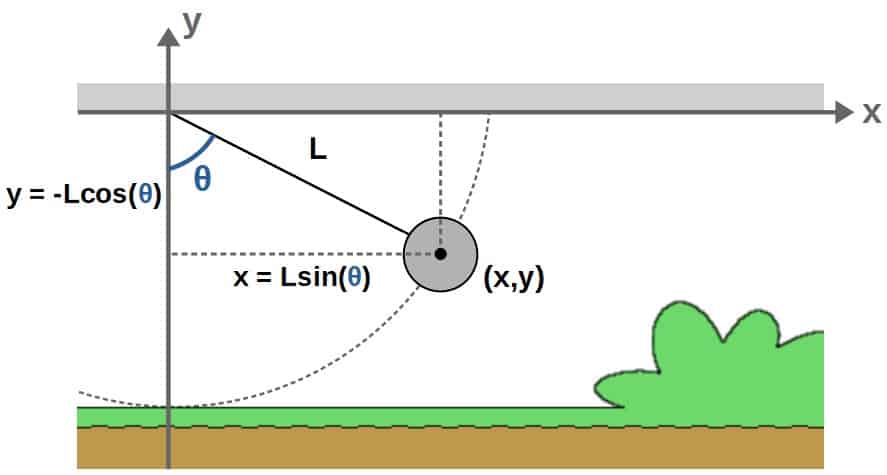
The next step is to construct the kinetic energy. For this, we need the velocities and again, the easiest way to get these is just by differentiating the x,y -coordinates (using the chain rule since θ here is a function of time):
\dot{x}=L\dot{\theta}\cos\theta \dot{y}=L\dot{\theta}\sin\thetaThe kinetic energy is then simply:
T=\frac{1}{2}m\left(\dot{x}^2+\dot{y}^2\right)=\frac{1}{2}m\left(L^2\dot{\theta}^2\cos^2\theta+L^2\dot{\theta}^2\sin^2\theta\right)=\frac{1}{2}mL^2\dot{\theta}^2
Here I’ve used cos2θ+sin2θ=1.
Notice how simple obtaining the kinetic energy is if you first write down the Cartesian coordinates in terms of your generalized coordinates. All we need after that is to take the time derivatives and them sum the squares of the Cartesian velocities.
The potential energy is simply going to be V=mgh. If we choose the zero-level of the potential at y=0, then the height h is just the y-coordinate:
V=mgh=-mgL\cos\thetaThe Lagrangian is then:
L=T-V=\frac{1}{2}mL^2\dot{\theta}^2+mgL\cos\thetaWe now have the Lagrangian of this simple pendulum system in terms of the generalized coordinate θ! The Euler-Lagrange equation is then (we only have one for the generalized coordinate θ!):
\frac{d}{dt}\frac{\partial L}{\partial\dot{\theta}}=\frac{\partial L}{\partial\theta}And from this, we get the standard pendulum differential equation:
mL^2\ddot \theta=-mgL\sin\theta \ddot{\theta}=-\frac{g}{L}\sin\thetaNotice from the above example that by introducing generalized coordinates, we didn’t have to specify any constraint forces! We still ended up with an equation of motion that contains the constraints, without having to do almost anything.
This goes to show the power of the Lagrangian mechanics approach over the Newtonian mechanics approach.
Now, the only downside of this method is that since we completely skipped over having to deal with the constraints, we also didn’t obtain any information about the constraint forces, such as tension.
For that, we would have to use the Lagrange multiplier method (which I discuss in detail here).
However, if we only care about the motion and not the constraints themselves, then generalized coordinates provide a very powerful method to obtain equations of motion.
The bottom line with these examples, however, is that Lagrangian mechanics can deal much better with constraints than Newtonian mechanics, especially in the case of some more complicated systems.
Conservation Laws
One of the clear advantages that Lagrangian mechanics has over Newtonian mechanics is a systematic way to derive conservation laws.
In general, Newtonian mechanics doesn’t really have a simple and systematic method to find conservation laws, they are more so approached on a case-by-case basis.
Lagrangian mechanics, on the other hand, has a nice theorem associated with it, from which it is fairly simple to systematically derive conservation laws and find conserved quantities. This theorem is called Noether’s theorem.
Essentially, Noether’s theorem states that for every symmetry in the laws of physics of a system, there exists an associated conservation law. A symmetry means that the value of the Lagrangian does not change even if there is a change in a particular generalized coordinate.
Before going further, I would highly recommend checking out my complete guide on Noether’s theorem. It will teach you everything you need to know about it in a beginner-friendly way as well as show lots of examples.
Now, if the above statements seem a little abstract, down below is an interesting example showing how all of this works.
Consider the Earth revolving around the Sun according to this picture:
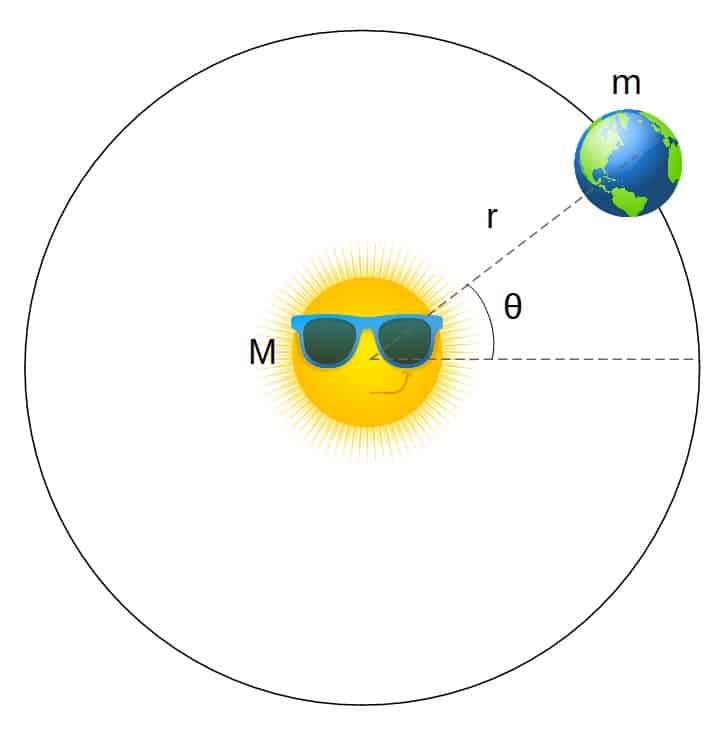
From the parameters given in the picture, we can derive the Lagrangian to be (for the full derivation, you can see here):
L=\frac{1}{2}m\left(\dot{r}^2+r^2\dot{\theta}^2\right)+\frac{GMm}{r}The dots above these quantities mean their time derivatives.
Now consider rotating the system by some angle Δθ in the following way:
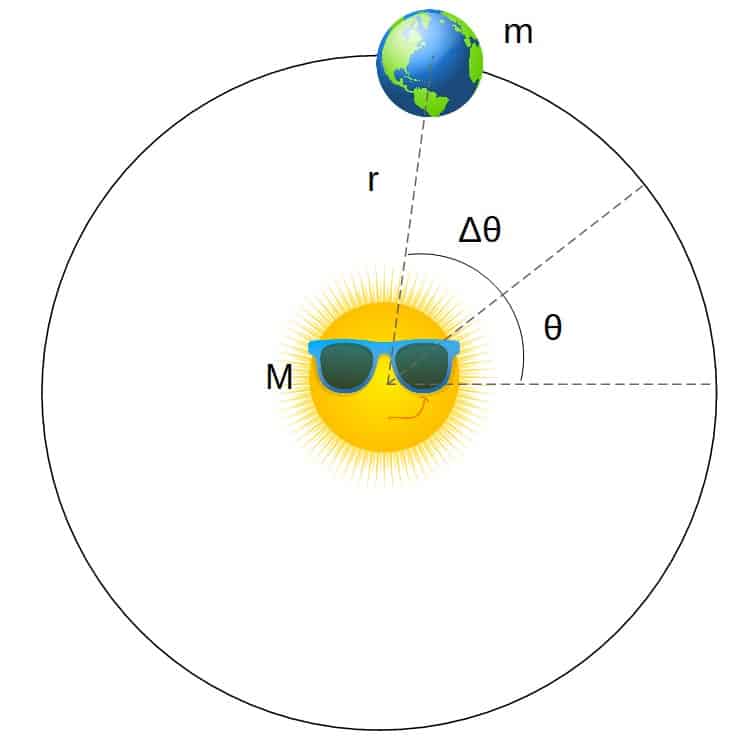
The angle specifying Earth’s position now becomes:
\theta\ \Rightarrow\ \theta+\Delta\thetaSo, what happens to the Lagrangian in this case? Well, let’s see. The Lagrangian only involves θ in this time derivative, so the Lagrangian now becomes:
L=\frac{1}{2}m\left(\dot{r}^2+r^2\left(\dot{\theta}+\frac{d\Delta\theta}{dt}\right)^2\right)+\frac{GMm}{r}By definition though, Δθ is just a constant (it is simply a number, which we rotated the system with) and the derivative of a constant is zero, so we just end up with:
L=\frac{1}{2}m\left(\dot{r}^2+r^2\dot{\theta}^2\right)+\frac{GMm}{r}This is exactly what we started with! So, the Lagrangian remained completely unchanged under this rotation, which means that the system has a rotational symmetry (symmetry associated with the generalized coordinate θ).
By Noether’s theorem, there must then be a conserved quantity, which we can find by simply applying the Euler-Lagrange equations on this Lagrangian (for the coordinate θ):
\frac{d}{dt}\frac{\partial L}{\partial\dot{\theta}}=\frac{\partial L}{\partial\theta}Here, the Lagrangian does not depend explicitly on θ, so the right-hand side becomes 0 and we get:
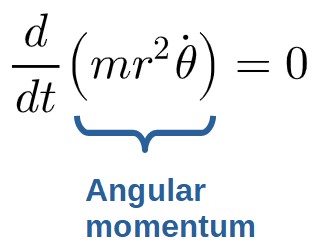
Now, by definition, the time derivative of something being zero means that it is conserved (i.e. a constant). So, we’ve just derived the conservation of angular momentum.
Now, the example above only showed how angular momentum is conserved.
More generally, Noether’s theorem states that if there is a symmetry associated with a change in any generalized coordinate of the form q ⇒ q + Δq (i.e. the Lagrangian remains unchanged), then there must exist a conserved quantity Q, meaning:
\frac{d}{dt}Q=0The big three conservation laws coming from Noether’s theorem (although there are more as well) are:
- Position-translation symmetry (x ⇒ x + Δx) → momentum conservation
- Time-translation symmetry (t ⇒ t + Δt) → energy conservation
- Rotational symmetry (θ ⇒ θ + Δθ) → angular momentum conservation
Now, it is certainly possible to prove these conservation laws by using Newton’s laws (only in limited cases though!), but there isn’t really a structured plan to do this.
Next, I want to show a little example of how conservation laws are found in both of the formulations and compare their effectiveness.
Practical Example: Energy Conservation (in Newtonian Mechanics vs in Lagrangian Mechanics)
In this example we’re going to see how conservation laws follow from Newton’s equations as well as from the Lagrangian formulation.
Now, I actually discuss energy conservation in a lot more detail (as well as derive it from first principles) in my complete guide on Noether’s theorem. So feel free to check that out as well.
In particular, we’ll compare the effectiveness of both methods and whether they can be generalized to any system.
Energy conservation in Newtonian mechanics is done by using Newton’s second law and making a few assumptions about the forms of the momentum and kinetic energy.
First, let’s see how conservation of energy can be proven with Newton’s second law, F=dp/dt.
If we assume the force to be a conservative force (i.e. one that conserves energy), it can be expressed as the negative derivative of a potential:
-\frac{dU}{dx}=\frac{dp}{dt}\Now let’s consider another way of writing dp/dt. Based on the chain rule, we know that:
\frac{dp^2}{dt}=2p\frac{dp}{dt}Divide both sides by 2p and we have:
\frac{dp}{dt}=\frac{1}{2p}\frac{dp^2}{dt}But, what’s p2? If we assume the usual form for the kinetic energy, then we can express the kinetic energy T as:
T=\frac{p^2}{2m} p^2=2mTInserting this result into the expression for dp/dt, we get:
\frac{dp}{dt}=\frac{1}{2p}\frac{d}{dt}\left(2mT\right)=\frac{m}{p}\frac{dT}{dt}Then Newton’s second law takes the form:
-\frac{dU}{dx}=\frac{m}{p}\frac{dT}{dt} -\frac{dU}{dx}\frac{p}{m}=\frac{dT}{dt}If we assume that p=mv (the usual expression for momentum), then p/m is simply the velocity (dx/dt):
-\frac{dU}{dx}\frac{dx}{dt}=\frac{dT}{dt}Here, the dx’s cancel and moving everything to one side, we get:
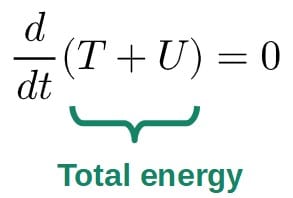
This of course is nothing but energy conservation! So, we can indeed prove the conservation of energy by using Newton’s second law, but here we’ve naively assumed that the kinetic energy and momentum have the usual forms:
T=\frac{1}{2}m\left(\frac{dx}{dt}\right)^2 p=m\frac{dx}{dt}In general, they won’t always (in more complex situations) have these forms and in those cases, there may not be a simple way to prove the energy conservation by using Newton’s laws.
The problem with the above example is that it only works nicely in very specific cases. If the system was more complicated (say, a double pendulum), the conservation of energy would be extremely difficult to prove in any reasonable sense.
In Lagrangian mechanics, on the other hand, energy conservation can be derived from Noether’s theorem, which states that the energy of a system is conserved if the system has a time-translation symmetry (i.e. the Lagrangian is invariant under time translations).
Another way to state it is to use one of Hamilton’s equations of motion, which relates the rate of change in energy to the Lagrangian in the following way:
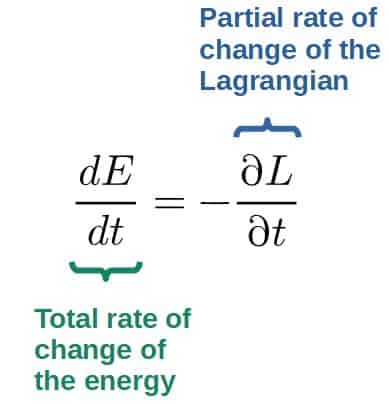
From this we can see that if the Lagrangian is not explicitly dependent on time, the right hand side is zero.
So, the equation above gives us a systematic rule for energy conservation:
The energy of a system is conserved if the Lagrangian does not explicitly depend on time.
This is actually just another way to state Noether’s theorem; if the Lagrangian does not depend on time, the system must be symmetric under time-translations, because a time-translation does not change the value of the Lagrangian.
Let’s in fact see just how powerful this rule can be. Consider a double pendulum consisting of two masses (m and M) connected by rods (with lengths r and R) swinging in a gravitational field:
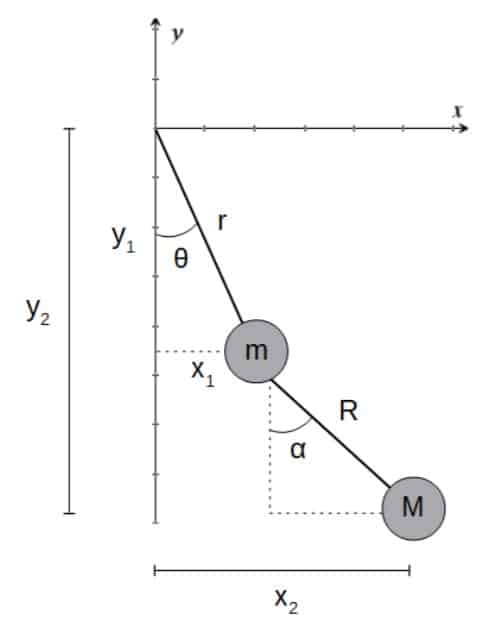
The Lagrangian for this double pendulum can be derived to be:
L=\frac{1}{2}\left(m+M\right)r^2\dot{\theta}^2+\frac{1}{2}MR^2\dot{\alpha}^2+MR\dot{\alpha}r\dot{\theta}\cos\left(\theta-\alpha\right)+mgr\cos\theta+Mg\left(r\cos\theta+R\cos\alpha\right)For the full derivation of this Lagrangian, see my Hamiltonian mechanics example problem set, which you’ll find in this article.
From this, it’s clear that the Lagrangian cannot be time dependent explicitly (sure, there is time dependence on the velocities and angles, but those do not matter in terms of energy conservation) since there is no explicit time terms.
Therefore, the Lagrangian is also invariant under time-translations and we have energy conservation based on Noether’s theorem.
This can also be proven easily by just plugging the Lagrangian into the Hamilton’s equation (from earlier).
Since the Lagrangian is independent of time, the partial derivative with respect to t is zero and we get energy conservation of the form:
\frac{dE}{dt}=-\frac{\partial L}{\partial t}=0The example above clearly demonstrates how easily energy conservation just comes as a simple consequence of certain symmetries in the Lagrangian.
So, in order to find out whether the energy is conserved all we have to know is the Lagrangian of the system. This is an extremely powerful and useful method for analyzing physical systems, which Newtonian mechanics simply doesn’t provide.
The bottom line is that Lagrangian mechanics is much more useful compared to Newtonian mechanics in deriving conservation laws and finding conserved quantities in different physical systems, which can be done by applying Noether’s theorem.
How Can The Lagrangian and Newtonian Formulations Take Into Account Non-Conservative Forces?
So far, I’ve been talking quite a bit about the positive sides of Lagrangian mechanics. While it’s true that the Lagrangian formulation is much more powerful compared to Newtonian mechanics in many ways, it does have its downsides too.
In particular, the whole concept of Lagrangian mechanics very much relies on the use of conservative forces. These are forces which conserve the energy of a system (Lagrangian mechanics being built on the notion of energies).
Conservative forces are in general, forces that can be derived from a potential, namely in the following way (I have a whole article comparing conservative and non-conservative forces, which you’ll find here):
\vec{F}=-\vec{\nabla}UThis is why the Lagrangian approach works so well in deriving the same results as Newtonian mechanics without ever even having to introduce the idea of forces. It’s because the system is usually assumed to conserve the total energy.
This is, of course, not always the case. Generally speaking, Lagrangian mechanics does not do well with non-conservative systems, although friction can still be dealt with using the Lagrangian formulation, which I show in this article.
In Newtonian mechanics, it is possible to deal with non-conservative forces more easily, but even then it is kind of a hassle. There are certainly models for non-conservative forces, which are more conveniently introduced to the Newtonian formalism.
Therefore, typically when dealing with these kinds of non-conservative systems, it is easier to use Newtonian mechanics.
Lagrangian mechanics, however, can account for frictional and non-conservative forces too, but the problem is that they can’t come from the principle of least action, which is the basis for Lagrangian mechanics.
So, the way they’re introduced into Lagrangian mechanics is a little arbitrary and it is done by using something called a dissipation function, but it does certainly work.
The dissipation function (how friction is incorporated into Lagrangian Mechanics):
D=\frac{1}{n+1}\sum_j^{ }c_jv_j^{n+1}
I explain everything about the dissipation function in this article as well as show a bunch of examples of how friction is incorporated into Lagrangian mechanics, so read it if you want to know more.
The bottom line though, is that friction is almost always easier to deal with in Newtonian mechanics, which is one of its clear advantages.

Applications To Other Areas of Physics
The purpose of this last section is to give you an idea and a bit of motivation as to how both the Newtonian as well as the Lagrangian formulation are used in other fields of physics.
To put it simply, Newtonian mechanics is more applicable to many engineering fields and practical uses, while Lagrangian mechanics is more useful in describing the principles of nature as well as applying it to other physical theories, such as general relativity and quantum field theory.
Now, let me explain this in a bit more detail.
Newtonian mechanics is mainly considered useful in classical mechanics and dynamics. It also has wide uses in the context of many engineering fields, such as in civil engineering or mechanical engineering.
Sure, Newton’s laws also have uses in many areas such as thermodynamics and electromagnetism, but when you get to the more modern theories of physics, the Newtonian formulation becomes somewhat outdated and only an approximation of more fundamental concepts and theories.
What I mean by this is that, in a fundamental sense, reality is governed by the laws of quantum mechanics, quantum field theories and relativity.
Newton’s laws and forces in general don’t really play an important role in these theories anymore, which are more so built on the notions of energy, momentum, symmetries and conservation laws, all of which play a more prevalent role in Lagrangian mechanics.
Lagrangian mechanics, as compared to Newtonian mechanics, is a formulation built on the principle of least action.
This makes the Lagrangian formulation extremely useful in almost all areas of physics, because it turns out that, actually, almost all physical theories are based on an action principle.
The more technical reason behind this is that Lagrangian mechanics is based on the field of mathematics known as calculus of variations, however, so are most other areas of physics. For this reason, many of the concepts you see in Lagrangian mechanics are easily applicable to other areas of physics as well.
If you’re interested to know more about this, I recommend checking out my complete guide to calculus of variations. In there, I also discuss many of the applications of this area of math to modern physics.
For example, the Einstein field equations of general relativity can be derived by using the principle of stationary action and a specific action integral. I explain this briefly in my introduction to general relativity.
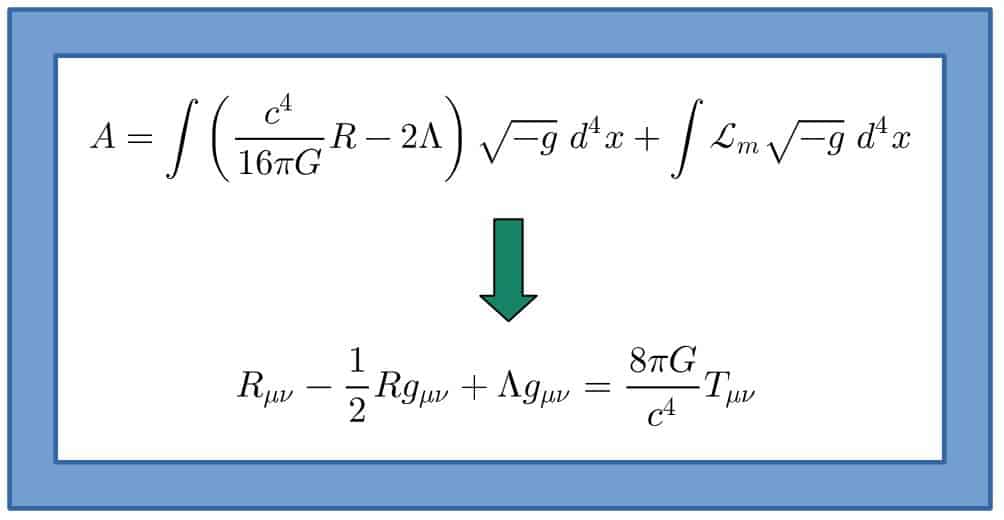
Lagrangians are also widely used in quantum field theory, which is arguably one of the most accurate theories of reality so far. Well, in QFT, you actually use something called the path integral formulation, which reduces to the principle of least action in the classical limit.
Even the famous equation, E=mc2, actually follows from a specific Lagrangian (which actually has a little bit of a different form than just T-U): (if you’re interested, I show this in my special relativity article):
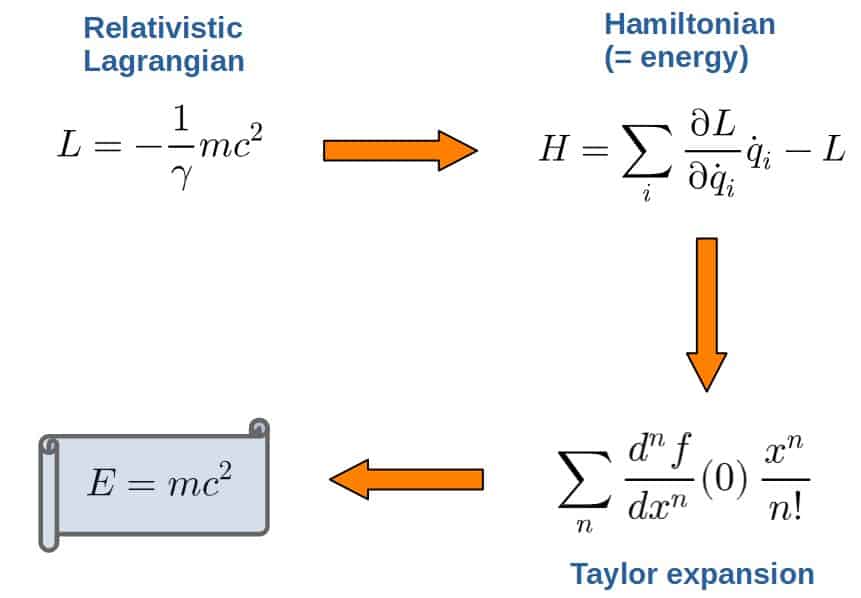
On the other hand, Lagrangian mechanics isn’t as widely used in many engineering fields as Newtonian mechanics is (although Lagrangians are actually used quite a bit in robotics).
This is most likely because of the fact that the Lagrangian formulation is more so concerned with being an axiomatic kind of theory that is more principle-focused, while the Newtonian formulation is more focused on practicality instead of things like conservation laws or symmetries of nature.
Now, if you’re interested in learning all of this much more deeply, you might enjoy my full, self-contained books on Lagrangian mechanics (found here) and on field theory, which uses Lagrangian mechanics very heavily (you’ll find that here).