If Photons Have No Mass, How Can They Have Momentum?

As a consequence of Einstein’s theory of special relativity, it is a known fact that photons, which are travelling at the speed of light, do not have any mass. A photon, however, does still have momentum, but how exactly?

In short, even though photons have no mass, they still have momentum proportional to their energy, given by the formula p=E/c. Because photons have no mass, all of the momentum of a photon actually comes from its energy and frequency as described by the Planck-Einstein relation E=hf.

Now, it is not necessarily satisfying enough to just state the answer, so we’re going to see exactly why a photon has momentum and also derive the equations for the momentum of a photon and see how it follows from the theory of special relativity.

Also, if you’re wondering why exactly a photon has no mass in the first place, I’ve got an entire article on that.

Table of Contents

How Do We Know That Photons Are Massless?

First of all, how can we even know that photons are actually massless?

In short, the special theory of relativity predicts that photons are massless simply because they travel at the speed of light. This is also backed up by the theory of quantum electrodynamics, which predicts photons to be massless as a result of gauge symmetries and the Higgs mechanism.

These are all explained in my article Why Do Photons Have No Mass?, in which I also discuss the large amount of experimental evidence that suggests photons to be massless (as well as the theory behind it).

An interesting issue related to this also comes up with the fact that massless photons still appear to be affected by gravity (such as by getting deflected near a star). I explain how this is possible in detail in this article.

Does a Photon Even Have Momentum (And Why)?

Now, to answer this question, we need to know what a photon actually fundamentally is.

You may already be aware of the fact that light consists of electromagnetic waves.

This wave nature of light, however, is unable to explain some phenomena, such as the photoelectric effect, where a light beam can actually scatter off electrons from a piece of metal.

It was Einstein who won the Nobel prize for first proposing that actually, light consists of little finitely sized packets of energy, i.e. elementary particles.

These energy packets are then able to hit electrons and transfer their energy into kinetic energy for the electron. These packs of energy are called photons.

Now, from Einstein’s special relativity, we know that mass is just another form of energy, but in the case of a photon, since it is always moving at the speed of light, it can’t have any mass (as a consequence of Einstein’s equations).

But, of course the photon still has to have energy, otherwise it wouldn’t produce the photoelectric effect. The natural conclusion is then that all of the energy of a photon is in the form of motion.

This also leads to the fact that if a photon is moving and has energy, it must also have momentum.

In the case of the photoelectric effect, the fact that the electron gains momentum when it is hit by a photon must mean that the momentum is transferred from somewhere (from the photon).

Formula For The Momentum of a Photon (Complete Derivation)

Now, based on classical Newtonian mechanics and the formula p=mv, a photon would not have any momentum as it has no mass.

So, Newtonian mechanics must be incorrect in this case. We’ll need something more fundamental, the theory of special relativity.

The goal is to find a definition for momentum expressed in terms of energy that is not dependent on mass.

This is actually not too difficult and we can do it just by a few basic principles of relativity and some simple algebra.

The first thing we’ll need are the concepts of a spacetime interval and a proper time interval. These are explained in much more detail in my article on special relativity, which is aimed for beginners in the topic.

A spacetime interval is simply a path through both space and time, which is the same for all observers (i.e. Lorentz invariant).

The spacetime interval (denoted by dS) connects both space and time in the following way (analogous to the Pythagorean theorem):

Okay, then we need the definition for a proper time interval. Proper time is defined as the time measured from an observer’s own frame of reference (rest frame).

A proper time interval (dτ) is always invariant, while time measured from any outside observer’s frame may not be.

A proper time interval is connected to the spacetime interval by a factor of the speed of light squared:

\left(dS\right)^2=c^2\left(d\tau\right)^2

If you’re confused by these definitions, don’t worry, because these are only needed to derive the formulas we’re looking for. Just know that these are some of the most central concepts in special relativity.

Anyway, from these quantities, it is possible to derive a formula for momentum that works for photons as well. This is known as Einstein’s energy-momentum relation:

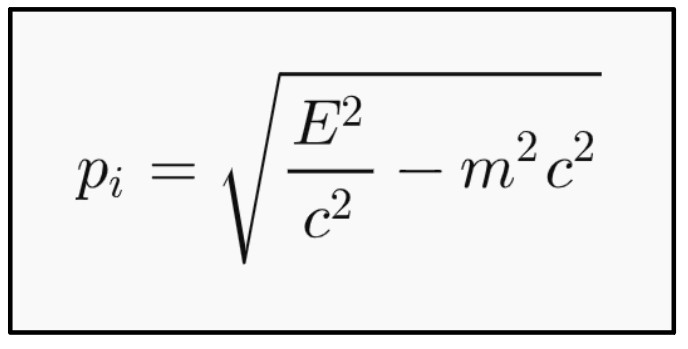
This image has an empty alt attribute; its file name is image-10.jpg

Derivation of Einstein's Energy-Momentum Relation (click to see more)

Okay, the first thing we can do is to manipulate the equation (just divide both sides by (dτ)²):

\left(dS\right)^2=c^2\left(d\tau\right)^2

\frac{\left(dS\right)^2}{\left(d\tau\right)^2}=c^2

Inserting the definition for a spacetime interval, we get:

c^2\frac{\left(dt\right)^2}{\left(d\tau\right)^2}-\frac{\left(dx\right)^2}{\left(d\tau\right)^2}-\frac{\left(dy\right)^2}{\left(d\tau\right)^2}-\frac{\left(dz\right)^2}{\left(d\tau\right)^2}=c^2

c^2\left(\frac{dt}{d\tau}\right)^2-\left(\frac{dx}{d\tau}\right)^2-\left(\frac{dy}{d\tau}\right)^2-\left(\frac{dz}{d\tau}\right)^2=c^2

If you know about special relativity already, you might see something here. If not, let’s take a look at what these things with dτ mean. In fact, they are just derivatives with respect to proper time.

Let’s first see what dt/dτ actually is. We can solve for dτ from its definition:

c^2\left(d\tau\right)^2=c^2\left(dt\right)^2-\left(dx\right)^2-\left(dy\right)^2-\left(dz\right)^2

d\tau=\sqrt{\left(dt\right)^2-\frac{1}{c^2}\left(\left(dx\right)^2+\left(dy\right)^2+\left(dz\right)^2\right)}

Manipulating this a little bit, we can pull out the dt from inside the square root:

d\tau=\sqrt{\left(dt\right)^2\left(1-\frac{1}{\left(dt\right)^2c^2}\left(\left(dx\right)^2+\left(dy\right)^2+\left(dz\right)^2\right)\right)}

d\tau=\sqrt{\left(dt\right)^2}\sqrt{1-\frac{1}{c^2}\left(\frac{\left(dx\right)^2}{\left(dt\right)^2}+\frac{\left(dy\right)^2}{\left(dt\right)^2}+\frac{\left(dz\right)^2}{\left(dt\right)^2}\right)}

d\tau=dt\sqrt{1-\frac{1}{c^2}\left(\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2+\left(\frac{dz}{dt}\right)^2\right)}

Now, what is this sum of the squares of these time derivatives? They are simply velocities! For example, dx/dt is just the x-component of velocity. Together these three terms are simply just the total velocity (v) and we get:

d\tau=dt\sqrt{1-\frac{v^2}{c^2}}

Then, dt/dτ is simply:

\frac{dt}{d\tau}=\frac{dt}{dt\sqrt{1-\frac{v^2}{c^2}}}=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}

This square root thing we obtained is actually a very common quantity in relativity and it is called the Lorentz factor (usually denoted by γ). So, we end up with:

\frac{dt}{d\tau}=\gamma

Next, let’s look at the derivatives of the spacial components with respect to dτ. Here we’ll need another important concept of relativity, which is four-velocity. This is explained in more detail in my introductory article to SR.

The idea of four-velocity is not really anything difficult. It is simply a velocity with four spacetime components (t,x,y,z) as opposed to the normal three space components (x,y,z). Four-velocity is typically denoted by u^μ.

The normal three velocity is defined as the derivative of the spacial components with respect to time.

Similarly, four-velocity is defined as the derivative of the spacetime components with respect to proper time. So, four-velocity is simply the relativistic analogue of the regular velocity.

There is also a similar idea, which is the four-momentum (denoted by p^μ). It is almost p=mv, except that it is actually mass multiplied by the four-velocity:

p^{\mu}=mu^{\mu}

Okay, since we only need to analyse the spacial components of this, we’re going to denote them by p_i:

p_i=mu_i

And solving for u_i (you’ll see why soon):

u_i=\frac{p_i}{m}

Now, u_i here is simply the total four-velocity of the space components (for example, the x-component would be u_x=p_x/m and so on for y and z), i.e. derivatives of the space components with respect to proper time, which would be:

u_x=\frac{dx}{d\tau}=\frac{p_x}{m}

u_y=\frac{dy}{d\tau}=\frac{p_y}{m}

u_z=\frac{dz}{d\tau}=\frac{p_z}{m}

Let’s now look at the formula from earlier, which was:

c^2\left(\frac{dt}{d\tau}\right)^2-\left(\frac{dx}{d\tau}\right)^2-\left(\frac{dy}{d\tau}\right)^2-\left(\frac{dz}{d\tau}\right)^2=c^2

These are, in fact, nothing but the squares of the four-velocities! So, we can insert all of the things we derived so far like this:

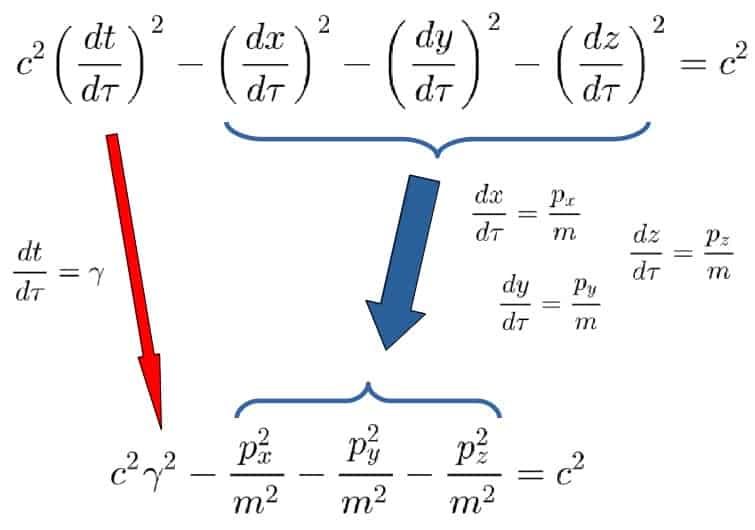
Or combining all of the momenta into one term, p_i:

c^2\gamma^2-\frac{p_i^2}{m^2}=c^2

Now, we just need to do one thing and that is to consider the relativistic total energy (not including potential energy), which is defined as follows (see in my article here):

E=\gamma mc^2

Now, let’s square that on both sides:

E^2=\left(\gamma mc^2\right)^2=\gamma^2m^2c^4

Then we can just manipulate this to get an expression for the thing in our formula, γ²c²:

E^2=\gamma^2m^2c^4

\gamma^2c^2=\frac{E^2}{m^2c^2}

Inserting this into the equation we had:

Now it’s only a matter of solving for the momentum:

\frac{E^2}{m^2c^2}-\frac{p_i^2}{m^2}=c^2

\frac{E^2}{c^2}-p_i^2=m^2c^2

p_i=\sqrt{\frac{E^2}{c^2}-m^2c^2}

From the above formula we can indeed see what happens in the case of a photon, when the mass goes to zero (forgetting about the i-index):

\lim_{m\rightarrow0}p=\sqrt{\frac{E^2}{c^2}-0^2\cdot c^2}=\sqrt{\frac{E^2}{c^2}}=\frac{E}{c}

This tells us that the momentum of a photon is proportional to its energy, which is exactly what we would expect based on experimental results.

Now, the question is; how do we actually calculate the energy of a photon if the energy is defined as E=γmc² but the mass goes to zero? Well, that requires taking a look at the quantum mechanical model of a photon.

Momentum Of A Photon According To Quantum Mechanics

If we really wish to consider the energies and momenta of particles, such as photons, we do have to take into account quantum mechanics as well. A photon is, after all, an elementary particle.

The first thing to do is to actually forget the above definition for energy, E=γmc² and rather consider a more fundamental, quantum mechanical equation for the energy.

At the turn of the 20th century, Max Planck deduced, partly by accident that the energy of electromagnetic radiation (light) was actually not continuous such as it is typically thought of, but rather comes in discrete energy packets that have energy proportional to the frequency of the electromagnetic radiation.

It was later Einstein who won the Nobel prize (through his work on the photoelectric effect) for showing that these energy packets are, in fact, massless elementary particles, which became known as photons.

Now, light consisting of these photons meant that the photons had to also have energy that is proportional to the frequency of the electromagnetic waves.

Together, the work of both Planck and Einstein can be expressed in one simple mathematical equation known as the Planck-Einstein relation, which states that the energy of a photon is given by:

E=hf

Here, f is the frequency and h is a proportionality constant that became known as the Planck constant. Determined by observations, the Planck constant has a value of around 6.63×10⁻³⁴ J⋅s.

Now, since light is still an electromagnetic wave, it obeys basic wave mechanics and so its speed (c), frequency (f) and wavelength (λ) are connected by the equation:

c=\lambda f

Or solving for f:

f=\frac{c}{\lambda}

The energy can also be expressed in terms of the wavelength by inserting this into the Planck-Einstein equation:

E=\frac{hc}{\lambda}

Now, we’re going to use the equation from earlier, which stated that the momentum of a photon is proportional to its energy (p=E/c). Connecting both the relativistic and the quantum mechanical equations, we then get:

p=\frac{E}{c}=\frac{\frac{hc}{\lambda}}{c}=\frac{hc}{\lambda c}=\frac{h}{\lambda}

This result is also known as the de Broglie relation, which connects the momentum to the wavelength of a wave (for matter waves as well, but that’s a whole different story).

So, the bottom line is that a photon indeed still has momentum even though it has no mass. The momentum of a photon can be expressed in a variety of forms.