Gradient In Different Coordinates (Intuition & Step-By-Step Examples)
The gradient is one of the most important differential operators often used in vector calculus. The gradient is usually taken to act on a scalar field to produce a vector field.
In simple Cartesian coordinates (x,y,z), the formula for the gradient is:
\nabla f=\frac{\partial f}{\partial x}\hat{x}+\frac{\partial f}{\partial y}\hat{y}+\frac{\partial f}{\partial z}\hat{z}These things with “hats” represent the Cartesian unit basis vectors.
However, in many cases, we may want to use other coordinate systems than just the Cartesian one. In other coordinate systems, the formula for the gradient will look quite a bit different.
In this article, you’ll learn how to derive the formula for the gradient in ANY coordinate system (more accurately, any orthogonal coordinate system).
You’ll also understand how to interpret the meaning of the gradient in the most commonly used coordinate systems; polar coordinates, spherical coordinates as well as cylindrical coordinates.
In this article, we’ll only look at gradients of scalar functions, but it’s worth noting that the concept of a gradient can also be extended to vector fields (through the use of a covariant derivative).
Quick tip: If you want to learn more about the gradient and other topics in vector calculus, I think you’ll really enjoy my course Advanced Math For Physics (link to the course page), which aims to give you all of the fundamental tools of vector calculus – and much more. The course is specifically focused on applications in physics, so everything you learn is aimed to be highly practical.
Table of Contents
How To Find The Gradient In Any Coordinate System (Simple Step-By-Step Method)
The general formula for the gradient of a scalar function in any orthogonal coordinate system (meaning that each of the coordinate directions are independent of one another) is:
\nabla f=\sum_i^{ }\frac{1}{h_i}\frac{\partial f}{\partial x^i}\hat{e}_iThis may look complicated, but using it is actually really simple. First, however, we can try to understand the meaning of each of these pieces here:
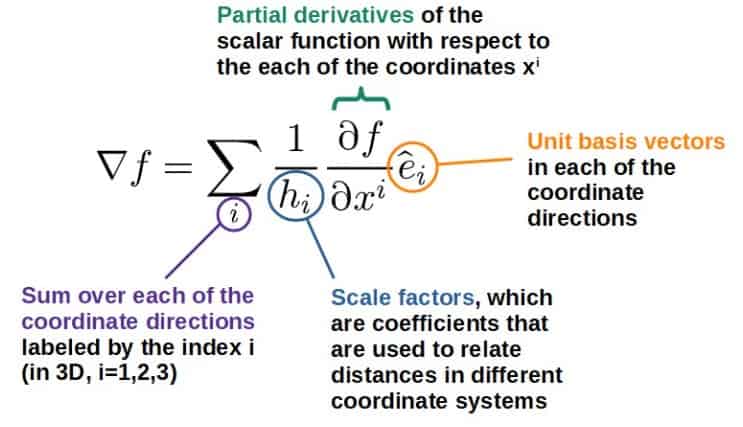
Here, each of the coordinates are labeled by a “shorthand” notation, xi, where the index i runs over as many values as there are coordinates. For example, in Cartesian coordinates, these xi‘s would be simply:
x^i=\left(x^1{,}x^2{,}x^3\right)=\left(x{,}y{,}z\right)Now, the meaning of these unit basis vectors and the coordinate partial derivatives should be quite straightforward.
However, these scale factors are something you may not have seen before. I’ll explain these soon.
The general process of calculating the gradient in any orthogonal coordinate system is then, more or less, as follows:
- Define a set of coordinates as well as unit basis vectors in each coordinate direction.
- Write down the components of the metric tensor in these coordinates.
- Calculate the scale factors from the diagonal components of the metric.
- Apply the general gradient formula using the scale factors, coordinate derivatives and unit basis vectors.
Scale Factors Explained
The first thing we need to note is that pretty much every coordinate system we may want to study has a metric tensor associated to it.
For commonly used coordinates, like polar, spherical and so on, the metric is well-known (you’ll find some examples later in the article).
In 3 dimensions, the metric can be represented as a 3×3-matrix (in 2D, we would have a 2×2-matrix as we’ll see in the case of polar coordinates). For orthogonal coordinate systems, the metric is also diagonal:
g_{ij}=\begin{pmatrix}g_{11}&0&0\\0&g_{22}&0\\0&0&g_{33}\end{pmatrix}If you don’t know much about matrices, you can pretty much just think of them as “stuff represented in a table”. A diagonal matrix has zeros everywhere except on the diagonal.
Essentially, the metric tensor is a tool used to relate coordinate displacements to lengths in various coordinate systems and spaces.
At this point, I would highly recommend checking out my full article covering the metric tensor. The article also explains what these scale factors really represent.
For our purposes, we just need to know the metric of a given coordinate system to find the scale factors. The scale factors are essentially the square roots of these diagonal metric components:
h_1=\sqrt{g_{11}}{,}\ h_2=\sqrt{g_{22}}{,}\ h_3=\sqrt{g_{33}}In other words, all the scale factors can be calculated from the metric components that have equal indices:
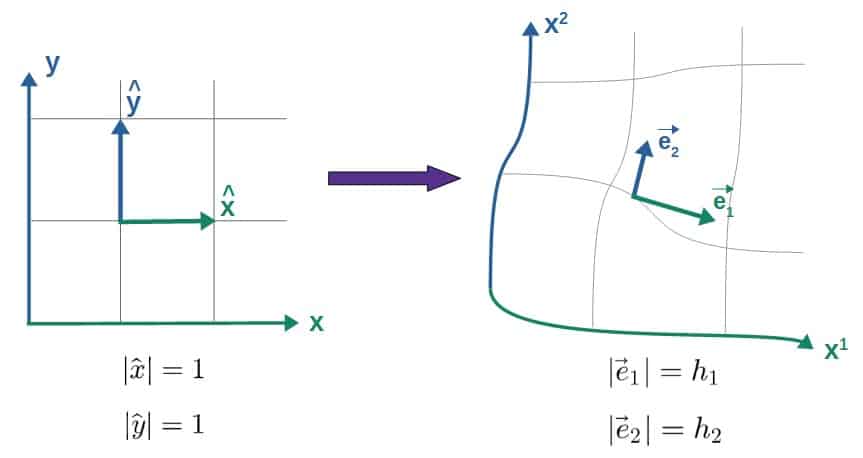
h_i=\sqrt{g_{ii}}Now, what do these scale factors actually represent? Simply put, the scale factors are the magnitudes of the basis vectors in a given coordinate system.
We’re used to having unit basis vectors (with length 1) in Cartesian coordinates, but in other coordinates, this may not always be the case.
The scale factors tell you how the lengths of the basis vectors scale when switching from, for example, Cartesian coordinates to some other coordinate system.
Before moving on to examples, I’ve included a full derivation of the gradient formula in other coordinate systems.
The derivation uses some tensor calculus and coordinate transformation stuff.
We’ll derive the general formula for the gradient in any (orthogonal) coordinate system by first looking at the gradient in Cartesian coordinates and then doing a coordinate transformation to some other, general coordinate system:
\nabla f=\frac{\partial f}{\partial x}\hat{x}+\frac{\partial f}{\partial y}\hat{y}+\frac{\partial f}{\partial z}\hat{z}I’ll now write this in a bit of a different way as a sum of these partial derivatives and the basis vectors. Here, I’ll label these Cartesian coordinates and Cartesian basis vectors with a bar as follows:
\overline{x}^i=\left(x{,}y{,}z\right)\\\vec{\overline{e}}_j=\left(\hat x{,}\hat y{,}\hat z\right)Using these, we can write the gradient in Cartesian coordinates as:
\nabla f=\frac{\partial f}{\partial x}\hat{x}+\frac{\partial f}{\partial y}\hat{y}+\frac{\partial f}{\partial z}\hat{z}=\sum_{ij}^{ }\frac{\partial f}{\partial\overline{x}^i}\vec{\overline{e}}_jNow, strictly speaking this is not really the same expression anymore and the reason is that this sum is over ALL values of i and j, so it will contain cross terms that would have, for example i=1 and j=2.
Since the Cartesian coordinate system is orthogonal, we can fix this by including an identity matrix in this sum (this is, in fact, the metric tensor for Cartesian coordinates):
\delta^{ij}=\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}You may notice that this has upstairs indices, which is just to make the following expression a valid tensor expression. However, you don’t need to pay much attention to this for now.
Using this, the gradient in Cartesian coordinates can be written as:
\nabla f=\sum_{ij}^{ }\delta^{ij}\frac{\partial f}{\partial\overline{x}^i}\vec{\overline{e}}_jIf you now write this sum out (over both i and j) and pick the corresponding metric components, you’ll get the correct gradient formula with none of the weird cross-terms.
Now, the reason we want to express the gradient like this is because in this form, we can now easily do a coordinate transformation to obtain the gradient in ANY coordinate system.
Coordinate transformations can be done by using the Jacobian matrix (Λ). In case you’re not familiar with this, I’d recommend checking out my Advanced Math For Physics -course.
Anyway, a coordinate transformation is basically done by multiplying a vector, tensor or covector with either the Jacobian or the inverse Jacobian matrix and summing over appropriate indices.
In particular, the terms in our gradient formula transform as:
\frac{\partial f}{\partial\overline{x}^i}=\sum_m^{ }\Lambda_{\overline{i}}^m\frac{\partial f}{\partial x^m}\\\delta^{ij}=\sum_{mk}^{ }\Lambda_m^{\overline{i}}\Lambda_k^{\overline{j}}g^{mk}\\\vec{\overline{e}}_j=\sum_k^{ }\Lambda_{\overline{j}}^k\vec{e}_kNow, again these “barred” things represent the Cartesian coordinates or basis vectors and the “unbarred” things represent the coordinates (xm) and the basis vectors (ek) in some other coordinate system.
Moreover, this gmk is the (inverse) metric tensor in the new coordinate system, which generally will NOT have just 1’s and 0’s.
Essentially, these relations allow us to express the Cartesian “stuff” in terms of the same “stuff” but expressed in a new coordinate system.
Using these coordinate transformation expressions, we can now write the gradient in the new coordinate system by simply inserting all of the above junk into the gradient formula:
\nabla f=\sum_{ij}^{ }\delta^{ij}\frac{\partial f}{\partial\overline{x}^i}\vec{\overline{e}}_j\ \ \Rightarrow\ \ \nabla f=\sum_{ij}^{ }\sum_{mk}^{ }\Lambda_m^{\overline{i}}\Lambda_k^{\overline{j}}g^{mk}\sum_m^{ }\Lambda_{\overline{i}}^m\frac{\partial f}{\partial x^m}\sum_k^{ }\Lambda_{\overline{j}}^k\vec{e}_kI’m going to clean this expression up a little:
\nabla f=\sum_{ij}^{ }\sum_{mk}^{ }\Lambda_m^{\overline{i}}\Lambda_{\overline{i}}^m\Lambda_k^{\overline{j}}\Lambda_{\overline{j}}^kg^{mk}\frac{\partial f}{\partial x^m}\vec{e}_kNow, here we essentially have the “products” (or more precisely, index contractions) of the inverse Jacobian and the Jacobian matrices (the Λ’s). The product (contraction) of a matrix with its inverse is just 1:
\sum_{im}^{ }\Lambda_m^{\overline{i}}\Lambda_{\overline{i}}^m=1{,}\ \sum_{kj}^{ }\Lambda_k^{\overline{j}}\Lambda_{\overline{j}}^k=1The gradient formula then reduces to:
\nabla f=\sum_{mk}^{ }g^{mk}\frac{\partial f}{\partial x^m}\vec{e}_kWe’re almost there. The real magic happens if we now make the assumption of an orthogonal coordinate system, so that the metric only has diagonal components with all off-diagonal components being zero. In this case, we can express any general diagonal metric in terms of the identity matrix as:
g^{mk}=\begin{pmatrix}g^{11}&0&0\\0&g^{22}&0\\0&0&g^{33}\end{pmatrix}=g^{kk}\delta^{mk}This δmk (which is a matrix with 1’s on the diagonal and 0’s everywhere else) essentially guarantees that the metric is diagonal as all the off-diagonal components will automatically be zero.
Now, these gkk-components are related to the scale factors by:
h^k=\frac{1}{h_k}=\sqrt{g^{kk}}\ \ \Rightarrow\ \ g^{kk}=\frac{1}{h_k^2}The scale factors with upstairs indices (hk) that are related to the inverse metric components (gkk) are just inverses of the “ordinary” scale factors.
Our gradient formula can now be expressed as:
\nabla f=\sum_{mk}^{ }g^{kk}\delta^{mk}\frac{\partial f}{\partial x^m}\vec{e}_k=\sum_{mk}^{ }\frac{1}{h_k^2}\delta^{mk}\frac{\partial f}{\partial x^m}\vec{e}_kDue to this “identity matrix”, δmk, all terms in this sum where m≠k will automatically be zero since all the values of δmk for m≠k (the off-diagonal components) are zero. Therefore, the non-zero terms in this sum all have m=k (in which case δmk=1), so this becomes:
\nabla f=\sum_{mk}^{ }\frac{1}{h_k^2}\delta^{mk}\frac{\partial f}{\partial x^m}\vec{e}_k=\sum_k^{ }\frac{1}{h_k^2}\frac{\partial f}{\partial x^k}\vec{e}_kWe need to do one last thing here. We would like to express the gradient in terms of unit basis vectors (represented with a “hat”) instead of these basis vectors ek that may have any length.
Well, we can make any basis vector have unit length by dividing by its magnitude:
\hat{e}_k=\frac{\vec{e}_k}{\left|\vec{e}_k\right|}=\frac{\vec{e}_k}{h_k}\ \ \Rightarrow\ \ \vec{e}_k=h_k\hat{e}_kHere I’ve made use of the fact that the magnitudes of these basis vectors ek are just the scale factors hk.
Inserting this into the gradient expression, we finally get the formula for the gradient in any orthogonal coordinate system:
\nabla f=\sum_k^{ }\frac{1}{h_k^2}\frac{\partial f}{\partial x^k}\vec{e}_k=\sum_k^{ }\frac{1}{h_k^2}\frac{\partial f}{\partial x^k}h_k\hat{e}_k=\sum_k^{ }\frac{1}{h_k}\frac{\partial f}{\partial x^k}\hat{e}Gradient In Polar Coordinates (Intuition + Full Derivation)
Let’s now apply the formula given above to derive the gradient in polar coordinates. Our set of coordinates, xi, is:
x^i=\left(x^1{,}x^2\right)=\left(r{,}\theta\right)The unit basis vectors are just:
\hat{e}_i=\left(\hat{e}_1{,}\hat{e}_2\right)=\left(\hat{r}{,}\hat{\theta}\right)The metric tensor for polar coordinates, expressed in matrix form is:
g_{ij}=\begin{pmatrix}1&0\\0&r^2\end{pmatrix}The scale factors, hi, are just (square roots of) the diagonal components here:
h_i=\left(h_1{,}h_2\right)=\left(\sqrt{g_{11}}{,}\sqrt{g_{22}}\right)=\left(1{,}r\right)Using the general formula for the gradient, we have (the sum only having two terms in polar coordinates):
\nabla f=\sum_i^{ }\frac{1}{h_i}\frac{\partial f}{\partial x^i}\hat{e}_i=\frac{1}{h_1}\frac{\partial f}{\partial x^1}\hat{e}_1+\frac{1}{h_2}\frac{\partial f}{\partial x^2}\hat{e}_2Inserting everything into this, the gradient in polar coordinates is:
\nabla f=\frac{\partial f}{\partial r}\hat{r}+\frac{1}{r}\frac{\partial f}{\partial\theta}\hat{\theta}Look how simple it was to derive this with the general gradient formula! The great thing is that you can use the formula for any orthogonal coordinate system you wish (we’ll see how this is done for spherical and cylindrical coordinates soon).
Before we look at more examples, let’s try to understand what the gradient in polar coordinates means intuitively speaking.
The gradient of a scalar function is essentially a vector that represents how much the function changes in each coordinate direction.
Now, in polar coordinates, the θ-basis vector originally has a length of r (not the unit vector in the above formula), meaning that its length changes as you go further away from the origin.
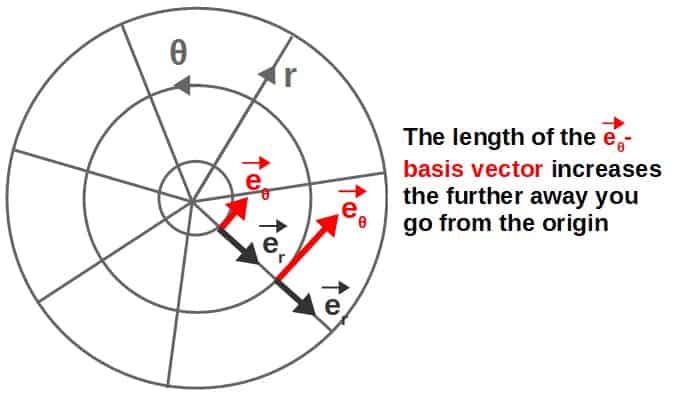
However, the gradient is used to only describe how the function f changes with respect to the coordinates (r and θ) and NOT account for how the basis vectors change.
That’s why we divide by this factor of r in the gradient formula; to get rid of the scaling of the θ-basis vector as this does not have anything to do with how the function itself changes (which is what we care about when calculating a gradient).
This then allows us to express the gradient (change in the function f) “correctly” in terms of unit basis vectors.
This also explains the intuition behind the scale factors in the gradient formula more generally; the scale factors (which describe lengths of basis vectors) are used to scale the basis vectors to have unit length.
This is necessary to give the correct results from the gradient, because it gets rid of any “incorrections” to the change in a function (which is what the gradient measures) caused by the lengths of the basis vectors changing.
Gradient In Spherical Coordinates (Intuition + Full Derivation)
In the spherical coordinate system, we have a radius and two angles as our coordinates (this is now a 3D coordinate system):
x^i=\left(x^1{,}x^2{,}x^3\right)=\left(r{,}\theta{,}\phi\right)The unit basis vectors, respectively, are simply:
\hat{e}_i=\left(\hat{e}_1{,}\hat{e}_2{,}\hat{e}_2\right)=\left(\hat{r}{,}\hat{\theta}{,}\hat \phi\right)The metric tensor for spherical coordinates is:
g_{ij}=\begin{pmatrix}1&0&0\\0&r^2&0\\0&0&r^2\sin^2\theta\end{pmatrix}The scale factors from this are then:
h_i=\left(h_1{,}h_2{,}h_3\right)=\left(1{,}r{,}r\sin\theta\right)The general formula for the gradient, in this case, is:
\nabla f=\sum_i^{ }\frac{1}{h_i}\frac{\partial f}{\partial x^i}\hat{e}_i=\frac{1}{h_1}\frac{\partial f}{\partial x^1}\hat{e}_1+\frac{1}{h_2}\frac{\partial f}{\partial x^2}\hat{e}_2+\frac{1}{h_3}\frac{\partial f}{\partial x^3}\hat{e}_3Inserting all of the spherical coordinate stuff into this, we get the gradient in spherical coordinates:
\nabla f=\frac{\partial f}{\partial r}\hat{r}+\frac{1}{r}\frac{\partial f}{\partial\theta}\hat{\theta}+\frac{1}{r\sin\theta}\frac{\partial f}{\partial\phi}\hat{\phi}Intuitively, these factors of 1/r and 1/rsinθ here again take care of the fact that the θ- and φ-basis vectors have non-unit lengths:
\left|\vec{e}_{\theta}\right|=r\\\left|\vec{e}_{\phi}\right|=r\sin\thetaThat’s why we divide by these scale factors; to get rid of the contributions to the gradient caused by the basis vector’s lengths varying (which makes the gradient only describe how the function itself changes), and to be able to express the gradient in terms of unit basis vectors.
Gradient In Cylindrical Coordinates (Intuition + Full Derivation)
In the cylindrical coordinate system, we have a radius, an angle as well as a height as our coordinates (the height being the z-coordinate, the same as in the Cartesian system):
x^i=\left(x^1{,}x^2{,}x^3\right)=\left(r{,}\theta{,}z\right)The unit basis vectors are:
\hat{e}_i=\left(\hat{e}_1{,}\hat{e}_2{,}\hat{e}_2\right)=\left(\hat{r}{,}\hat{\theta}{,}\hat{z}\right)The metric tensor for cylindrical coordinates is:
g_{ij}=\begin{pmatrix}1&0&0\\0&r^2&0\\0&0&1\end{pmatrix}The scale factors from this are then:
h_i=\left(h_1{,}h_2{,}h_3\right)=\left(1{,}r{,}1\right)The general formula for the gradient, written out, is:
\nabla f=\sum_i^{ }\frac{1}{h_i}\frac{\partial f}{\partial x^i}\hat{e}_i=\frac{1}{h_1}\frac{\partial f}{\partial x^1}\hat{e}_1+\frac{1}{h_2}\frac{\partial f}{\partial x^2}\hat{e}_2+\frac{1}{h_3}\frac{\partial f}{\partial x^3}\hat{e}_3Inserting all of the cylindrical coordinate stuff into this, we get the gradient in cylindrical coordinates:
\nabla f=\frac{\partial f}{\partial r}\hat{r}+\frac{1}{r}\frac{\partial f}{\partial\theta}\hat{\theta}+\frac{\partial f}{\partial z}\hat{z}Once again, the θ-basis vector here has a non-unit length:
\left|\vec{e}_{\theta}\right|=rTherefore, the scale factor gets rid of this and turning this into a unit basis vector by dividing with this factor of r.
However, the r- and z-basis vectors already have unit length by default, which is why the scale factors don’t do anything to the r- and z-components of the gradient.
If you want to go deeper into vector calculus and related topics, you’ll definitely enjoy my Advanced Math For Physics -course. The course has a dedicated section on understanding the gradient, divergence, curl and so forth in general coordinate systems – this article was just a surface scratch compared to what we discuss inside the course!

