Does Gravity Do Work? (With Step-By-Step Examples)
Gravity, to put it simply, is a force that causes objects to fall. Forces, on the other hand, have the ability to do work (change the energy of a system or convert it into other forms), so does this mean that gravity also does work?
In short, gravity does indeed do work for the simple reason that it converts potential energy into kinetic energy. It is important to realize, however, that gravity can only do work in the direction of the gravitational force, not for example, perpendicularly to the gravitational force.
The fact that gravity only does work in the direction of the force is a consequence of something called path independence, which is a property of all conservative forces (such as gravity).
I explain this idea in more detail in this article, but the bottom line is that path independence in the context of gravity means that the work done by gravity only depends on the total displacement in the direction of the gravitational force.
That probably sounds more complicated than it is, so let me explain it more.
Let’s say that some object, such as an orange (not an apple this time!) is falling downwards. The gravitational force will then be F=mg (mass of the orange times the gravitational acceleration).
The work done by gravity in the case where the orange simply falls downwards is W=mgh (h is the total height or distance the object falls). I’ll explain where this equation comes from later in the article.
Now, let’s take the orange moving down in a weird curved path that will be longer than just the downwards straight line (see picture down below). Will the work done by gravity then also be larger?
The surprising answer is actually no, the work that gravity does is still W=mgh, which means that the work done only depends on the total displacement in the direction of gravity (the height in this case), not the actual path itself.
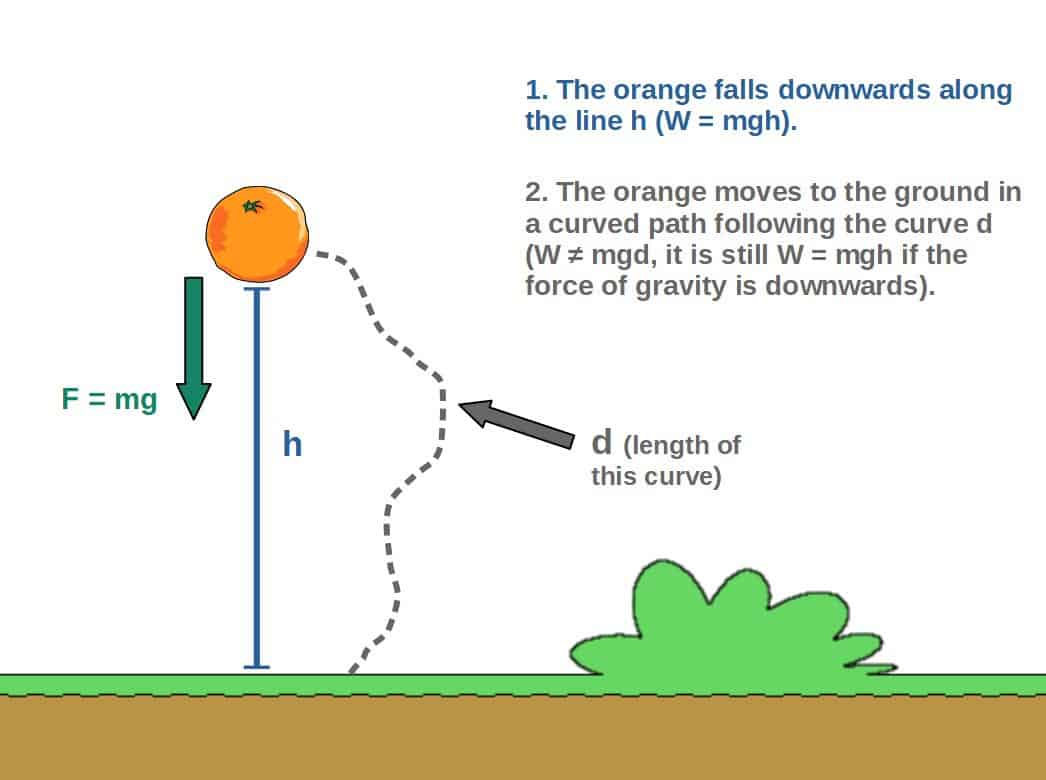
If you didn’t know this before, the idea of path independence may seem a little weird, but quite amazingly, it is an inherent property of how gravity works.
In fact, only the work done by non-conservative forces will depend on the actual path taken (see my article on conservative vs. non-conservative forces).
Also, a very helpful and understandable explanation of this property can be found in this video from Khan Academy:
Another quite interesting thing is the concept of potential energy, which in the context of gravity, is called gravitational potential energy.
In fact, gravitational potential energy is also deeply connected to the work done by gravity (which you may have noticed above from the formula W=mgh, which is the same as the formula for gravitational potential energy, U=mgh).
Let me explain. Gravitational potential energy is actually defined in terms of the work done against gravity. Here’s the technical definition:
Gravitational potential energy is defined as the amount of work needed to move an object against the force of gravity.
Now, since the potential energy is defined as the work done against gravity, the work done and the change in potential energy will always have opposite signs. This actually gives us the definition for the work done by gravity (and also for any other conservative forces):
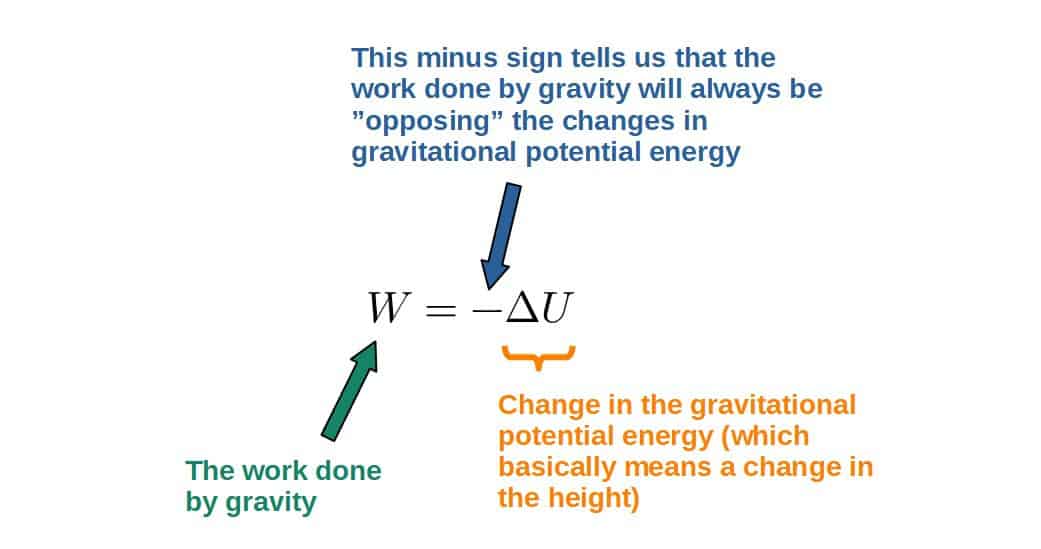
A nice example of the above definition is that say, an object is falling downwards due to gravity. Since its height will decrease, the change in potential energy will be negative.
Because ΔU is negative, the work done by gravity will be positive (opposite sign). The positive work will, in fact, correspond to an increase in kinetic energy as the object falls (I’ll explain this later).
If, on the other hand, the work done by gravity were negative, then that would correspond to a decrease in kinetic energy and an increase in potential energy (this is seen in, for example, when a ball is thrown upwards; its speed will go down and its height will increase).
The work done by gravity can also be expressed in terms of the change in kinetic energy (notice that they now have the same sign; the work will be positive if the kinetic energy increases and vice versa):
W=\Delta TI’m denoting kinetic energy by T, which is a common convention in Lagrangian mechanics.
From this, we can also say that the change in kinetic energy will be the same as the change in potential energy, but with opposite sign (the increase in kinetic energy has to be the same as the decrease in potential energy):
\Delta T=-\Delta UAnyway, the key takeaways here, before we move on to some concrete examples, are the following:
- Gravity does work whenever an object moves in the direction of the gravitational force.
- The work done by gravity depends only on the total displacement in the direction of the gravitational force.
- The work done by gravity corresponds to potential energy being converted into kinetic energy or vice versa.
Quick tip: For building a deep understanding of the most important mathematical tools used in physics as well as calculus-based physics in general, I’d highly recommend my Advanced Math For Physics -course (link to the course homepage) as I think this is the perfect resource on these topics for someone wanting to learn advanced physics.
This course is ideal for beginners (for both self-studying and students) who want to study physics at a deeper level, but don’t know exactly where to start. You will learn everything you need to know about vectors, differential and integral calculus as well as many more advanced topics in vector calculus that not many university courses will even cover. This is done through clear and intuitive explanations, LOTS of practical examples as well as practice problems you can do yourself.
How To Calculate The Work Done By Gravity (Step-By-Step Examples)
In this section, I’m going to show a bunch of actual practical examples of how the work done by gravity can be calculated. This is done in a step-by-step manner, but feel free to try them yourself first as exercises.
Anyway, the only formula we will really need here is the definition for work, which in the case of gravity is actually quite simple (in more complex cases, the definition for work generally involves integral calculus).
The work done by gravity can be calculated with the formula:
W=F\Delta r\cos\theta
, where F is the gravitational force, Δr is the total displacement and θ is the angle between the force and the displacement.
From this definition, it is clear that the work done by gravity is zero in the perpendicular direction to the displacement; if the force and displacement are perpendicular, it means that θ=90° and cos(90°)=0, so the work done would also be zero.
Quick tip: To fully understand where the above formula comes from, I’d highly recommend checking out my course Advanced Math For Physics that covers both the basics and some much more advanced stuff. You can find the course here.
First of all, to understand the formula we will use for the examples down below, we’ll have to use the most general definition for work, which is the line integral of the dot product between a given force F and a displacement vector dr:
W=\int_C^{ }\vec{F}\cdot\vec{dr}Now, what does this formula actually mean? Think of it this way; there is an object travelling along some given path C, along which the force may vary (which is why we have to use integration here).
The instantaneous work done by the force at a single point on the path is defined as the dot product between the force F and an infinitesimal displacement dr (this is a definition, it isn’t derived from anywhere!).
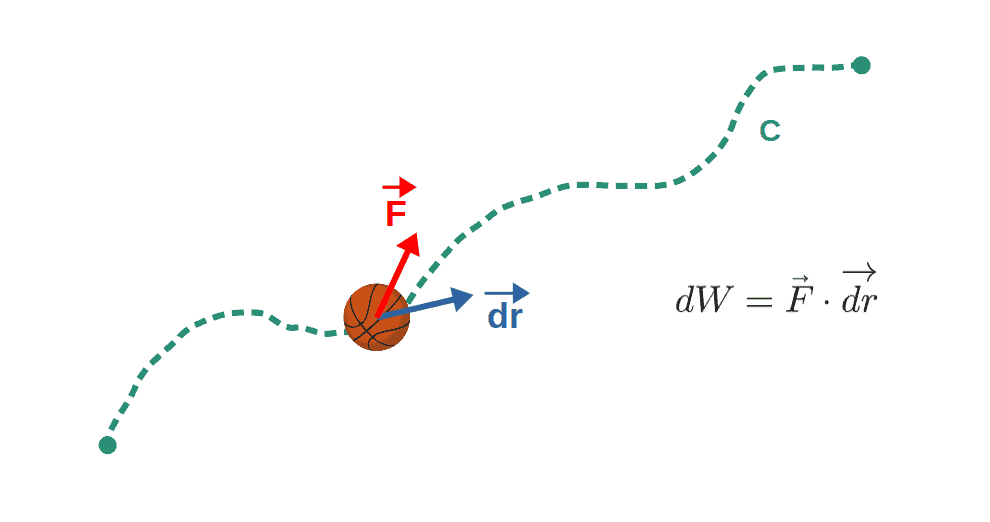
Then the total work done along the whole path C can be obtained by summing up (i.e. integrating) the instantaneous work done at each point, which is just the line integral given earlier.
Now, in the case of the force being the gravitational force, we know that the work done should only depend on the start and end points of the path (remember the path independence property).
Let’s call these points r1 and r2. Now, instead of having a path integral, we simply have an integral only between the start and end points:
W=\int_{r_1}^{r_2}\vec{F}\cdot\vec{dr}In the case of gravity, if we’re reasonably close to the surface of the Earth, the gravitational force will be a constant. Next, we’ll use the definition for the dot product between two vectors, which is (see Wikipedia, for example):
\vec{F}\cdot\vec{dr}=Fdr\cos\thetaHere F and dr are the magnitudes of the vectors and θ is the angle between them.
Inserting this into the integral above (and moving the constants F and cosθ outside the integral sign), we get:
W=F\cos\theta\int_{r_1}^{r_2}drThis is, of course, the simplest possible integral to calculate, which will give us:
W=F\cos\theta\left(r_2-r_1\right)=F\Delta r\cos\thetaIn the examples down below, we will indeed see exactly how the idea of path independence works in practice and also how the work done by gravity turns out to always depend on simply the total displacement (change in potential energy).
Example: Work Done By Gravity On a Falling Object
It is known that gravity is what causes an object to fall, which means that the potential energy of the object will change. So, does gravity do work on a falling object then?
To put it simply, gravity does do work on every object that is falling due to gravity. The work done by gravity on a falling object depends only on the total change in height, given by the formula W=mgh. If an object is not falling (its height doesn’t change), gravity does not do any work on it.
The proof for this is extremely simple. Here’s a picture of the situation:
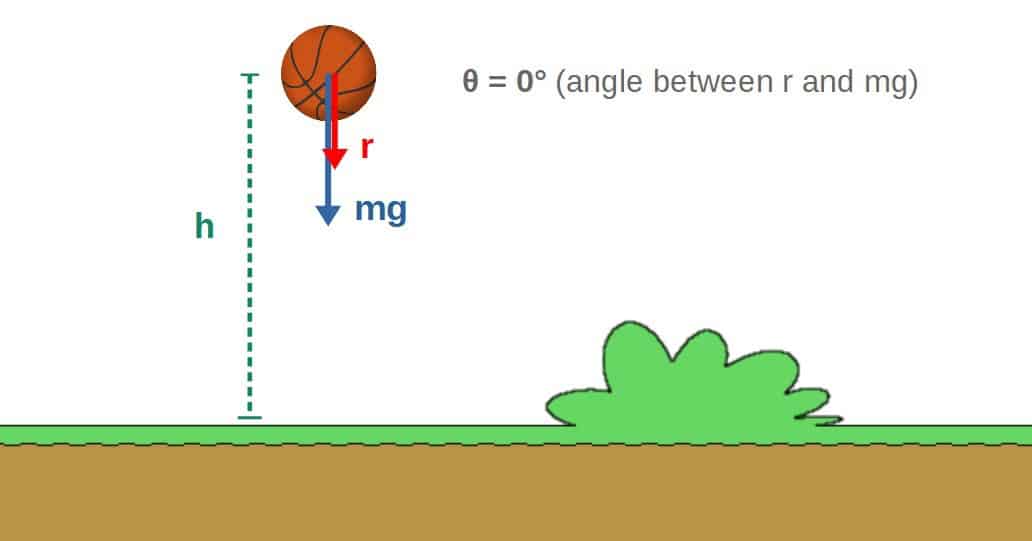
The total displacement (Δr) is simply the height h and the force will be the gravitational force F=mg. We also know that the angle θ is zero, which means that cos(0°)=1.
Inserting all of these into the formula for work (W=FΔrcosθ), we get that the work done by gravity on a falling object is W=mgh.
Work done by gravity on a falling object:
W=mgh
Example: Work Done By Gravity On an Inclined Plane
Let’s say that there is an object placed on an inclined plane. The object will start rolling down the plane due to gravity pulling it downwards, so does gravity then do work also on an inclined plane?
In short, gravity does do work on an inclined plane, however, it will only depend on the total change in height. In other words, the work done by gravity on an inclined plane is given by the formula W=mgh, which is actually the same as the work done by gravity on a simple freely falling object.
But how exactly is that possible? Shouldn’t the work also depend on the angle of the incline or something? Well, it actually turns out that it doesn’t. Let’s look at why.
Here’s a picture of the situation:
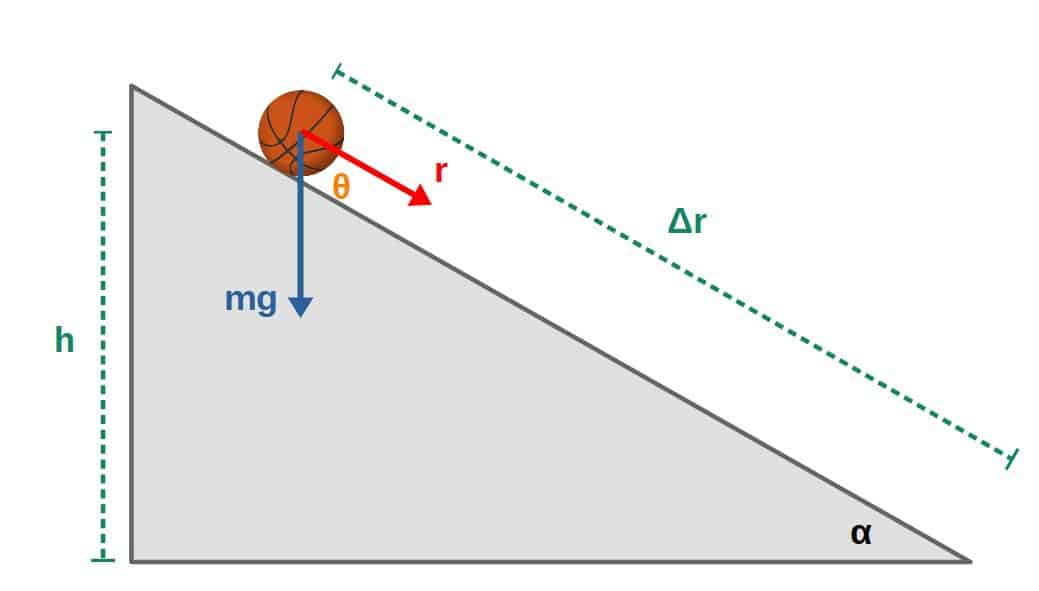
What you’ll find after a little bit of math is that the work done by gravity will actually be the same as in the case of a simple freely falling object, W=mgh.
Work done by gravity on an inclined plane:
W=mgh
To find the work done by gravity on the inclined plane as shown above, we use the formula that I gave earlier:
W=F\Delta r\cos\thetaThe force F is just the gravitational force F=mg:
W=mg\Delta r\cos\thetaWe can actually manipulate the above equation a little bit and see that it simplifies to a quite nice form.
From the inclined plane triangle, we can see that the angle between Δr (distance the object rolls down) and h (the total change in height of the object) is clearly θ (see picture from above) and from that, we can find the expression for cos(θ):
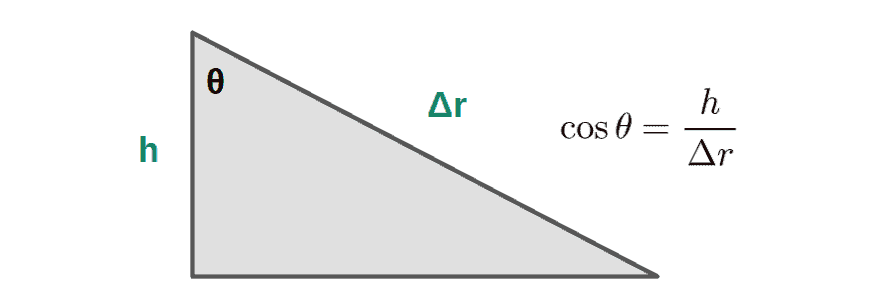
From this, simply multiply by Δr and we have:
\Delta r\cos\theta=hThe formula for the work done then becomes:
W=mg\Delta r\cos\theta=mghThe really interesting thing about the above formula is that the work done by gravity does not actually depend on the incline of the plane at all; it only depends on the total displacement in the direction of the gravitational force, i.e. the change in height.
Example: Work Done By Gravity On a Pendulum
A pendulum is a system where a mass (a pendulum “bob”) is swinging back and forth under a gravitational force. Since the force of gravity is acting on the pendulum, does gravity also do work on a pendulum?
In short, gravity does do work on a pendulum for the simple reason that the height of the pendulum bob changes. The work that gravity does on a pendulum depends only on the total displacement of the pendulum bob as measured from the ground (height of the bob) and is given by the formula W=mgh.
Here is essentially what is happening; a pendulum starts swinging from some height h and we wish to calculate what the work done by gravity on this pendulum would be (everything we need is in the picture below).
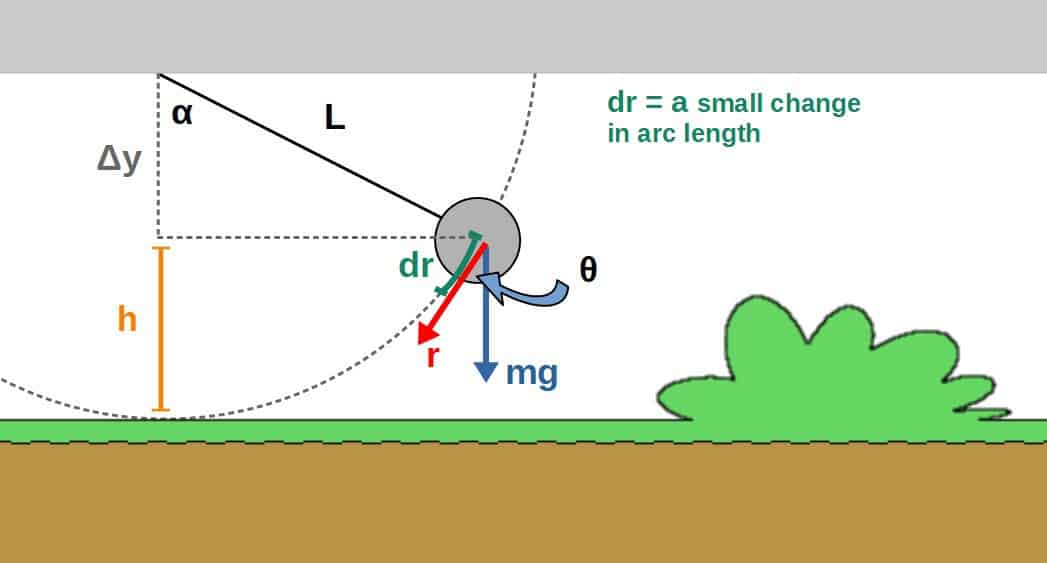
The first thing we’ll do is notice that there is actually a relationship between the angles α and θ, which can be seen from the picture down below:
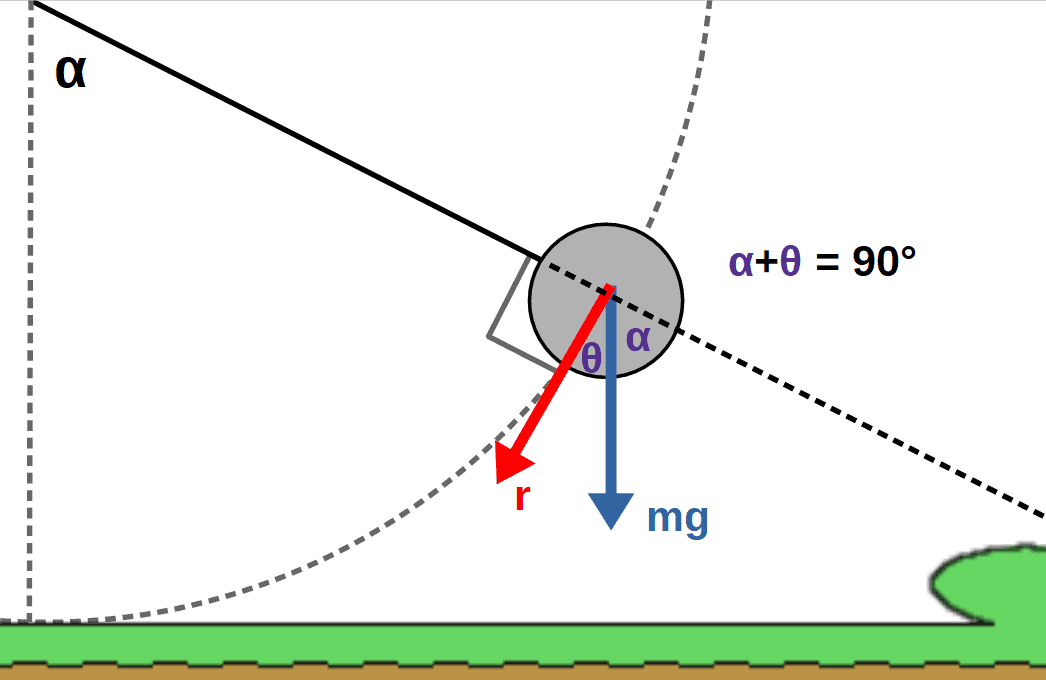
From this, we can get:
\theta+\alpha=90°\ \ \Rightarrow\ \ \ \theta=90°-\alphaWe can also find the displacement of the pendulum bob, which is simply the arc length as given by the picture below. For later purposes, we’ll want to use an infinitesimal displacement dr instead of the Δr we used earlier.
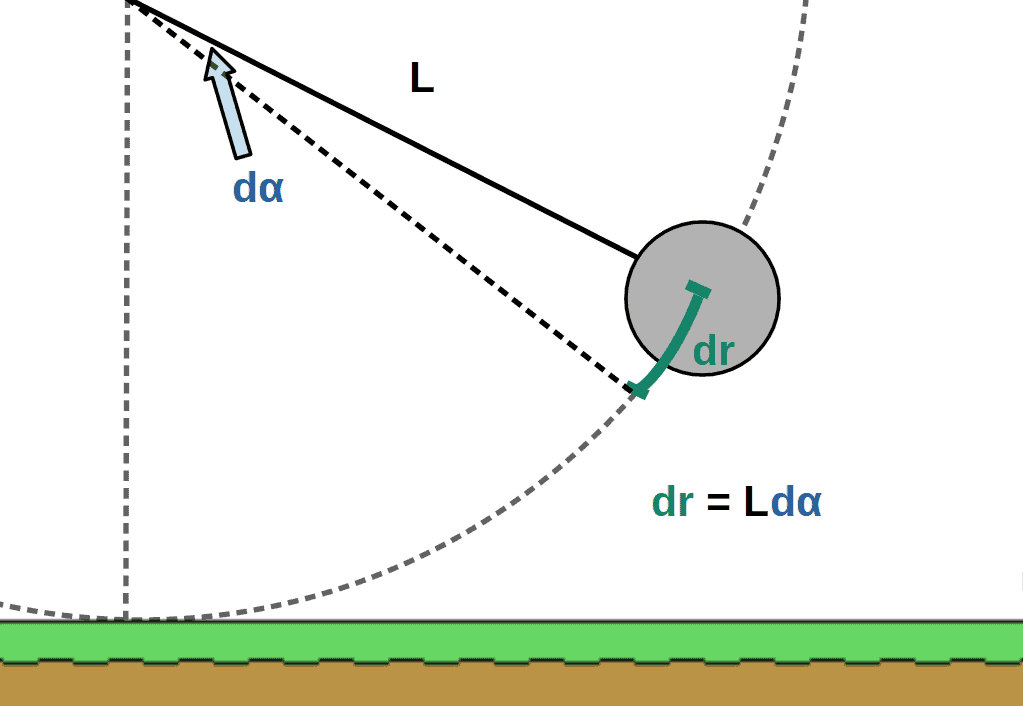
Since the pendulum is swinging and is generally a little bit more of a complicated system than the previous examples, the easiest method to find the work done by gravity is to simply start from the definition of work (see earlier if you don’t remember this):
W=\int_{r_1}^{r_2}\vec{F}\cdot\vec{d}r=\int_{r_1}^{r_2}Fdr\cos\thetaNow, dr is just the arc length from the picture above (dr=Ldα). We can also use the relationship between θ and α to get another expression for the cos(θ) -term:
\cos\theta=\cos\left(90°-\alpha\right)\ \ \ \ \ \parallel\theta=90°-\alphaIf you know any trigonometric relationships between sines and cosines, you’ll know that this is actually the same as simply sin(α).
Therefore, inserting the above equations (dr=Ldα and cos(θ)=sin(α) as well as the gravitational force F=mg), we get that the work done is (notice that we have to change the integration limits as well; we’re now integrating from the initial angle α to 0, where the pendulum is completely vertically):
W=\int_{r_1}^{r_2}Fdr\cos\theta=mgL\int_{\alpha}^0\sin\alpha d\alphaThis is a basic trigonometric integral, from which you get after evaluating the limits of integration:
W=mgL\int_{\alpha}^0\sin\alpha d\alpha=mgL\left(\cos\alpha-1\right)We’re almost done now. We can still manipulate this equation a little bit by using the following fact from the picture:
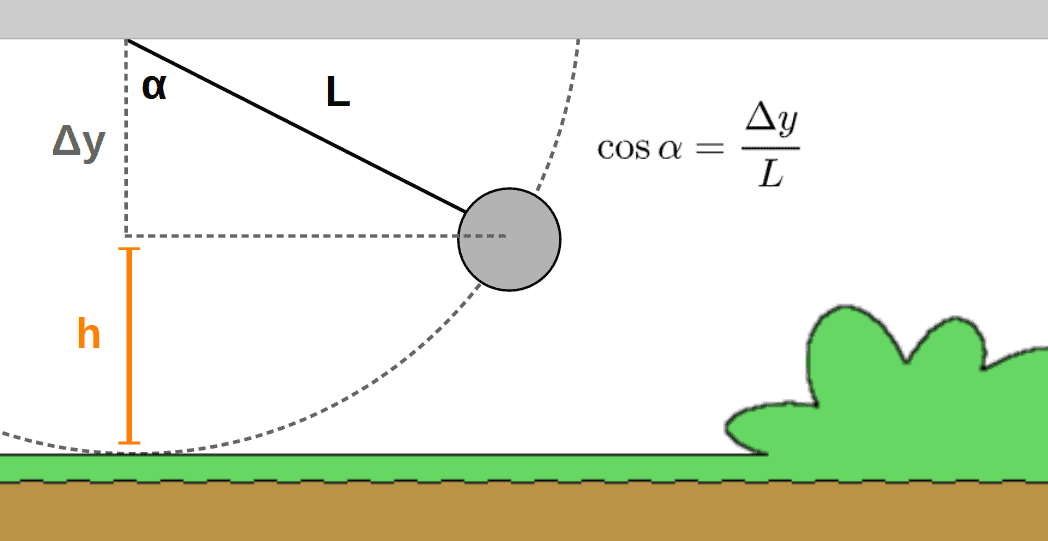
Inserting this, we get:
W=mgL\left(\cos\alpha-1\right)=mgL\left(\frac{\Delta y}{L}-1\right)=mg\left(\Delta y-L\right)Now, what is Δy – L? We know that Δy+h=L, which can be seen when the pendulum is in the vertical position. From this, we get:
\Delta y-L=-h W=mg\left(\Delta y-L\right)=-mghIf we now take the positive direction to be downwards as we’ve done with all of the previous examples as well, this then becomes the usual work done by gravity:
W=mghThe pendulum may seem like a complicated system, but again, the work done by gravity is just mgh. In the above proof, however, it was worth going through the calculation in explicit detail even though the result may not be too surprising at this point.
Now, the question you may have is; where does this work that the gravitational force does actually go? The answer is that it transforms into kinetic energy for the pendulum bob, which means that its velocity will increase.
The specific amount that the bob gains in kinetic energy will equal the work done by the gravitational force (this is just simple energy conservation).
At the bottom, all of the potential energy will have turned into kinetic energy, which means that the work done by gravity is equal to the kinetic energy of the pendulum bob (in our case, the bob will start at rest from some height h, so the initial velocity will be zero):
W=\frac{1}{2}mv^2The work done is, as calculated earlier, simply W=mgh, so we get:
\frac{1}{2}mv^2=mghFrom this, we could solve what the velocity will be at the bottom:
v=\sqrt{2gh}Now, we know that a pendulum is supposed to swing back and forth dynamically, so really this kinetic energy will turn into potential energy again once the pendulum swings back up to its maximum height (the maximum height will be the same as the initial starting height!).
These dynamic changes between potential and kinetic energy then repeat (forever in an ideal case, where air resistance doesn’t exist) and this is, in fact, what causes the pendulum to swing back and forth.
Example: Work Done By Gravity On a Satellite Orbiting Earth
When satellites are launched into space, they are put into orbit around the Earth where the gravitational force of the Earth keeps them in that orbit. Therefore, does gravity do work on a satellite orbiting the Earth?
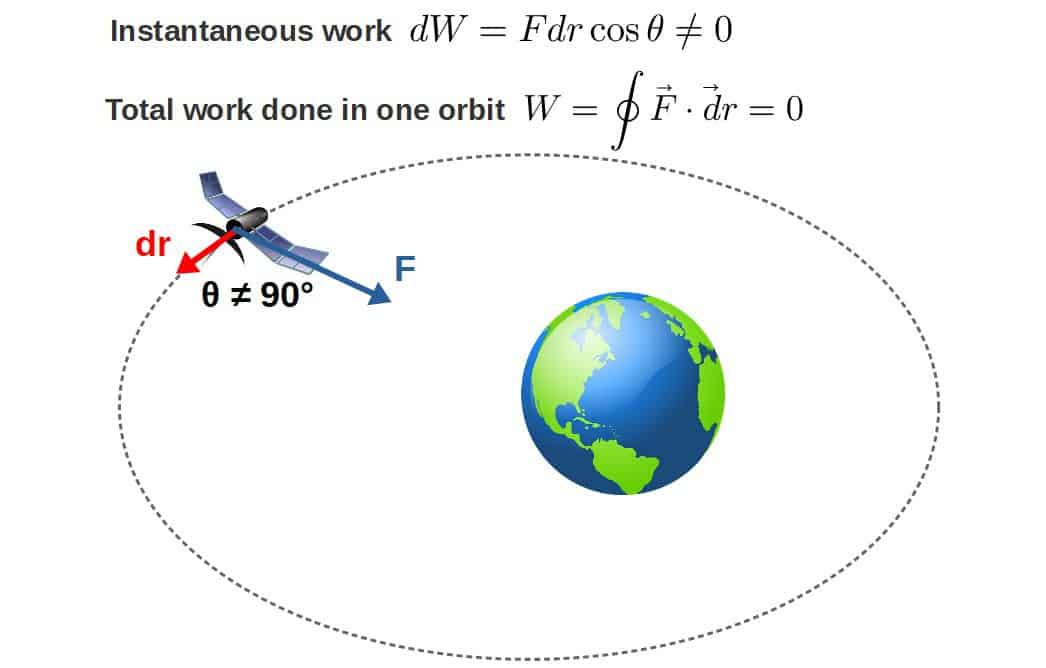
Gravity does not do work on a satellite orbiting the Earth in a circular orbit due to the displacement of the satellite being perpendicular to the force of gravity. In an elliptical orbit, however, gravity does do work on a satellite around a small arc, but the total work done around a full orbit is zero.
First of all, let’s look at the case of a circular orbit (which is an idealized scenario; real orbits usually have more or less an elliptical shape).
In a circular orbit, the gravitational force is always pointing to the center of the Earth and the direction of the displacement is always tangential.
Therefore, the angle between the force and the displacement vectors is always 90° and the work done by gravity on the satellite orbiting in a circular orbit is zero.

Now, real orbits are not perfectly circular due to various different factors. In reality, they are elliptical. In an elliptical orbit, the direction of motion is NOT always perpendicular to the force of gravity, which means that the work done by gravity may not be zero either.
Really what this means, though, is that the work done by gravity on the satellite is non-zero during a small part of the orbit (the instantaneous work, if you will).
The total work done in a full orbit still remains zero, which ultimately has to do with the conservation of angular momentum in stable orbits, whether those be elliptical of circular.