Conservative vs Non-Conservative Forces: The Key Differences

In Newtonian physics, there are generally two types of forces; conservative forces and non-conservative forces. The classification between these two types of forces is made because of a few key differences between them.

In short, conservative forces are derived from a potential, while non-conservative forces are not. Conservative forces are also path independent and conserve total energy, while non-conservative forces are path dependent and do not conserve total energy.

Here is a little comparison table of the two forces:

Conservative Forces	Non-Conservative Forces
Can be expressed in terms of a potential	Cannot be expressed in terms of a potential
Conserve energy	Do not conserve energy
Path independent	Path dependent
Always have zero curl	Have a non-zero curl
Examples: gravitational force, electrostatic force	Examples: friction, air resistance, induced emf

In the following sections each of these differences will be explained in much more detail. We’ll also discuss an easy method to practically determine whether any force is conservative or not.

Table of Contents

Conservative Forces and Potential Energy

One of the key differences between conservative and non-conservative forces is that a conservative force can always be associated with a potential energy, while a non-conservative force cannot.

So, if we have a conservative force, we can always come up with a potential that could be associated with this force.

Let’s look at exactly how we can associate a potential with a conservative force and then discuss why this cannot be done for a non-conservative force.

In case any of the mathematical concepts in this article seem unfamiliar to you, I’d highly recommend checking out my online course Advanced Math For Physics. The course covers everything from basic calculus all the way up to some of the most foundational concepts and tools used all throughout classical mechanics, electrodynamics and even relativity, in a way that anyone will be able to understand them. You’ll also get to discover how all of the mathematical tools can be directly applied to physics through intuitive step-by-step examples as well as workbooks with tons of practice problems.

Relationship Between a Conservative Force and Potential Energy

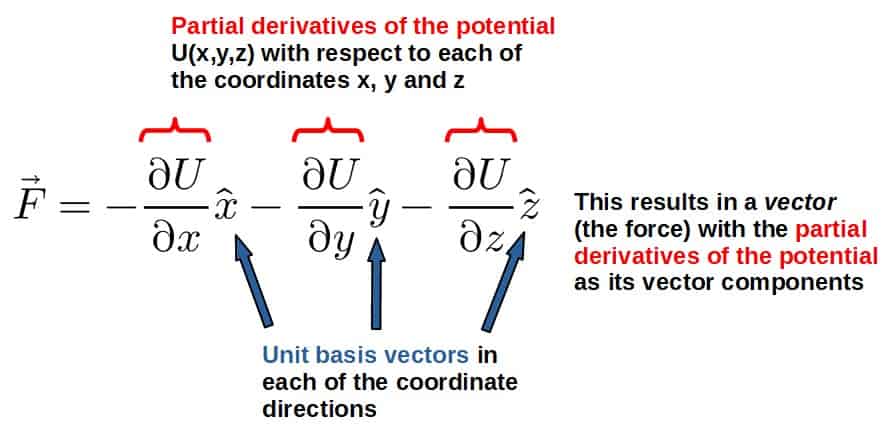
The relationship between a conservative force and potential energy is that a conservative force is defined as the negative gradient of a potential associated with that force. Mathematically, any conservative force can be expressed through this relationship as F=-∇U.

Now, a gradient is an operator in vector calculus that acts on a scalar function (the potential in this case) and gives a vector as a result (the force):

\vec F=-\vec \nabla U

The potential energy U here is generally a function of position (which in 3D Cartesian coordinates would be U(x,y,z)) and so is the force.

So, to actually calculate this gradient of the potential, we take partial derivatives of it with respect to each position coordinate and then form a vector (the force) as follows:

Geometrically, the gradient of any scalar function represents the direction in which the scalar function is changing the fastest.

If we visualize the scalar function (potential energy) as a “hill” with the height describing its value, then the gradient of the potential would be a vector that points in the “steepest” direction along the hill:

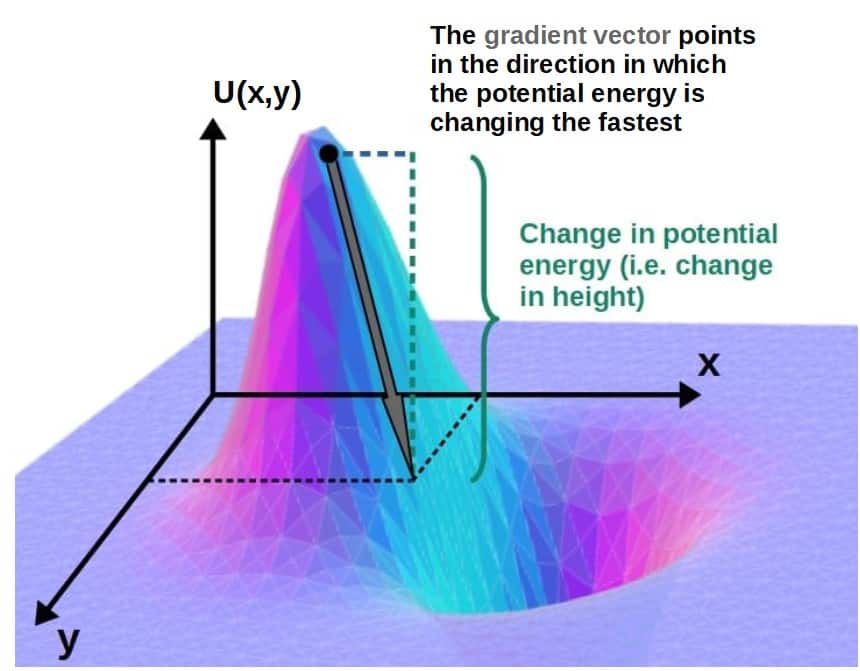
Here, we have a potential that’s a function of x and y only so that it can be visualized as a “hill”.

Now, since the force is defined as the negative gradient of the potential energy, it always points in the direction in which the potential energy is decreasing the fastest.

Physically, we can interpret this by imagining that we place a particle in some potential. The (conservative) force due to this potential would then “push” the particle in a direction such that its potential would be the lowest (the direction of greatest decrease).

Perhaps this property sheds some light to the fact that most objects in nature tend to behave in such a way that their potential is minimized.

This can be seen, for example, in a gravitational field, but also in the energy states of electrons in an atom (notice also that these are examples of conservative forces, namely the gravitational force and the electrostatic force).

Now, you may want to ask; why exactly can a conservative force be defined in terms of the gradient of a potential?

Well, this is actually a consequence of a much deeper result in vector calculus; a path independent vector field can always be written as the gradient of some scalar field.

In this case, the vector field would be the force and the scalar field would be the potential. We’ll talk more about path independence later in this article, but essentially, all conservative forces are path independent.

This definition also works mathematically; the curl of any conservative force is zero, but so is the curl of the gradient of any scalar function. Therefore, we can also say that any conservative force can be written as the gradient of some scalar function.

In fact, this also gives us a nice way to check whether a force is conservative or not by taking the curl of the force (we’ll discuss this later). The curl is essentially a vector operator that is also defined in terms of partial derivatives.

Practical Example: Gravitational Force and Potential Energy

The gravitational potential energy between two masses (M and m) is:

U=-\frac{GMm}{r}

Here, r is the distance between the two masses, which we can express, using the Pythagorean theorem, as:

r=\sqrt{x^2+y^2}

I’m assuming that the situation is in the 2-dimensional xy-plane, but you can equivalently repeat the calculation for 3-dimensions, in which case you’d have r²=x²+y²+z².

So, the potential energy is:

U=-\frac{GMm}{\sqrt{x^2+y^2}}

This is now in a form which we can easily take the gradient of. If we take the partial derivatives of this with respect to both x and y, we get:

\frac{\partial U}{\partial x}=-GMm\frac{\partial}{\partial x}\left(x^2+y^2\right)^{-\frac{1}{2}}=-GMm\left(-\frac{1}{2}\right)\left(x^2+y^2\right)^{-\frac{3}{2}}\cdot2x

Here, I’m essentially just using the power rule for derivatives as well as the chain rule.

So, the partial derivative with respect to x is then:

\frac{\partial U}{\partial x}=GMm\frac{x}{\left(x^2+y^2\right)^{\frac{3}{2}}}

Similarly, for y you would get:

\frac{\partial U}{\partial y}=GMm\frac{y}{\left(x^2+y^2\right)^{\frac{3}{2}}}

The gravitational force, using these would then be:

\vec{F}=-\vec{\nabla}U=-\frac{\partial U}{\partial x}\hat{x}-\frac{\partial U}{\partial y}\hat{y}=-GMm\frac{x}{\left(x^2+y^2\right)^{\frac{3}{2}}}\hat{x}-GMm\frac{y}{\left(x^2+y^2\right)^{\frac{3}{2}}}\hat{y}

Here, we simply have the gradient in two dimensions.

We can write this as:

\vec{F}=-\frac{GMm}{\left(x^2+y^2\right)^{\frac{3}{2}}}\left(x\hat{x}+y\hat{y}\right)

This may not be in the form you’re used to seeing it (this is really Newton’s law of gravity in disguise). We can get this into a simpler form by switching to polar coordinates (r and θ), which are defined in terms of Cartesian coordinates as follows:

x=r\cos\theta{,}\ y=r\sin\theta

Inserting these into the force equation (and also using the fact that x²+y²=r²), we get:

\vec{F}=-\frac{GMm}{\left(r^2\right)^{\frac{3}{2}}}\left(r\cos\theta\hat{x}+r\sin\theta\hat{y}\right)=-\frac{GMm}{r^2}\left(\cos\theta\hat{x}+\sin\theta\hat{y}\right)

Here, I’ve used the fact that (r²)^3/2=r³ and I’ve pulled out a common factor of r from inside the parentheses, which together cancel out to give this 1/r²-factor.

Now, it’s convenient to define this thing in the parentheses as a unit basis vector that points in the direction of the force (this is actually the definition of the radial unit vector in polar coordinates):

\cos\theta\hat{x}+\sin\theta\hat{y}=\hat{r}

Doing this, we get the usual form of Newton’s law of gravity:

\vec{F}=-\frac{GMm}{r^2}\hat{r}

Now, the point of all of this was to just show you how this relationship between potential energy and a conservative force can be used in practice.

Now, the important thing about all of this is that only conservative forces can be associated with a potential energy. The situation changes a bit if we now consider non-conservative forces, but we have to first discuss the notion of path independence.

Path Independent vs Path Dependent Forces

One of the important differences between conservative and non-conservative forces is that conservative forces are path independent, while non-conservative forces are path dependent.

Essentially, these are statements about the work done by a force on an object that moves along some particular path.

More precisely, if the force acting on an object is conservative (path independent), then the work done on this object when it moves along any path will only depend on the start and end points of the path, not the actual path itself.

On the other hand, if the force is non-conservative, then the path will also matter, not just the start and end points.

This may be best understood by a little thought experiment; we have an orange that falls down under the influence of Earth’s gravity (the gravitational force being F=mg) along two different paths; a straight down path and a weird curved path.

Along the straight path, the orange falls down a distance h (height), so the work done by gravity is W=mgh. But is the work done by gravity along the curved path W=mgd (if d is the length of the path)?

Well, the answer is actually no. The orange still falls down a height h even though it moves in some complicated curved path, so the work done is still going to be W=mgh.

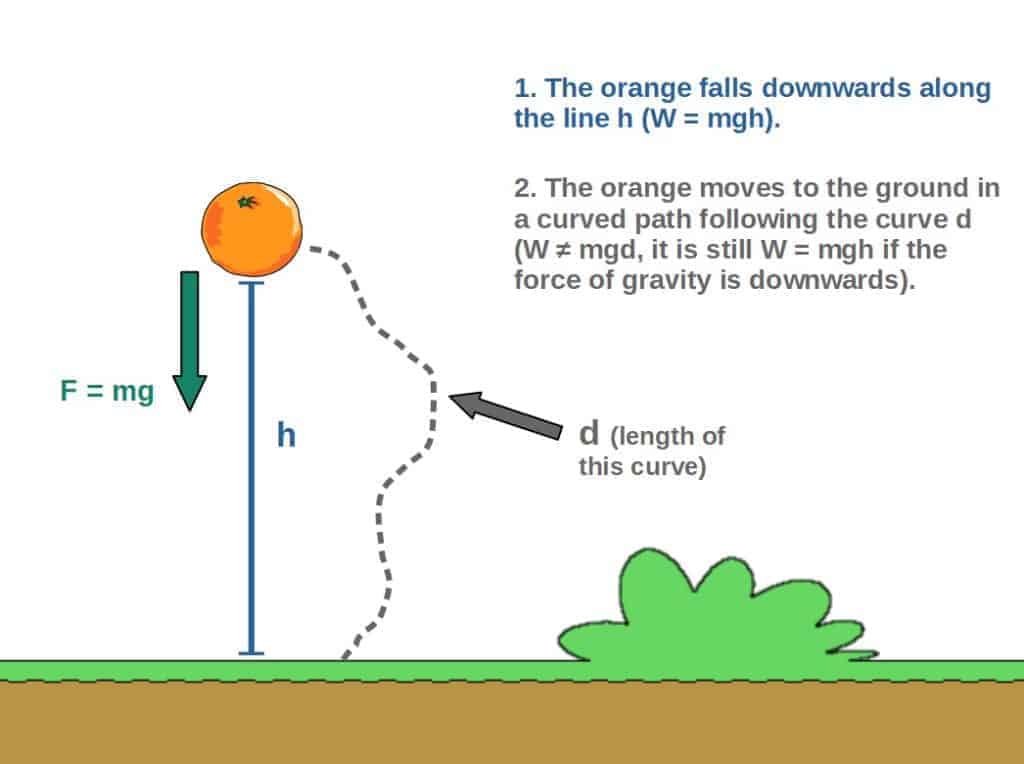
This image has an empty alt attribute; its file name is image-9-1024x764.jpg

Now, this illustrates the concept of path independence; since gravity is a conservative force, in both cases the orange falls from the same starting point to the same point on the ground and the work done only depends on what these start and end points are.

I demonstrate how to actually calculate work done by gravity in different situations (such as for a gravitational pendulum) in this article, so if you’re interested, I recommend giving it a quick read.

If we now were to imagine that there is air resistance (a non-conservative force), then the situation changes; now the work done will depend on the path due to the fact that kinetic energy is now being “lost” to air resistance.

So, for different paths, different amounts of kinetic energy will be lost. This is an example of the property of path dependence for non-conservative forces.

Now, in general, one way to mathematically state the property of path independence of a conservative force is to say that the work done around any closed path is zero:

W=\oint_C\vec{F}\cdot d\vec{r}=0

What does this actually mean? This is simply the formula for the work done around a closed path C (represented by this little “loop” around the integral sign); we’re integrating (adding up) the force F and the little displacement dr at each point along the path.

By the way, I actually have a lesson on line integrals and some of their applications to physics in my vector calculus course, which you can currently get FREE access to from this page.

Anyway, the work done being zero around a closed path is simply due to the fact that the force is conservative, in which case the work done will always be zero around such a closed path (there’s a proof of this later in the article).

On the other hand, for a non-conservative force (which I’ll denote here by little f), the work done around a closed path C will generally not be zero:

W=\oint_C\vec{f}\cdot d\vec{r}\ne0

A common misconception arising from this is that if we find some closed path where the work done is zero, then the force would automatically be conservative.

This is not true, since for a conservative force, it has to be true for ALL possible closed paths that the work done is zero. Therefore, it is NOT sufficient to just look at some specific path, but rather, it has to be true for all possible closed paths.

Therefore, it is possible for the work done by a non-conservative force to be zero around one closed path, but it’s generally not the case for ALL closed paths.

Now, just to recap, here are the key takeaways:

Conservative forces are path independent. This means that the work done by a conservative force along any path only depends on the end points of the path, not the path itself.
Non-conservative forces are path dependent. This means that the work done by a non-conservative force along a path will depend on which path is taken.
An equivalent way of stating the above is by saying that the work done by a conservative force around any closed path is zero, while the the work done by a non-conservative force around a closed path will generally not be zero.

Why Is The Work Done By a Conservative Force Path Independent? (A Simple Proof)

To show that work done by a conservative force is path independent can be done using Stokes’ theorem. This works for the simple reason that any conservative force can be written as the gradient of a potential, which results in the right-hand side of Stokes’ theorem being zero, indicating path independence.

The full proof of this can be found below.

Mathematical Proof of The Path Independence of Conservative Forces

A fairly simple way to show this is by applying Stokes’ theorem, which states that the line integral of any vector field around a closed path can be found by integrating the curl of the vector field over the surface that this closed path happens to enclose:

\oint_C\vec{F}\cdot d\vec{r}=\int_{ }^{ }\int_S^{ }\left(\vec{\nabla}\times\vec{F}\right)\cdot d\vec S

The S here denotes the particular surface that this closed path C encloses. This dS-vector is simply a way to represent the surface using a vector, which is technically normal to the surface.

The nice thing is that we do not actually need to know any details about Stokes’ theorem here. All we need to know is that generally, the curl of the gradient of any scalar function is zero.

Now, since any conservative force can be written as the negative gradient of a potential (scalar function), it directly follows that also the curl of any conservative force has to be zero:

\vec{\nabla}\times\vec{F}=\vec{\nabla}\times\left(-\vec{\nabla}U\right)=0

So, we then get that the right-hand side of Stokes’ theorem is zero for any conservative force:

\oint_C\vec{F}\cdot d\vec{r}=\int_{ }^{ }\int_S^{ }\left(\vec{\nabla}\times\vec{F}\right)\cdot d\vec{S}=0

This then proves the property that the work done by a conservative force around a closed path is zero. However, does this prove that the work done generally depends only on the end points of a path for any path, not just a closed one?

Well, it actually does! The statement that the work done is zero around a closed path is enough to say that the work done only depends on the end points of the path.

This can be done easily by imagining that we divide the closed path into two parts, such that the parts are connected together:

The path C₁ here is the path an object moves from A to B and C₂ is the path the object moves back from B to A. Thus, the paths C₁ and C₂ together form a closed path.

The total work done is just the sum of the work done along path C₁ and the work done along C₂:

W=W_1+W_2=0

Or written in terms of the line integrals:

\oint_C\vec{F}\cdot d\vec{r}=\int_{C_1}^{ }\vec{F}\cdot d\vec{r}+\int_{C_2}^{ }\vec{F}\cdot d\vec{r}=0

Now, imagine that we reverse the direction of the path C₂, such that it would now be going from A to B instead of B to A. The path itself remains the same, but we get a minus sign:

\int_{C_1}^{ }\vec{F}\cdot d\vec{r}-\int_{C_2}^{ }\vec{F}\cdot d\vec{r}=0\ \ \Rightarrow\ \ \int_{C_1}^{ }\vec{F}\cdot d\vec{r}=\int_{C_2}^{ }\vec{F}\cdot d\vec{r}

So, as result, the work done is the same whether we move from A to B through the path C₁ or through the path C₂. Therefore, the path itself does not matter, only the start and end points of the path, which is the definition of path independence.

The calculation we did here was general in the sense that we did not define any particular path or force (besides the fact that it had to be conservative), so this is true for any two paths.

Can Non-Conservative Forces Be Associated With a Potential Energy?

So far, we’ve only discussed how conservative forces can be associated with a potential energy. However, is potential energy only associated with conservative forces?

Potential energy can only be associated with conservative forces. There is no potential energy associated with a non-conservative force, which is due to the fact that non-conservative forces are path dependent. Mathematically, this is a result of Stokes’ theorem for a non-conservative force field.

Let’s first discuss why this is the case in an intuitive sense.

Previously, we deduced that the work done by a gravitational force (an example of a conservative force) is path independent.

On the other hand, consider something like the drag force, which is a force that acts on an object moving through a fluid (such as air) at a relatively slow speed. This force is non-conservative as the work done depends on the path an object moves through the fluid.

The drag force is actually a velocity dependent force, which means that there is a greater force on an object moving at higher speed The direction of the force is always opposite to the velocity of the object:

\vec{f}=-b\vec{v}

This b here is a constant that depends on the properties of the fluid as well as the object itself. Also, throughout this article, I will be denoting non-conservative forces by f instead of F.

The reason I’m bringing this up is because the drag force doesn’t have any particular potential energy associated with it. This is because of the fact that the force is a function of velocity, not position, so we cannot write this force as the gradient of some potential.

However, even forces that do depend on position only are not necessarily conservative. Really, the definition of a non-conservative force is that the work done by that force is path dependent.

Now, recall that for a path dependent (non-conservative) force, the work done around a closed path will generally not be zero (unlike for a conservative force, for which it is always zero):

W=\oint_C\vec{f}\cdot d\vec{r}\ne0

If we now apply Stokes’ theorem, similarly to what we did for conservative forces, we can write this closed line integral as the surface integral of the curl of this force:

\oint_C\vec{f}\cdot d\vec{r}=\int_{ }^{ }\int_S^{ }\left(\vec{\nabla}\times\vec{f}\right)\cdot d\vec{S}\ne0

What this tells us is that the right-hand side is no longer zero like it was for a conservative force, so it also follows that the curl of a non-conservative force is not necessarily always zero:

\vec{\nabla}\times\vec{f}\ne0

On the other hand, recall that if the force could be written as the gradient of potential energy, it would always have zero curl. Therefore, we conclude that a non-conservative force cannot be written in terms of a potential in a sensible or useful way.

Now, you may want to ask; okay, so it cannot be written as the gradient of a potential, but why not just define it in terms of a potential in some other way?

Well, the simple answer is that this defeats the whole purpose of defining a potential energy in the first place; to satisfy energy conservation.

A conservative force is fundamentally written as the negative gradient of potential energy because this is the only way it would conserve the total energy of an object it is acting on (we’ll prove this later in this article).

Therefore, it really doesn’t make any physical sense to define a non-conservative force in terms of a “potential energy”.

Now, sure, you could do this, but it would then only be a mathematical definition and not really a physical “potential energy”.

Interestingly, this IS actually done in Lagrangian mechanics by defining friction forces in terms of the “velocity-gradient” of a dissipation function (which can, in a sense, be thought of as a potential for friction forces).

You can read more about the concept of a dissipation function in this article.

How Do Conservative And Non-Conservative Forces Impact Energy?

The physical effects of both conservative and non-conservative forces are defined in terms of energy conservation and in particular, by how these forces impact the energy of an object.

Conservative forces do not impact the total energy of an object. In other words, total energy is constant if only conservative forces are present. On the other hand, non-conservative forces do not conserve energy, meaning that if non-conservative forces are present, the total energy of an object will change.

Let’s dig a bit deeper into this topic by looking at how each of these forces actually conserve or don’t conserve energy.

A Simple Proof of Energy Conservation

Down below, you’ll find a little proof of the fact that a conservative force does not change the total energy of an object. This proof uses some concepts in vector calculus as well as Newton’s laws.

Proof of Energy Conservation For Conservative Forces

We know that the work done by any force is given by the line integral of the force:

W=\int_C^{ }\vec F\cdot d\vec r

Any force (including non-conservative forces) can be written using Newton’s second law as the time derivative of the momentum of an object that the force is acting on:

\vec F=\frac{d\vec{p}}{dt}

So, the work done by this force can be written as:

W=\int_C^{ }\frac{d\vec{p}}{dt}\cdot d\vec{r}

But, we also know that momentum is mass times velocity (in basic Newtonian mechanics) and velocity is the time derivative of position r, from which we can find another expression for the displacement dr:

\vec{p}=m\vec{v}=m\frac{d\vec{r}}{dt}\ \ \Rightarrow\ \ d\vec r=\frac{\vec{p}}{m}dt

Inserting this into the work integral, we have:

W=\int_C^{ }\frac{d\vec{p}}{dt}\cdot\frac{\vec{p}}{m}dt=\frac{1}{m}\int_C^{ }\vec{p}\cdot d\vec{p}

These dt’s essentially “cancel” here, through this isn’t a very rigorous way of stating it.

Now, this dot product can be written in terms of the magnitudes of these two quantities, p and dp, and the cosine of the angle between the two vectors:

\vec{p}\cdot d\vec{p}=pdp\cos\theta=pdp

Generally speaking, the “change” in momentum always occurs in the same direction of the momentum, or directly opposite to it (this can be deduced directly from Newton’s second law), which means that the angle between these two vectors here is either θ=0 or θ=π, which give either cos(θ)=1 or cos(θ)=-1. Here I’ve chosen the +1 solution.

Using this, the work done in terms of the momentum p is then:

W=\frac{1}{m}\int_C^{ }pdp=\frac{\Delta p^2}{2m}

This line integral of pdp here gives us p²/2 with the integration limits being the start and end points of the path C (a and b). Therefore, when we insert these limits, we simply get p²(b)-p²(a)=Δp², the change in the square of momentum.

Now, if you recognize it, this is nothing but the change in kinetic energy, ΔT (by the relation between momentum and kinetic energy T=p²/2m; I discuss this in great detail in my article on momentum vs kinetic energy). The work done is then just:

W=\Delta T

Now, we can also do the same calculation for a conservative force by using the relation between a conservative force and potential energy:

\vec F=-\vec{\nabla}U

The work done of such a force is then:

W=\int_C^{ }\vec{F}\cdot d\vec{r}=-\int_C^{ }\vec{\nabla}U\cdot d\vec{r}

Here, we can take advantage of something called the gradient theorem, which states that the line integral of the gradient of any function just gives you the value of the function at the start and end points (which for us are a and b):

W=-\int_C^{ }\vec{\nabla}U\cdot d\vec{r}=-\left(U\left(b\right)-U\left(a\right)\right)

The thing inside these parentheses, on the other hand, is nothing but the change in potential energy, ΔU:

W=-\Delta U

We’ve now calculated the work done using two different ways; from the first one, we got W=ΔT and from the second one (which was unique to conservative forces only), we got W=-ΔU. These, of course, have to be equal, so we then get:

\Delta T=-\Delta U\ \ \Rightarrow\ \ \Delta\left(T+U\right)=\Delta E=0

The sum of kinetic energy and potential energy, T+U, is just the total energy E.

So, we get that the change in total energy when a conservative force is acting on an object is exactly zero! Now, the important point about this calculation is that it only works for a conservative force, in which case, conservation of energy just pops out automatically.

Now, the point of the above proof was to show how the assumption of a conservative force automatically leads to energy conservation.

On the other hand, we’ll discuss why the same is not true of a non-conservative force, meaning that a non-conservative force does NOT conserve energy.

Why Is Energy Not Conserved With a Non-Conservative Force?

Energy is not conserved when a non-conservative force acts on an object because some of the kinetic energy of the object will be converted to other forms of energy (such as heat). Mathematically, this is explained by the fact that a non-conservative force cannot be expressed in terms of potential energy.

Really, the fundamental reason for why a non-conservative force does not conserve energy is a purely mathematical result of a force that cannot be written as the gradient of a potential.

The simple way to understand this is to try and repeat the same energy conservation proof we did above, but for a conservative force; you can’t, simply because you cannot define a non-conservative force as the gradient of some potential.

Therefore, we don’t get the general result of ΔE=0, so energy is NOT conserved when a non-conservative force acts on an object (which is also, I suppose, where the name ‘non-conservative force’ comes from).

Now, let’s try to understand why this is the case from an intuitive perspective.

When a non-conservative force acts on an object, the total energy of the object will not stay constant, but rather, energy will be dissipated out of the system (turning energy into heat and other forms of energy, meaning that the object “loses” some energy).

This makes sense if you think about, for example, an object flying through the air. When an object flies through the air, you might intuitively know already that the object begins slowing down and eventually, its motion will stop.

This happens because the object will start experiencing air resistance forces (which are non-conservative velocity-dependent forces) and it will lose energy and therefore also slow down.

It’s also worth noting that energy itself isn’t really “lost” if you account for every possible variable in a system. Energy simply just turns into other forms, such as kinetic energy turning into heat energy.

For example, in the case of an object flying through the air, it might appear that some energy is lost in the process as the object slows down, but that is only if you account for just the object itself.

In reality, if you were to account for truly the whole system, that would include all of the air molecules as well, then any energy wouldn’t be lost.

The energy that appeared to be “lost” would actually just turn into the kinetic energy of the air molecules, which on the larger scale, would appear as heat.

So, actually, the physical distinction between a conservative and a non-conservative force is really just that a force will “appear” as being non-conservative if some part of a given system is not taken into account.

How To Tell If a Force Is Conservative or Non-Conservative (A Simple Method)

We’ve talked a lot about the differences between conservative and non-conservative forces, but how do you actually tell whether a force is conservative or non-conservative? Is there some easy way to check?

To check whether a force is conservative or non-conservative, simply calculate the curl of the force defined in terms of partial derivatives. If the curl of the force is zero, the force is conservative. If on the other hand, the curl of the force is not zero, the force is non-conservative.

We actually already saw the explanation for why this is the case in one of the examples earlier. The mathematical reason for this comes from Stokes’ theorem:

\oint_C\vec{F}\cdot d\vec{r}=\int_{ }^{ }\int_S^{ }\left(\vec{\nabla}\times\vec{F}\right)\cdot d\vec{S}

The details of this are not important (for all the details, consider checking out my Advanced Math For Physics -course), but the left-hand side here is just the work done by the force F over a closed path. If the force is conservative, this has to be zero.

For the left-hand side to be zero, also the right-hand side has to be zero, so we can conclude that for a conservative force, the following condition has to be true:

\vec{\nabla}\times\vec{F}=0

On the other hand, if we have a non-conservative force (f), the work done around a closed path is not necessarily zero and we generally have:

\vec{\nabla}\times\vec{f}\ne0

So, to check whether a force is conservative or non-conservative, just calculate its curl. I like to call this the curl-test.

Usually this will be done using the standard formula for the curl of a vector field in Cartesian coordinates:

\vec{\nabla}\times\vec{F}=\left(\frac{\partial F_z}{\partial y}-\frac{\partial F_y}{\partial z}\right)\hat{x}+\left(\frac{\partial F_x}{\partial z}-\frac{\partial F_z}{\partial x}\right)\hat{y}+\left(\frac{\partial F_y}{\partial x}-\frac{\partial F_x}{\partial y}\right)\hat{z}

The x, y and z with “hats” are the basis vectors in these directions. The curl is therefore a vector, so for it to be zero, ALL of these components have to be zero. These F_x, F_y and F_z are the components of the force.

You’ll find an example of using this down below. Now, this curl-test also works in other coordinate systems, but the formulas for the curl in those coordinate systems are generally more complicated.

Practical Example: Curl-Test For The Gravitational Force

For this example, we’re going to take the gravitational force in two dimensions (in Cartesian coordinates):

\vec{F}\left(x{,}y\right)=-GMm\frac{x}{\left(x^2+y^2\right)^{\frac{3}{2}}}\hat{x}+-GMm\frac{y}{\left(x^2+y^2\right)^{\frac{3}{2}}}\hat{y}

In case you’re wondering where this comes from, we derived this Cartesian form of the gravitational force in one of the earlier examples.

Now, technically, the curl of a vector field is only defined in three dimensions, but I wanted to take this example to illustrate that this curl-test does work in two dimensions also.

All we essentially do is “imagine” that this force has a z-component that is zero:

\vec{F}\left(x{,}y\right)=-GMm\frac{x}{\left(x^2+y^2\right)^{\frac{3}{2}}}\hat{x}+-GMm\frac{y}{\left(x^2+y^2\right)^{\frac{3}{2}}}\hat{y}+0\hat z

So, the components of this force are:

F_x=-GMm\frac{x}{\left(x^2+y^2\right)^{\frac{3}{2}}}{,}\ F_y=-GMm\frac{y}{\left(x^2+y^2\right)^{\frac{3}{2}}}{,}\ F_z=0

To calculate the curl, it’s often easiest to do it component-by-component. Let’s begin with the x-component of the curl:

\left(\vec{\nabla}\times\vec{F}\right)_x=\frac{\partial F_z}{\partial y}-\frac{\partial F_y}{\partial z}=0

You can easily see why this is automatically zero; nothing depends on the z-coordinate and the z-component of the force is zero.

The y-component is, by the same logic, also zero:

\left(\vec{\nabla}\times\vec{F}\right)_y=\frac{\partial F_x}{\partial z}-\frac{\partial F_z}{\partial x}=0

The z-component is the only one, which perhaps has a possibility of being non-zero:

\left(\vec{\nabla}\times\vec{F}\right)_z=\frac{\partial F_y}{\partial x}-\frac{\partial F_x}{\partial y}

Let’s calculate these partial derivatives of the force components:

\frac{\partial F_y}{\partial x}=\frac{\partial}{\partial x}\left(-GMm\frac{y}{\left(x^2+y^2\right)^{\frac{3}{2}}}\right)\\=-GMmy\cdot\left(-\frac{3}{2}\right)\left(x^2+y^2\right)^{-\frac{5}{2}}\cdot2x=GMm\frac{3xy}{\left(x^2+y^2\right)^{\frac{5}{2}}}

\frac{\partial F_x}{\partial y}=\frac{\partial}{\partial y}\left(-GMm\frac{x}{\left(x^2+y^2\right)^{\frac{3}{2}}}\right)\\=-GMmx\cdot\left(-\frac{3}{2}\right)\left(x^2+y^2\right)^{-\frac{5}{2}}\cdot2y=GMm\frac{3xy}{\left(x^2+y^2\right)^{\frac{5}{2}}}

These partial derivatives are, of course, the same, so the z-component of the curl is:

\left(\vec{\nabla}\times\vec{F}\right)_z=\frac{\partial F_y}{\partial x}-\frac{\partial F_x}{\partial y}=GMm\frac{3xy}{\left(x^2+y^2\right)^{\frac{5}{2}}}-GMm\frac{3xy}{\left(x^2+y^2\right)^{\frac{5}{2}}}=0

So, we have that ALL the components of the curl are zero and therefore, the curl itself is also zero:

\vec{\nabla}\times\vec{F}=0

Therefore, the gravitational force is conservative! Now, of course, this result was expected but this example still illustrates the curl-test quite well.

In case you’re interested in some more physics applications of conservative forces, I’d highly recommend reading up on Lagrangian mechanics, which is practically based on the fact that conservative forces can be expressed in terms of potential energy.

I have an entire article on Lagrangian mechanics that introduces the topic in a very beginner-friendly way and also an article comparing Lagrangian mechanics to Newton’s laws.

Examples of Conservative Forces

When we consider specific types of forces and want to know whether some force is conservative or not, it’s worth keeping in mind that the notions of ‘conservative’ and ‘non-conservative’ are, strictly speaking, only defined for forces that can can be described as vector fields.

For example, the tension in a string or the force exerted by a person pushing a box don’t really make sense as vector fields, generally speaking, so we cannot definitely define whether these forces are conservative or non-conservative.

On the other hand, something like friction or air resistance can be seen as vector fields even though these are velocity-dependent forces (simply by considering the velocity of an object as a vector field that has some specific value and direction for the velocity at every point in space).

In any case, you’ll find some examples of forces that are conservative down below. Note that these are all ‘radial’ forces, meaning that they are only functions of r.

You can express them in terms of x, y and z if you wish by using the following relations:

r=\sqrt{x^2+y^2+z^2}

\hat{r}=\frac{1}{r}\left(x\hat{x}+y\hat{y}+z\hat{z}\right)

Gravitational Force

Gravity is a conservative force since the work done by a gravitational field on an object does not depend on the path taken by the object. This is also explained by the fact that the gravitational force can be expressed in terms of the gradient of the gravitational potential.

The gravitational force (between two masses m and M) as a vector field is given by Newton’s law of gravity:

\vec{F}\left(r\right)=-\frac{GMm}{r^2}\hat{r}

The gravitational force can be written as the negative gradient of the gravitational potential energy:

U\left(r\right)=-\frac{GMm}{r}

Electrostatic Force

The electrostatic force, which is the force between two stationary charged particles, is a conservative force since the work done by the electrostatic force is path independent. Because the electrostatic force is conservative, it can be expressed in terms of electric potential energy.

The electrostatic force (between two charges q and Q) is given by Coulomb’s law, which has quite a similar form to Newton’s law of gravity:

\vec{F}\left(r\right)=\frac{qQ}{4\pi\varepsilon_0r^2}\hat{r}

This can be written as the negative gradient of the electric potential energy:

U\left(r\right)=\frac{qQ}{4\pi\varepsilon_0r}

Spring Force

The spring force is a conservative force as the work done in stretching a spring only depends on the displacement of the spring, in other words, only on the end points of the path that the spring is stretched along. Because the spring force is conservative, it can be expressed in terms of potential energy.

If we have a spring that is stretched in some direction (given by the r-unit vector) the spring force, i.e. the restoring force that is opposite to the displacement r, would be given Hooke’s law:

\vec{F}\left(r\right)=-kr\hat{r}

Note; this assumes that the spring constant k is the same for all the x-, y- and z-directions.

This can be written as the negative gradient of the spring potential energy:

U\left(r\right)=\frac{1}{2}kr^2

Examples of Non-Conservative Forces

Below I’ve collected some examples of non-conservative forces as well as explanations of why they’re non-conservative forces.

Friction (Viscosity & Drag)

The force of friction can come in many different forms, but generally friction is thought of as a velocity-dependent force. But how exactly does this make friction a non-conservative force?

Friction is a non-conservative force as the work done by friction on an object depends on the specific path that the object moves along. This is because friction is a velocity-dependent force, meaning that the energy lost from friction depends on the velocity of an object at each point along its path.

One way to model a velocity-dependent friction force is as a linear function of velocity:

\vec{f}\left(t\right)=-b\vec{v}\left(t\right)

The b here is simply a proportionality constant.

The time dependence here comes from the fact that velocity is a function of time, generally speaking. Now, the work done by such a friction force would be:

W=\int_C^{ }\vec{f}\left(t\right)\cdot d\vec{r}=-b\int_C^{ }\vec{v}\left(t\right)\cdot d\vec{r}

We can write this as (by using the fact that v(t)=dr/dt, which means that dr=v(t)dt):

W=-b\int_C^{ }\vec{v}\left(t\right)\cdot d\vec{r}=-b\int_C^{ }\vec{v}\left(t\right)\cdot\vec{v}\left(t\right)dt=-b\int_C^{ }v^2\left(t\right)dt

The noteworthy thing about this is that, unlike the work done by a conservative force, this depends on the path the object moves along (C). In contrast, the work done by a conservative force is simply the potential energy difference between the end points of the path.

Now, this linear velocity-dependent friction is often used to model the viscous force acting on an object that is moving through a fluid at relatively low speed.

For a faster moving object, the friction would be modeled by the drag force, which is a quadratic function of velocity:

\vec{f}\left(v\right)=-\frac{1}{2}bv^2\hat v

This v-hat here is a unit vector in the direction of the velocity.

The work done by such a force would be:

W=\int_C^{ }\vec{f}\left(t\right)\cdot d\vec{r}=-\frac{1}{2}b\int_C^{ }v^2\left(t\right)\hat{v}\cdot\vec{v}\left(t\right)dt=-\frac{1}{2}b\int_C^{ }v^3\left(t\right)dt

We can, once again, see that this depends on the path taken.

Induced Electromotive Force

The electromotive force (which is actually a voltage difference, not a force in the usual sense of the word) is the effect produced by a changing magnetic field that induces an electric field around a closed loop.

The induced electric field that a changing magnetic field (i.e. a magnetic field that is a function of time) produces is non-conservative in nature. In other words, the work done by such an electric field is path dependent and the electric field cannot be expressed in terms of an electric potential.

We can understand why an induced electric field is non-conservative by using Stokes’ theorem for an electric field:

\oint_C^{ }\vec{E}\cdot d\vec{r}=\int_{ }^{ }\int_S^{ }\left(\vec{\nabla}\times\vec{E}\right)\cdot d\vec{S}

Normally, the right-hand side here would be zero (as is the case for an electrostatic force) and the electric field would be conservative.

However, if there happens to be a time-varying magnetic field, then by the Maxwell-Faraday equation, the curl of the electric field will NOT be zero. Instead, it will be proportional to the time derivative of the magnetic field:

\vec{\nabla}\times\vec{E}=-\frac{\partial \vec B}{\partial t}

Stokes’ theorem then becomes:

\oint_C^{ }\vec{E}\cdot d\vec{r}=-\int_{ }^{ }\int_S^{ }\frac{\partial\vec{B}}{\partial t}\cdot d\vec{S}

Now, the left-hand side here is the work done by the electric field around a closed path and as we can see from this, in the presence of a time-varying magnetic field, it is no longer zero.

Therefore, this electric field produced by a varying magnetic field is non-conservative and so is the electric force produced by this induced electric field.

In fact, the thing on the right-hand side is usually taken as the definition of the electromotive force (which isn’t really a force, per say, but rather a voltage as it has units of volts).