Are Maxwell’s Equations Relativistic? (Simple Explanation & Proof)

Electromagnetism is one of the cornerstones of modern physics, taking its place next to special and general relativity. It is only natural, then, to ask how compatible these two theories are. Are Maxwell’s equations truly relativistic?

Maxwell’s equations are fully relativistic, which follows from the fact that they are covariant under Lorentz transformations and preserve the speed of light. Maxwell’s equations are, however, only compatible with special relativity and not with Galilean relativity.

In this article, we cover what it means for an equation to be relativistic (i.e. compatible with special relativity). We will look at Lorentz transformations and see that Maxwell’s equations are covariant under them.

We’ll also discuss the problem of Galilean relativity, how this relates to Maxwell’s equations and why Einstein was motivated to develop his special theory of relativity based on the properties of Maxwell’s equations.

If you’re new to special relativity, I’d recommend reading this introduction to special relativity. However, this isn’t absolutely necessary in order to understand what we’re going to discuss in this article.

You may also like my Advanced Math For Physics -course, if advanced electrodynamics and the math behind it is something you’re interesting in learning more deeply.

Why Maxwell’s Equations Are Relativistic

I want to first present an intuitive explanation for why Maxwell’s equations are relativistic before we look at this mathematically. To understand this, however, we need to first discuss Lorentz transformations.

Fundamentally, relativity has its roots in the following two statements:

• The laws of the universe should look the same to all observers.
• All observers should agree on the speed of light.

If we have an equation that preserve these two conditions, then we say that the equation is relativistic.

However, we first have to agree on what counts as an “observer.” An observer is one whose frame of reference is inertial: it is not accelerating. An observer in an inertial frame is therefore moving at constant velocity.

These inertial reference frames have the wonderful property that Newton’s first law (an object in motion continues in motion unless acted on by a force) must hold, since we are not introducing any extra “forces” or accelerations in the observer’s frame.

Now, a reference frame is simply just a description of an observer’s state of motion – it describes how the observer would measure time and space. We typically describe this by assigning a coordinate system (with both spatial and time axes) to the observer.

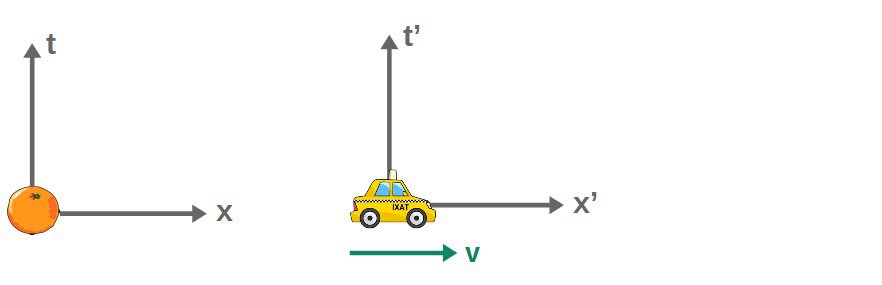
The important thing for us is how the reference frames of different observers are compared. We essentially compare reference frames by doing a transformation from one frame to another.

We can characterize these transformations generally as translations, rotations, and boosts.

To visualize a translation, imagine two people stood on a long ruler in the same place. If one person moves along the ruler, they have undergone a translation.

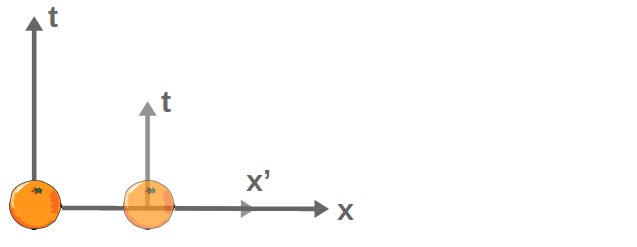
Visualizing a rotation isn’t much harder. Imagine two people on a merry-go-round (or carousel) who are stood at the edge and looking at the center.

These two observers are related by a rotation about the center – the distance from the center doesn’t change, just the angle between them!

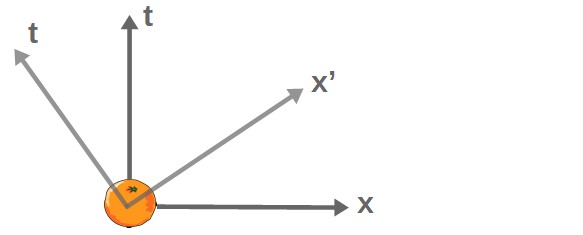
The boosts are what we’re specifically interested in. In special relativity, these boosts from one frame to another are called Lorentz transformations. These are the key to understanding why Maxwell’s equations are relativistic.

Now, a (Lorentz) boost is a bit harder to visualize. Essentially, these boosts are transformations between reference frames that are moving with different (constant) velocities.

So, to (relativistically) transform from the frame of an observer moving at 5 m/s in some direction to the frame of an observer moving at 14 m/s in some other direction would require a Lorentz boost.

You can boost in any direction, however, generally, a Lorentz transformation will also consist of some kind of rotation. For simplicity, let’s try and imagine a boost in the x-direction.

If one observer is at rest, then a boosted observer’s frame of reference is moving in the x-direction with relative velocity v.

What is special about the Lorentz boost is that it mixes the time and space coordinates of the two observers – meaning that Lorentz transformations actually act on spacetime itself!

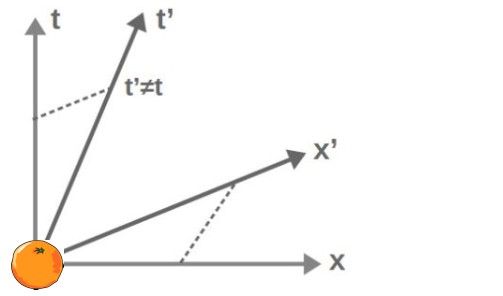
In fact, this property of the Lorentz boosts is the reason behind all the weird phenomena of special relativity (time dilation, length contraction and so on).

This family of translations, rotations, and boosts is known as the family of Poincaré transformations. If we ignore translations, we get the family of Lorentz transformations.

This is the heuristic perspective – we can formalize this a bit further with some math, which we’ll do soon. But first, how does all of this relate to Maxwell’s equations?

Maxwell’s Equations & Lorentz Transformations

When we say an equation is relativistic, all we mean is that the equation has the same form in all reference frames.

So, an equation being relativistic means that the equation preserves its form when we transform it from one reference frame to another through a Lorentz transformation. Lorentz transformations therefore determine whether something is compatible with special relativity or not.

The special thing about Lorentz transformations is that they preserve the speed of light – this is why according to special relativity, the speed of light is the same for all observers.

Now, the important thing for us is that it turns out Maxwell’s equations also preserve their form under Lorentz transformations. We describe this by saying that Maxwell’s equations are Lorentz covariant.

This means that according to special relativity, Maxwell’s equations remain the same for all observers and thus, they are fully relativistic.

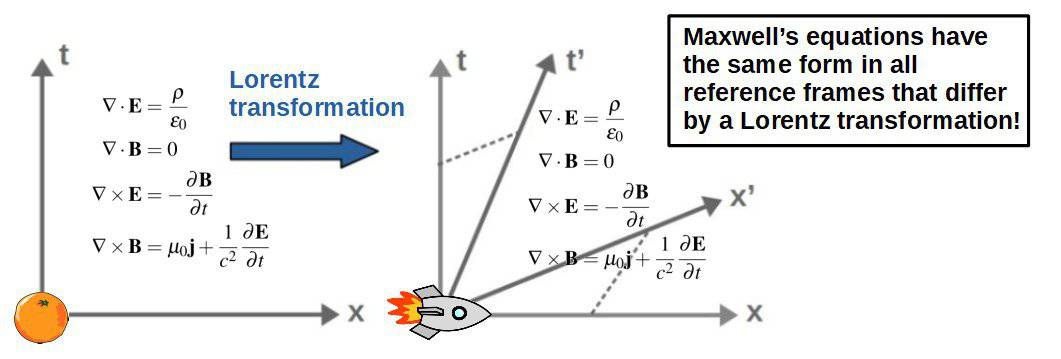
This is the fundamental reason why we say that Maxwell’s equations are relativistic or compatible with special relativity – they remain the same for all relativistic observers!

Before we look at how this comes about mathematically, it’s important to understand why Maxwell’s equations have this Lorentz covariance property.

The simple answer is because we define Lorentz transformations as transformations that preserve Maxwell’s equations in the first place – this is the real reason why special relativity and Lorentz transformations were originally invented.

Because of this historical artefact, Maxwell’s equations being the basis of Einstein’s special relativity as we know it meant that they were always going to be relativistic in the first place! Relativity itself was built to be something that makes Maxwell’s equations relativistic, as weird as that may sound.

Maxwell’s Equations & Galilean Relativity

Before relativity à la Einstein, there was Galilean relativity.

Galilean relativity is what determines transformations between reference frames that are compatible with Newton’s laws (but not with special relativity).

Here, I want to briefly discuss how Maxwell’s equations behave under Galilean relativity. As it turns out, Maxwell’s equations are NOT compatible with Galilean relativity and therefore, not compatible with Newton’s laws either.

It’s important to understand this, because this is one of the main reasons why special relativity was invented in the first place.

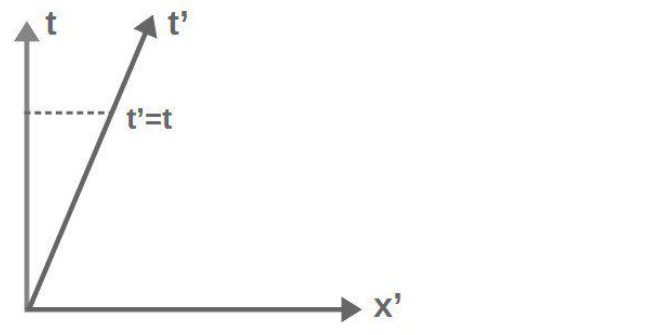
In Galilean relativity, the transformations between reference frames consist of translations, rotations, and boosts. The translations and rotations are very much the same as in Einstein’s special relativity, however the boosts look different.

The main difference is that a Galilean boost does NOT change the time coordinates of an observer in any way – time is a universal quantity in Galilean relativity.

Mathematically, we can represent Galilean boost in, say the x-direction, in the form:

x'=x-vt

This tells us that the observers are moving at a speed v relative to each other. If we divide by time, we get an equation telling us about the relative velocities:

V'=V-v

This innocent-looking equation is the root of the main problem of Galilean relativity.

To illustrate this, imagine a person on a train. The train is travelling at speed v. There is a second person stood at a train station who intends on looking inside the train.

The person on the train then emits some light straight forward at the speed of light, c. The person at the train station witnesses this and according to them (based on a Galilean boost), the light would be travelling at speed v+c.

This would be greater than the speed of light, which cannot be true according to special relativity and everything we know about physics!

We know that photons mediate the electric and magnetic field and travel at the speed of light. This is, in fact, manifest in Maxwell’s equations.

Maxwell’s equations are not invariant under Galilean transformations for the same reason as the speed of light is not.

Now, the point of discussing this is to highlight an important point – Maxwell’s equations are only compatible with one group of transformations, the Lorentz transformations.

In fact, if we want Maxwell’s equations to be valid for all observers, then we have to demand that Lorentz transformations are the valid transformations between frames, not Galilean transformations. For the rest of this article, we will therefore assume special relativity to be true.

What Makes An Equation Relativistic?

When we say that an equation is relativistic, we simply mean that the equation is compatible with special relativity.

An equation is said to be relativistic if it has the same form for all observers and in all reference frames. Mathematically, this means that an equation is relativistic if the equation preserves its form when transforming it from one reference frame to another by a Lorentz transformation.

Next, we’re going to dive deeper into the math behind what actually makes an equation relativistic and then apply the math we learn to see that Maxwell’s equations indeed are relativistic.

As mentioned before, each observer moving at some velocity relative to another observer has their own reference frame. This reference frame can be quantitatively described by a set of coordinates.

In special relativity, we’re always dealing with both time and space, so generally, each observer will have four coordinates – one temporal and three spatial.

In relativity, we label the coordinates of an observer by a four-component object denoted as x^μ, where the index μ can take on values 0, 1, 2 or 3 (with μ=0 describing the temporal part and μ=1,2,3 describing the spatial coordinates).

We can imagine this as a column vector:

x^{\mu}=\begin{pmatrix}ct\\x\\y\\z\end{pmatrix}

Here, c is the speed of light and is necessary to be there so that each component has the dimension of length (Recall distance = speed times time). So, c here is just a constant that works as a conversion factor.

If we drop the superscript μ for a moment and treat x^μ as a column vector, we can describe the family of Poincaré transformations from x to x’ as (x’ being just a set of different coordinates, the coordinates of another observer):

x'=\Lambda x+b

Here, b represents the translations (including translations in time too) and the matrix Λ encompasses the rotations and boosts.

Let’s consider the rotations next. In particular, let’s rotate around the x-axis first. This is when b=0 and Λ takes the form:

\Lambda=\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&\cos\theta&-\sin\theta\\0&0&\sin\theta&\cos\theta\end{pmatrix}

This looks complicated at first, however, the first two rows just mean “do nothing to the time component or x-component”. The bottom right hand corner can be read as “rotate by angle θ” in the yz-plane.

In general, a rotation is described by a 3×3 matrix R that obeys the rule RR^T= I, where I is the 3×3 identity matrix.

R^T is the “matrix transpose” – the rule is you do nothing along the diagonal but swap opposite entries along the diagonal, so if we take a matrix R:

R=\begin{pmatrix}R_{xx}&R_{xy}&R_{xz}\\R_{yx}&R_{yy}&R_{yz}\\R_{zx}&R_{zy}&R_{zz}\end{pmatrix}

Then, its transpose is given by:

R^T=\begin{pmatrix}R_{xx}&R_{yx}&R_{zx}\\R_{xy}&R_{yy}&R_{zy}\\R_{xz}&R_{yz}&R_{zz}\end{pmatrix}

Altogether, we can describe any rotation as:

\Lambda=\begin{pmatrix}1&\vec{0}\\\vec{0}&R\end{pmatrix}

Now we move on to boosts along the x-axis, which is a mixture between time and space. This is again a Lorentz transformation and is given by the case where b=0 and Λ is given by:

\Lambda=\begin{pmatrix}\cosh\psi&-\sinh\psi&0&0\\-\sinh\psi&\cosh\psi&0&0\\0&0&1&0\\0&0&0&1\end{pmatrix}

This time, the bottom right hand entries represent “do nothing to the y and z coordinates” and the top left tell us to mix the time and x-spatial components!

Boosts are what allow us to keep the second condition – the speed of light is the same in all reference frames.

Rotations and translations won’t change any perceived speeds but a boost changes an observer into a moving frame of reference. However, a Lorentz boost always has the special property of preserving the speed of light.

Let’s consider a boost along the x-direction where we transform from some frame to to the rest frame of an observer (not moving) at the origin. This means that the coordinates in the rest frame, x’, are described in terms of the original coordinates, x, by the equation:

x'=\Lambda x

More explicitly, this says:

\begin{pmatrix}ct'\\0\\0\\0\end{pmatrix}=\begin{pmatrix}\cosh(\psi) ct\sinh(\psi) x\\-\sinh(\psi)ct+\cosh(\psi)x\\y\\z\end{pmatrix}

If we look at the new x’-coordinate, this tells us that x=tanh(ψ)ct. This describes an observer moving at velocity v=tanh(ψ)c.

However, -1<tanh(ψ)<1, therefore this boosted velocity is moving at a speed that is less than the speed of light!

Now we’ve seen how two different observers’ space and time coordinates change under Lorentz transformations, but this is not yet enough to see how Maxwell’s equations transform.

For that, we also need to know how fields (such as the electric field) transform. A field is simply some continuous quantity that has a particular value at each point in space and time – it is a function of the coordinates.

To do this, we’ll introduce the superscript greek letters again.

A scalar field φ(x) transforms very simply, φ(x)=φ'(x’) – it looks exactly the same in all frames! A vector field, however, transforms by the equation:

A'^{\mu}\left(x'\right)=\Lambda_{\nu}^{\mu}A^{\nu}\left(x\right)

In this, we have introduced the “summation convention” – this means that if there is a repeated index in the upper and lower positions, we sum over that index (in our case, we would sum over ν from 0 to 3).

This summation generalizes matrix multiplication. Similarly, something with two upper indices (which is called a tensor field and is often expressed as a matrix) transforms as:

F'^{\mu\nu}\left(x'\right)=\Lambda_{\rho}^{\mu}\Lambda_{\sigma}^{\nu}F^{\rho\sigma}\left(x\right)

If we don’t want to include the indices, we could write this purely in terms of matrices as F’ = ΛFΛ^T.

Finally, if something has a lower subscript such as a derivative, it transforms in the following way:

\partial'_{\mu}=\Lambda_{\mu}^{\nu}\partial_{\nu}

If a scalar field, vector field, derivative etc. follows these transformation rules under a Lorentz transformation, we say that it is Lorentz covariant. By using these covariant objects, we can build up theories governed by relativistic equations, in other words, theories fully compatible with relativity.

This then answers the question of what it means for an equation to be relativistic – if we have an equation that transforms according to the rules given above under a Lorentz transformation and preserves its form, the equation is relativistic!

If the equation doesn’t have the same form after the Lorentz transformation, the equation is not relativistic.

How To Prove That Maxwell’s Equations Are Relativistic

We have now covered what it means for equations to be relativistic mathematically. Next, let’s apply what we’ve learnt to Maxwell’s equations and see if they are indeed relativistic.

Maxwell’s theory of electromagnetism is governed by four equations:

\nabla\cdot\vec{E}=\frac{\rho}{\varepsilon_0}\\\nabla\cdot\vec{B}=0\\\nabla\times\vec{E}=-\frac{\partial\vec{B}}{\partial t}\\\nabla\times\vec{B}=\mu_0\left(\vec{J}+\varepsilon_0\frac{\partial\vec{E}}{\partial t}\right)

Where E and B are the electric and magnetic fields respectively, ρ is the charge density, J is the current density and μ₀ and ε₀ are two constants of nature relating to the electric and magnetic fields in a vacuum.

We can use some mathematical trickery to rewrite these equations in a slightly different way.

The Covariant Form of Maxwell’s Equations

Our goal here is to write the four Maxwell equations in terms of quantities with free indices, so that we can easily apply the Lorentz transformation rules discussed previously. This will lead us to something called the covariant form of Maxwell’s equations.

Now, the second Maxwell’s equation tells us that magnetic fields B cannot come from a point, that there are no “magnetic monopoles:” you cannot cut a magnet in half and find just a North or a South pole on its own.

Mathematically, we can always satisfy this equation by introducing a new field A called the vector potential and define:

\vec{B}=\nabla\times\vec{A}

This holds because “the divergence of the curl is always zero”, one of the key results of vector calculus.

We can then introduce a second field, called the scalar potential, to define the electric field as:

\vec{E}=-\nabla\phi-\frac{\partial \vec{A}}{\partial t}

With these two defined, we can bundle up Maxwell’s equations in a nice form by writing them in terms of two vectors with indices, A^μ and J^μ with components:

A^{\mu}=\left(\frac{1}{c}\phi,\vec{A}\right)\\J^{\mu}=\left(c\rho{,}\vec{J}\right)

With the final ingredient being the Faraday tensor or the electromagnetic field tensor:

F^{\mu\nu}=\partial^\mu A^\nu-\partial^\nu A^\mu

In case you’re interested, I discuss the meaning of this electromagnetic field tensor more in this article. In the article, we use this field tensor to explain why only moving charges create a magnetic field.

It might seem like we are reinventing the wheel here by introducing new objects to describe what we already know, however writing them in terms of this framework makes life easier overall!

Within this new framework, without getting into the details, Maxwell’s equations can be compactly rewritten as:

\partial_{\mu}F^{\mu\nu}=\mu_0J^\nu\\\partial^\sigma F^{\mu\nu}+\partial^{\mu}F^{\nu\sigma}+\partial^\nu F^{\sigma\mu}=0

These are the Lorentz covariant forms of Maxwell’s equations and the nice thing is that the original four Maxwell’s equations can be nicely written as only two equations.

Now, if we were to write out these equations component by component, we’d recover exactly the four original Maxwell’s equations in terms of the electric and magnetic fields.

Therefore, this covariant form is exactly equivalent to the original form of Maxwell’s equations, just expressed in terms of different quantities.

We can see that the first equation has one free index ν, whereas the second has three free indices. The useful thing about this is that we can now easily apply Lorentz transformations to these equations since we know how all of these objects with indices transform (as discussed earlier).

So, let’s see how these equations transform next!

Lorentz Transformation of Maxwell’s Equations

We’ll begin by transforming the first covariant Maxwell’s equation.

What we find after performing a Lorentz transformation from one reference frame to another, arbitrary frame is that the first Maxwell equation remains of exactly the same form:

\partial'_{\mu}F'^{\mu\nu}=\mu_0J^{'\nu}\ \Leftrightarrow\ \ \partial_{\mu}F^{\mu\nu}=\mu_0J^{\nu}

Therefore, this first Maxwell equation is indeed fully relativistic! You’ll find the full proof of this below.

Lorentz Transformation of The First Maxwell's Equation

There is also another way to see that the first Maxwell’s equation is relativistic. This can be done by a so-called action principle and the property that scalars are always invariant (they remain exactly the same) under Lorentz transformations.

To do this, we need to note one thing first – the vector and scalar potentials do not uniquely define Maxwell’s equations.

In fact, there is some freedom called gauge freedom that allows us to change, for example, A by adding on the gradient of a scalar field:

\vec{A}\mapsto\vec{A}+\nabla\psi

This holds due to the second important vector calculus rule: “the curl of the gradient is always zero.”

To limit this freedom and get something closer to a unique solution, we often make a choice of gauge. One of the most common is the Lorenz gauge (not Lorentz), defined in our nice index notation as:

\partial_{\mu}A^{\mu}=0

Using this gauge, we can rewrite (one final time) the first Maxwell equation as:

\mu_0J^\nu=\partial_\mu F^{\mu\nu}=\partial_\mu \left(\partial^\mu A^\nu-\partial^\nu A^\mu\right)\\=\partial^2 A^\nu-\partial_\mu\partial^\nu A^\mu=\partial^2 A^\nu-\partial^\nu\partial_\mu A^\mu=\partial^2 A^\nu

Here, I’ve simply inserted the definition of the Faraday tensor from earlier. Also, since the combination ∂_µ∂^µ contains a sum over the index µ, this term does not actually have any free indices and is therefore just a scalar (here labeled as ∂², however, this doesn’t literally mean “∂ squared” – it’s just notation).

It turns out that we can derive this equation from a scalar quantity and the nice thing is that a scalar is always the same for all observers – hence we know that this Maxwell’s equation must already be relativistic! You’ll find how this is done below.

Maxwell's Equations from an Action Principle

So far, we’ve seen that one of our Maxwell’s equations is relativistic. Let’s now show that our second equation looks the same for any observer, in other words, is also relativistic.

The second equation is made of building blocks that look like ∂^σF^μν, which transform as:

\partial'^{\sigma}F'^{\mu\nu}\ \ \Rightarrow\ \ \Lambda_{\rho}^{\sigma}\partial^{\rho}\left(\Lambda_{\alpha}^{\mu}\Lambda_{\beta}^{\nu}F^{\alpha\beta}\right)=\Lambda_{\alpha}^{\mu}\Lambda_{\beta}^{\nu}\Lambda_{\rho}^{\sigma}\partial^{\rho}F^{\alpha\beta}

Since each part of the equation has the same indices and thus, each term will contain the same Lorentz matrices, the transformed equation becomes:

\partial'^{\sigma}F'^{\mu\nu}+\partial'^{\mu}F'^{\nu\sigma}+\partial'^{\nu}F'^{\sigma\mu}=0 \Rightarrow\ \ \Lambda_{\rho}^{\sigma}\Lambda_{\alpha}^{\mu}\Lambda_{\beta}^{\nu}\left(\partial^{\rho}F^{\alpha\beta}+\partial^{\alpha}F^{\beta\rho}+\partial^{\beta}F^{\rho\alpha}\right)=0

However, this can only be true generally if the part in the brackets itself is zero, so:

\partial^{\rho}F^{\alpha\beta}+\partial^{\alpha}F^{\beta\rho}+\partial^{\beta}F^{\rho\alpha}=0

This is just the second Maxwell’s equation we had before but with different index letters! However, it has exactly the same form as the original one, so indeed, this equation is also compatible with Lorentz transformations and thus, relativistic.

We’ve now verified that both of the covariant forms of Maxwell’s equations are indeed fully relativistic.

Therefore, equivalently the original four Maxwell’s equations (written in terms of the electric and magnetic fields) must also be fully relativistic. It’s just more cumbersome to verify that by using the “standard” forms of Maxwell’s equations, which is why we reverted to using the covariant index form here!