The Metric Tensor: A Complete Guide With Examples

If you’ve looked into general relativity or differential geometry, you might have come across the metric tensor at some point. It is one of the most fundamental tools used in the study of curvature, among many other things.

In short, the metric tensor is a mathematical object that describes the geometry of a coordinate system or manifold. The components of the metric describe lengths and angles between basis vectors. In general relativity, these components are solutions to the Einstein field equations.

In this article, we will be going over everything you need to know about the metric tensor, along with its geometric meaning and applications in physics.

We will also look at plenty of practical examples along the way. This allows you to see how the metric tensor is actually used – perhaps you’ll be able to do calculations with it yourself after this article!

Why Do We Need The Metric Tensor?

Let’s begin by discussing why we even care about the metric tensor in the first place.

The most common applications of the metric tensor can be found in Riemannian geometry. It also has lots of applications in physics and tensor calculus, to name a few.

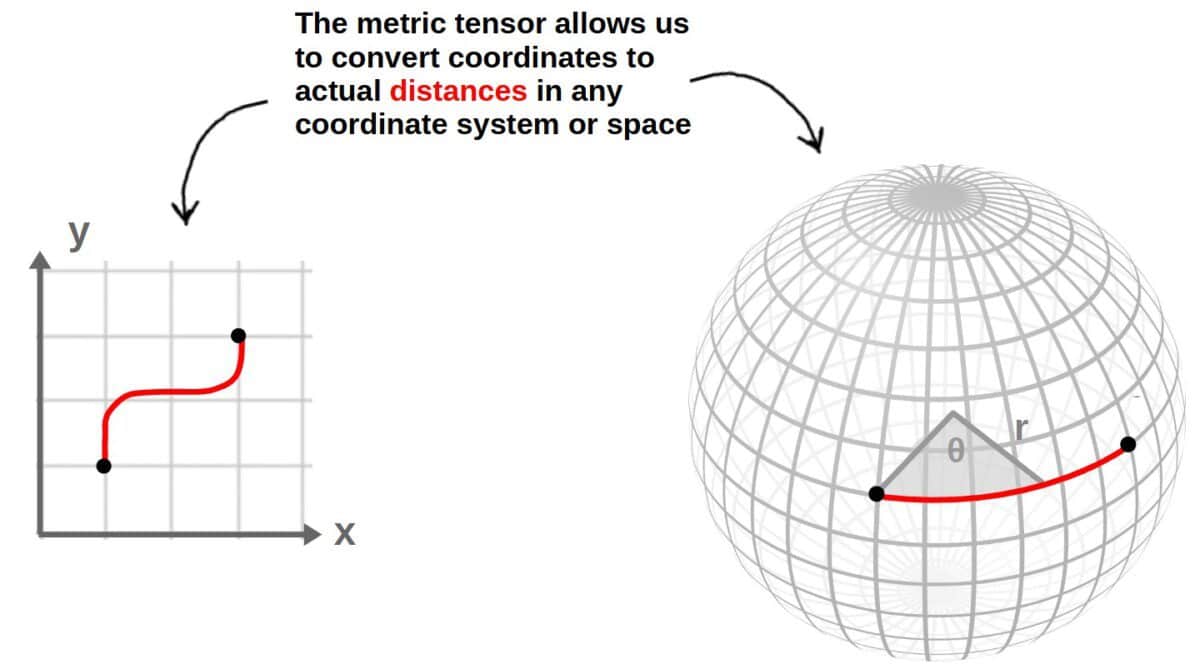
Perhaps the most important job of the metric – in practice – is to convert coordinates to distances.

Therefore, we need the metric whenever we want to analyze the geometry of a given coordinate system or space. In particular, if we want to define a notion of distance, the metric tensor is the fundamental tool for doing so.

Apart from defining distances even in curved spaces, the metric tensor has plenty of other applications as well:

• The metric defines the dot product for any space. Therefore, it is needed if we want to calculate norms of vectors or any kind of angles.
• The metric allows us to describe spacetime curvature in general relativity and therefore, gravity. In fact, the metric tensor can be thought of as playing the role of a gravitational potential in general relativity.
• The metric is used in practically any calculation involving tensors and index notation. This is because it allows us to raise and lower indices of tensor components.

These are just a few of the most important applications of the metric tensor. After this article, the goal is that you’ll be able to understand all of them – and much more!

Geometric Interpretation of The Metric Tensor

The metric tensor defines the geometry of different coordinate systems and spaces. It describes lengths, angles and other geometric quantities. Next, we will look at how it does this.

In short, the metric tensor stores information about lengths, angles, areas and volumes in a given coordinate system or manifold. The components of the metric determine how distances are calculated from coordinates, while its determinant describes areas and volumes.

The way the metric tensor describes all of this is by defining a dot product for the given coordinate system or manifold. The dot product then allows us to calculate things like distances and angles. In the following sections, we’ll look at all of this.

Components of The Metric

The metric is a tensor and like vectors, tensors generally have components in any particular coordinate system we are using. These components are used to represent the tensor itself in that coordinate system.

The components of the metric tensor are defined as the dot product between basis vectors:

g_{ij}=\vec{e}_i\cdot\vec{e}_j

Here, g_ij are the components of the metric tensor and these e’s are the basis vectors in whatever coordinate system we are using. The indices i=1,2,3,… and j=1,2,3,… label which basis vectors or components we are referring to.

It’s quite common to collect these components into a matrix, with the index i running over the rows and j running over the columns:

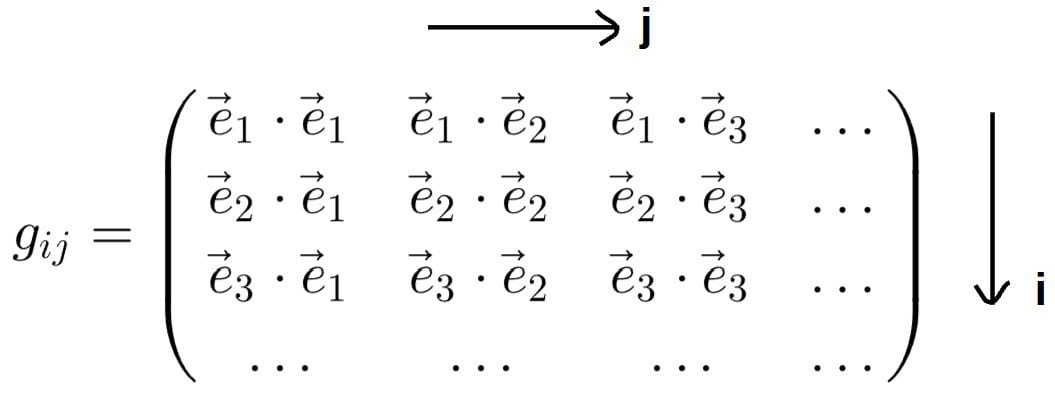
Now, why such a definition? Well, the dot product between basis vectors is enough to describe the geometry of any given coordinate system.

Let’s think about why this is. Fundamentally, any coordinate system can be completely described by constructing a basis for it (at each point, in the general case) – that is, specifying a set of basis vectors at each point.

The dot product between the basis vectors then determines the relative direction and length of each one, which is enough to determine pretty much the entire coordinate system itself – we know which direction the basis vectors point to, and their lengths.

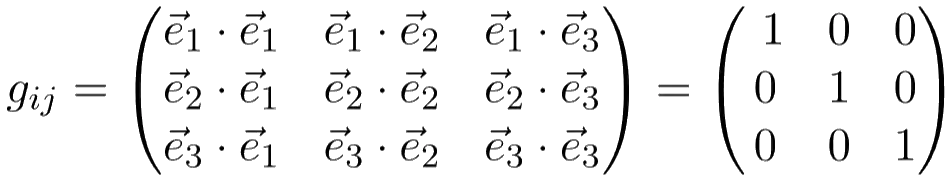
Let’s look at the metric components in a bit more detail:

• The diagonal components (with i=j) describe the length squared of each basis vector, because each one consists of the dot product of a given basis vector by itself.
• The off-diagonal elements (with i≠j) describe the overlap of a given basis vector with another one. Thus, they determine the angles between each basis vector. For orthogonal coordinate systems, these components are always zero, so the metric is diagonal.

So, say we have some arbitrary coordinate system with coordinate axes x¹ and x² and basis vectors in the corresponding directions. The metric (at each point) would then describe the lengths of both basis vectors and the alignment of the basis vectors:

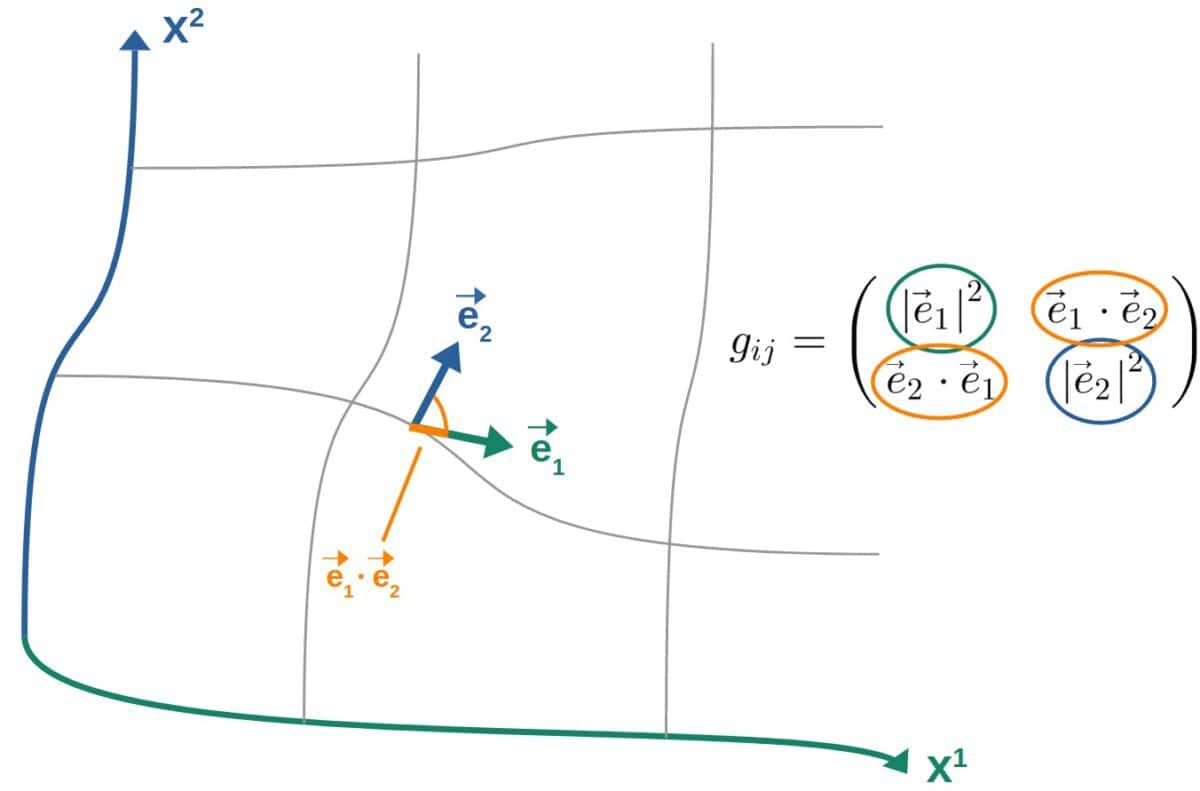
Now, because the metric tensor defines the dot product between basis vectors, it also defines the dot product between any other pair of vectors. This comes from the fact that we can always write two vectors in a basis as linear combinations of the vector components and the basis vectors:

\vec{v}=v^i\vec{e}_i \vec{u}=u^j\vec{e}_j

We are using the so-called Einstein summation convention here, meaning that any repeated index occurring in both the downstairs and upstairs positions in the same term is to be summed over. Thus, both i and j here are summation indices.

The dot product between these is then:

\vec{v}\cdot\vec{u}=\left(v^i\vec{e}_i\right)\cdot\left(u^j\vec{e}_j\right)=v^iu^j\vec{e}_i\cdot\vec{e}_j=v^iu^jg_{ij}

Therefore, the metric essentially determines how the dot product between any two vectors is calculated in a given coordinate system. This is why we often say the metric defines a dot product.

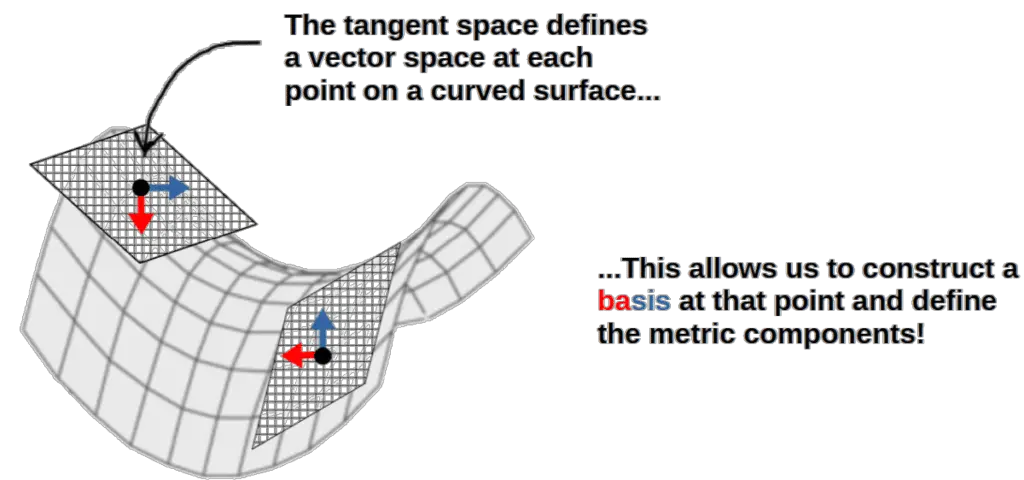
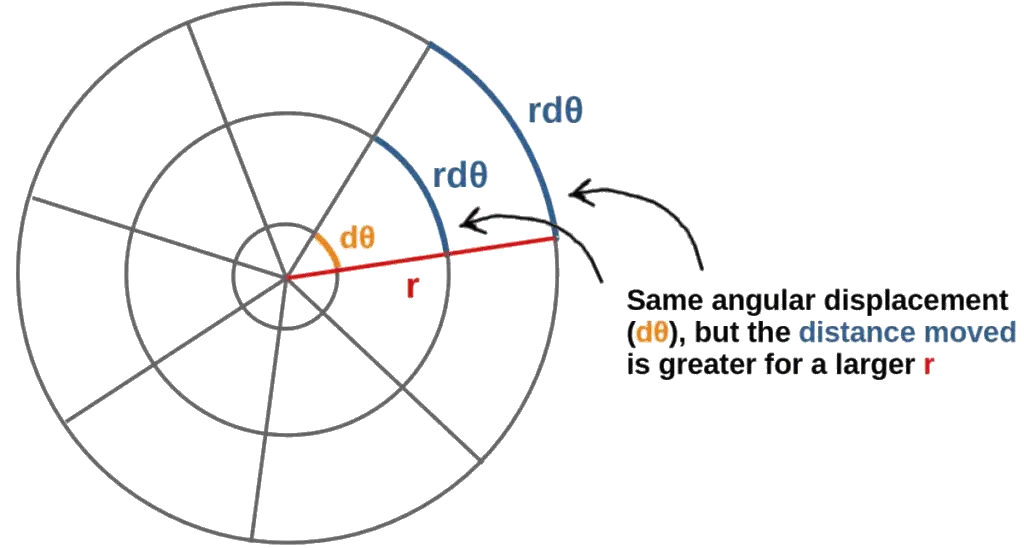
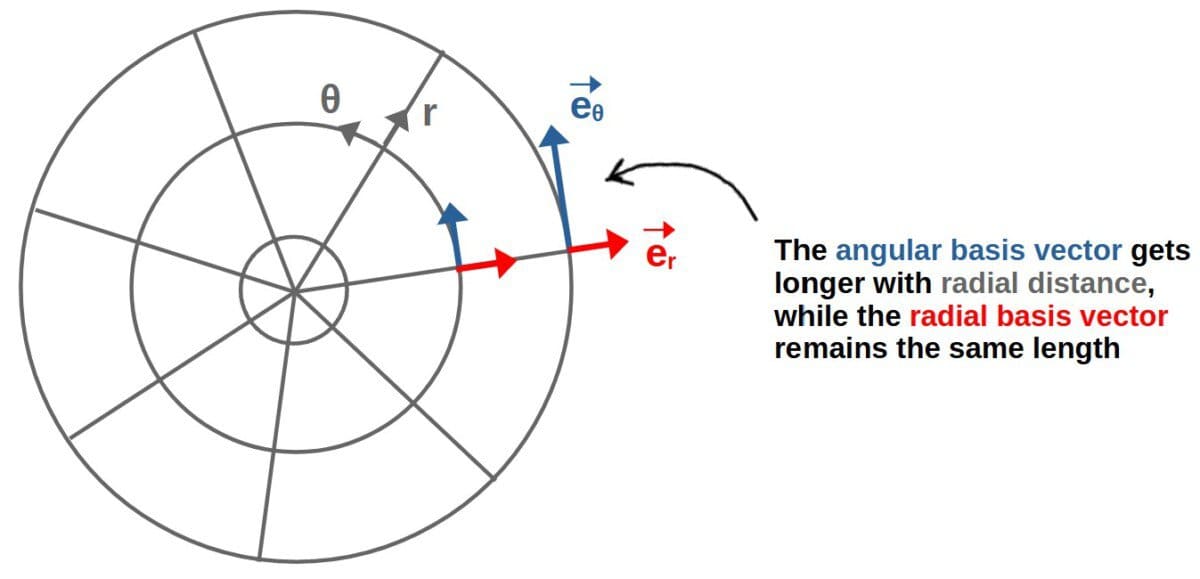
As an illustrative example of what the metric tensor components actually tell us, let’s look at the polar coordinate system. This consists of a radial coordinate r and an angular coordinate θ, with basis vectors in the corresponding directions.

The metric components have the following form in polar coordinates:

g_{ij}=\begin{pmatrix}1&0\\0&r^2\end{pmatrix}

These, and many more metrics, are derived in detail in my Mathematics of General Relativity -course. Just a heads up, in case you want to understand more of the practical details behind everything!

First of all, the off-diagonal elements being zero here tells us that the polar basis vectors are orthogonal, since the dot products between them is zero. Moreover, the radial basis vector has a constant length of 1 everywhere (like the Cartesian basis vectors).

The more interesting part is the metric component g₂₂=g_θθ=r², which tells us that the length squared of the θ-basis vector is r². Therefore, the angular basis vector actually gets longer with radial distance to the origin:

Scale Factors

One of the important features of the metric tensor is for describing lengths in arbitrary coordinate systems or manifolds. We already saw a few examples of this previously with the diagonal the metric components describing the lengths of basis vectors.

Generally, the square roots of the diagonal components of the metric tensor are called scale factors and they describe the length of each basis vector in a given coordinate system. Scale factors are commonly used in vector calculus, for example, for calculating gradients in curvilinear coordinates.

We usually label the scale factors as h_i, where the index i denotes which of the diagonal components of the metric we are referring to:

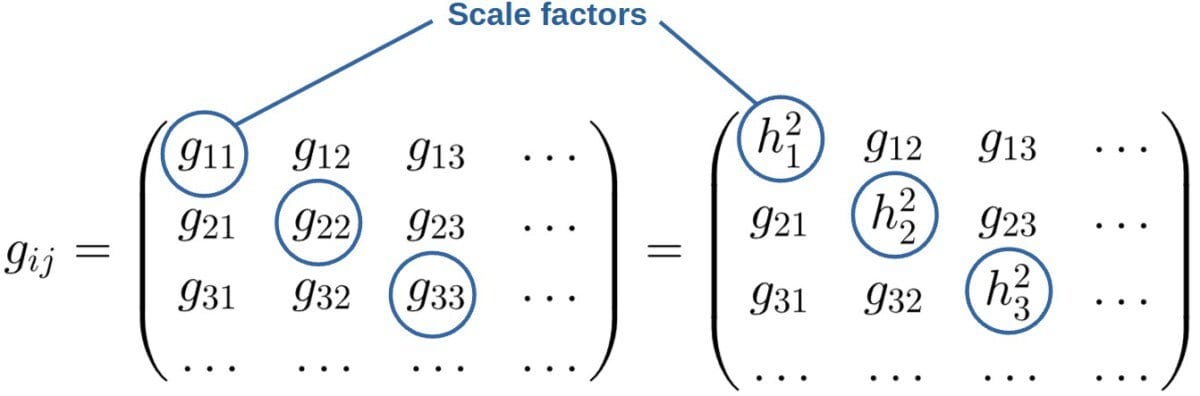
Because of the metric describing dot products between basis vectors, the diagonal elements naturally correspond to the dot product of a given basis vector with itself – which is just its length:

\left|\vec{e}_i\right|=h_i

Scale factors are used quite often used in vector calculus in the context of curvilinear coordinates (coordinate systems with non-constant basis vectors).

For example, it’s possible to define a general formula for the gradient in any orthogonal coordinate system in terms of the scale factors (if you want to know more about this, check out my article Gradient In Different Coordinates):

As an example, if we are in polar coordinates with xⁱ=(x¹,x²)=(r,θ), the scale factors are given by h₁=1 and h₂=r (which can be seen directly from the metric in polar coordinates). Then, we could compute the gradient of some function f as:

\nabla f=\sum_i^{ }\frac{1}{h_i}\frac{\partial f}{\partial x^i}\hat{e}_i=\frac{1}{h_1}\frac{\partial f}{\partial x^1}\hat{e}_1+\frac{1}{h_2}\frac{\partial f}{\partial x^2}\hat{e}_2=\frac{\partial f}{\partial r}\hat{r}+\frac{1}{r}\frac{\partial f}{\partial\theta}\hat{\theta}

Here, \hat{e}_i correspond to the unit basis vectors in the given coordinate system.

Line Elements

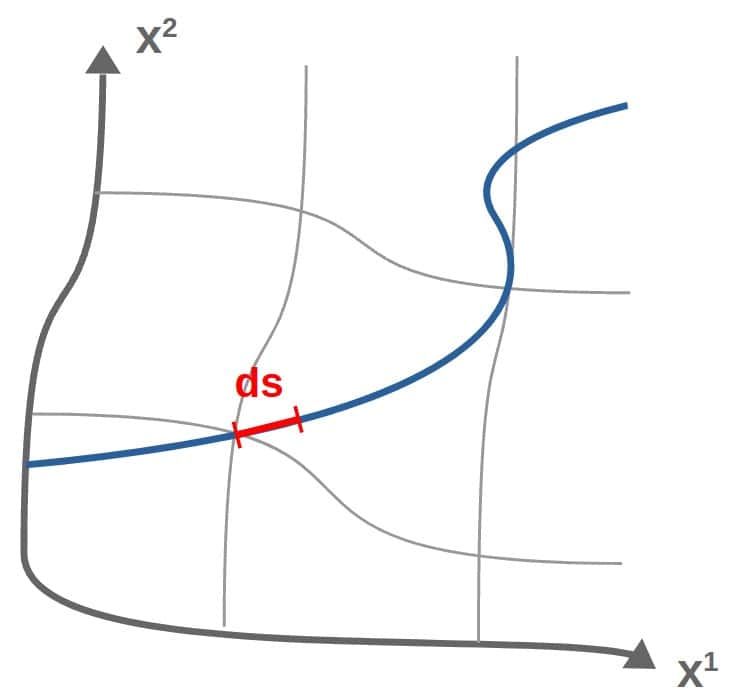
The metric describes lengths of basis vectors and also any other vectors due to its relation with dot products. However, it turns out that it also allows us to describe the length of any curve in any coordinate system or manifold.

The key idea behind this is the so-called line element, which we usually denote as ds² (or ds). The line element describes an infinitesimal length along any curve in any coordinate system:

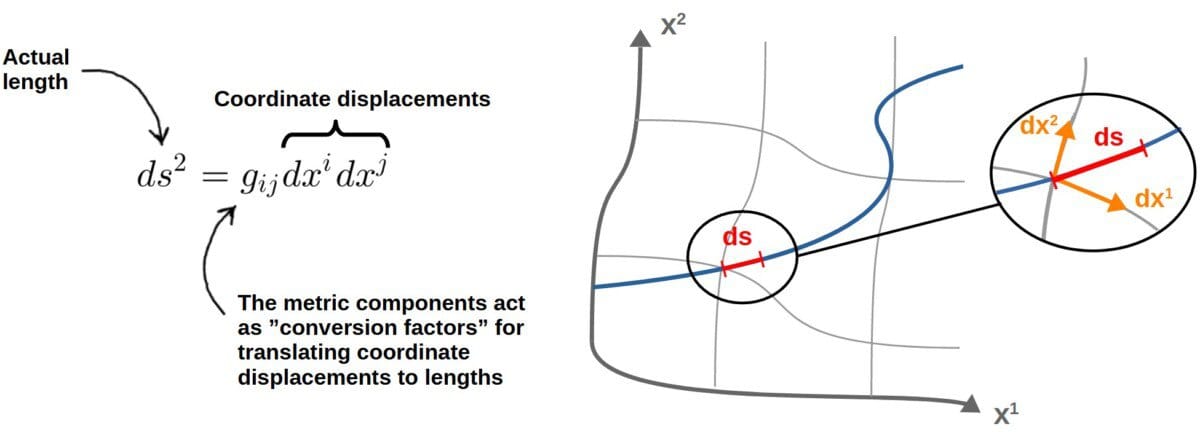
The line element can be calculated from the components of the metric tensor as:

ds^2=g_{ij}dx^idx^j

Here, the dx’s refer to infinitesimal coordinate displacements. For example, in polar coordinates, these would be dr and dθ. We are also using the Einstein summation convention here, meaning that both i and j are summation indices.

The idea here is that these dx’s are displacements in arbitrary coordinates, which do not necessarily have to describe lengths directly, or even have units of length – for example, dθ in polar coordinates describes an angular displacement. So, these coordinate displacements can be anything.

However, what the metric components do is they convert these arbitrary coordinate displacements to actual lengths, described by the line element. This is the idea behind the statement “the metric converts coordinates to lengths”.

In practice, the line element can be used to calculate the arc length of a curve in any coordinate system simply by integrating it along the curve.

Another important use of the line element is that it is actually often used to represent the metric itself. This is because the coordinate displacements (dxⁱ) each define unique directions in a given coordinate system, similar to how the basis vectors do.

Then, writing down the line element also completely specifies the components of the metric in a unique way as well. This is especially common in general relativity, where we often specify the geometry of a given spacetime by writing down the line element.

Determinant of The Metric

The metric tensor, in a particular coordinate system, can be represented as a matrix. Therefore, like any matrix, the metric also has a determinant.

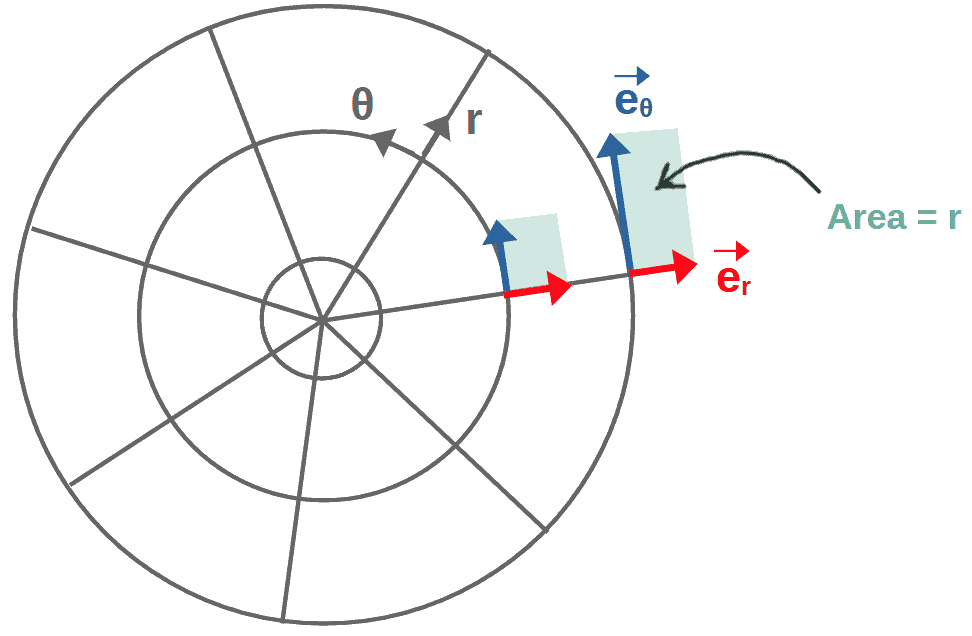
The determinant of the metric tensor describes how areas and volumes are measured in a coordinate system. More precisely, the square root of the metric determinant tells us how areas or volumes scale with the coordinates, and is equivalent to the Jacobian of the coordinate system.

We typically denote the determinant of the metric by the letter g:

g=\det g_{ij}

Now, when we say the determinant of the metric describes how volumes scale with coordinates, we are talking about a piece of volume (or area in 2D) spanned by the basis vectors of the coordinate system.

So, we have a set of basis vectors at each point with some volume in-between them. The metric determinant then describes how this volume scales as we move from point to point:

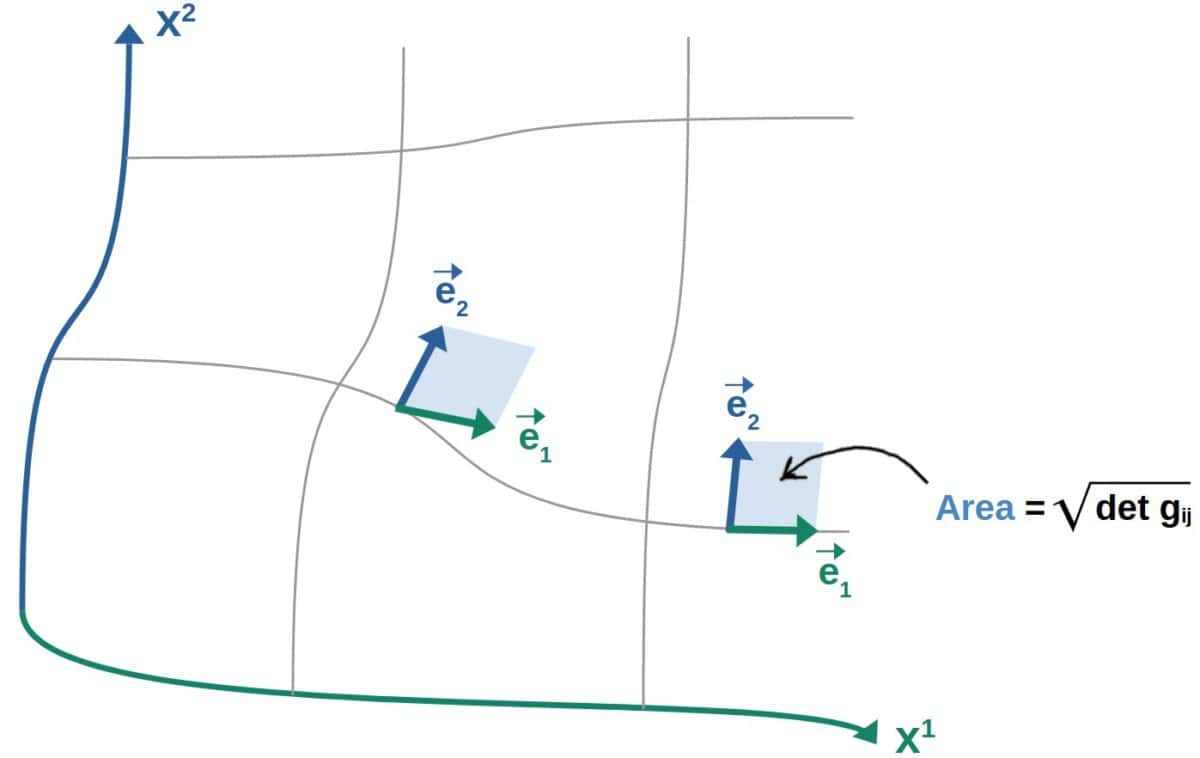
Something worth mentioning here is that, if you’re familiar with multivariable calculus, the interpretation of the metric determinant might seem pretty familiar to the Jacobian. Indeed, the metric determinant is related to the Jacobian as follows:

\sqrt{\det g_{ij}}=J

So, the determinant of the metric tensor is essentially nothing but the Jacobian (or its square).

For orthogonal coordinate systems, the metric determinant is simply the product of its diagonal elements, which means that the Jacobian is directly the product of all scale factors (which can be seen from the polar coordinate example above):

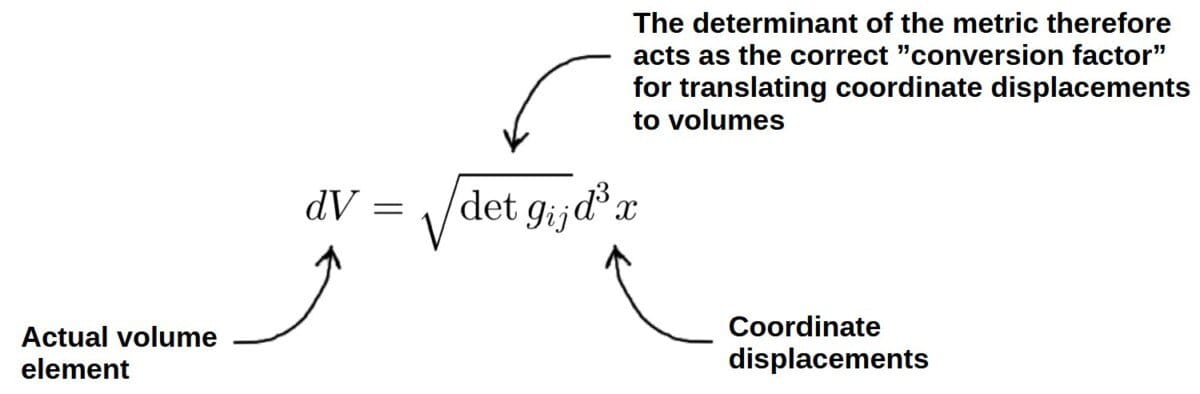
g_{ij}=\begin{pmatrix}h_1^2&0&0&…\\0&h_2^2&0&…\\0&0&h_3^2&…\\…&…&…&…\end{pmatrix}\ \ \Rightarrow\ \ J=\sqrt{\det g_{ij}}=h_1h_2h_3…

Now, because the metric determinant describes this “scaling of volumes”, you’ll often find it appearing in the definition of a volume element in arbitrary coordinates:

dV=\sqrt{\det g_{ij}}d^3x

The d³x here is just notation for the product of coordinate displacements (in 3D) – for example, in Cartesian coordinates, this would be d³x=dxdydz.

The role of the metric determinant here is then to essentially convert coordinate displacements to actual volumes or areas, just like the components of metric convert coordinate displacements to distances:

Physical Meaning of The Metric Tensor

The metric tensor plays a key role in differential geometry, but it is also one of the most important mathematical objects in general relativity.

Physically, the metric tensor can be thought of as representing the gravitational potential in general relativity. This is because it describes the geometry of spacetime and in general relativity, gravity is caused by the curvature of spacetime.

If you’re not familiar with general relativity, I would recommend reading my introductory article on the topic first – you’ll find it here. It should explain everything you need to know to understand this article.

The key idea though is that general relativity describes gravity as an effect arising purely from spacetime being curved. We therefore generally describe spacetime itself as a (four-dimensional) curved manifold.

As we already discussed earlier, the metric tensor is the fundamental tool to describe the geometry of a manifold. Therefore, it automatically plays an important role in describing spacetime curvature just because of its geometric meaning.

Specifically, the metric represents gravitational potentials in general relativity. Now, this interpretation isn’t exactly perfect, but the metric is essentially the closest thing we will get to a fully relativistic gravitational potential.

The simplest way to understand this is by looking at the geodesic equation in the so-called weak-field limit. The weak-field limit is the limit of general relativity for “weak” gravity and it should exactly match with the results obtained from Newtonian gravity.

It turns out that for a radially symmetric mass M (think of a planet, for example), we can derive the following weak-field equation of motion that depends on the 00-component of the metric tensor:

\frac{d^2r}{dt^2}=\frac{c^2}{2}\frac{\partial g_{00}}{\partial r}

Here, r is the radial coordinate (distance from the origin, as measured from the center of the mass M) and c is the speed of light.

In Newtonian gravity, on the other hand, if we write down Newton’s second law (F=ma) for the exact same situation in terms of a gravitational potential (Φ), we have the following equation:

\frac{d^2r}{dt^2}=-\frac{\partial\Phi}{\partial r}

In order for these two equations to match – which they should in the weak-field limit – we make the following identification:

g_{00}=1-\frac{2\Phi}{c^2}

This 1 here is just a constant we are allowed to include in the metric in order for it to reduce to the flat spacetime metric when Φ=0.

We can see from this that the metric is clearly very closely related to the gravitational potential of Newtonian gravity. This analogy is still valid for more complicated spacetimes – the metric is just the “relativistic extension” of the standard gravitational potential.

Another way to understand this is by comparing the Einstein field equations of general relativity to Poisson’s equation from Newtonian gravity.

The Einstein field equations describe the dynamics of the metric for any given spacetime, while Poisson’s equation describes the dynamics of the gravitational potential in a Newtonian setting:

In the Einstein field equations, we basically have “second derivatives of the metric proportional to matter stuff”. On the other hand, with Poisson’s equation, we have “second derivatives of the gravitational potential proportional to matter stuff”.

Therefore, would it not be a reasonable statement to make that the metric indeed is analogous to a gravitational potential of some sort?

Of course, just keep in mind that this is only an interpretation we make and it does not really play any deeper role in general relativity.

Fundamentally, all the geometry behind the metric tensor carries over to general relativity as well, with the addition of an extra time dimension since general relativity deals with spacetime:

• Diagonal elements of a spacetime metric describe lengths of basis vectors in each spacetime direction. An interesting implication of this is that if the component g₀₀ is NOT constant, the “scale” of measurements of time are changing from point to point – we interpret this physically as time dilation.
• Off-diagonal elements of a spacetime metric represent the overlaps of each spacetime basis vector. These are usually zero, but for some more complicated metrics – like the Kerr metric describing rotating black holes – these being non-zero lead to interesting effects like frame dragging.

The Metric Tensor As a Multilinear Map

In many resources on higher-level mathematics like tensor calculus and differential geometry, the metric tensor – and other tensors too – is often described in terms of multilinear maps.

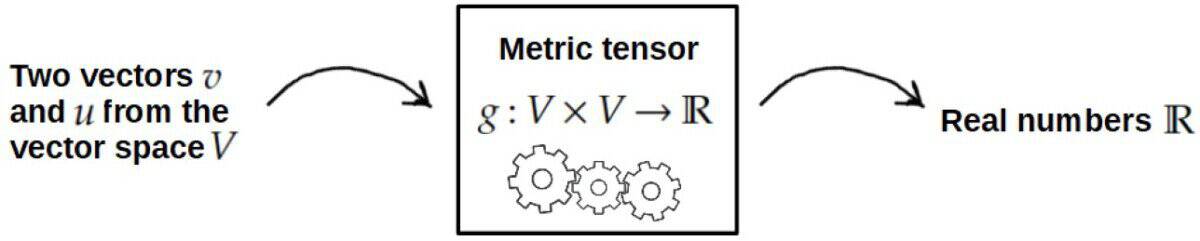
The metric tensor can mathematically be defined as a multilinear map that takes two vectors to a number. This can be understood by the fact that the metric defines the dot product – the dot product is a number resulting from two vectors, which is also what a multilinear map describes.

The basic idea of a multilinear map is that it “maps” a set of vectors to numbers. This is analogous to how an ordinary function maps a number (its input argument) to another number (its output, or the value of the function).

You can therefore think of a multilinear map as a function that takes vectors as its input and outputs a number. The term ‘multi-‘ here refers to the fact that there can be an arbitrary number (multiple) of these input vectors.

In tensor calculus, we have lots of different multilinear maps – in fact, all tensors are multilinear maps. For our purposes, however, the metric tensor is defined as a multilinear map that takes two vectors to a number:

g\left(\vec{v}{,}\vec{u}\right)=\text{number}

When discussing the metric as this abstract multilinear map, we denote it as just g without any indices. In fact, strictly speaking, the g_ij (with indices) from earlier are only referring to the components of the metric in a given coordinate system.

Now, something that takes in two vectors and outputs a number sounds a lot like the dot product. In fact, the action of the metric as a multilinear map on two vectors is how we fundamentally define the dot product:

g\left(\vec{v}{,}\vec{u}\right)=\vec{v}\cdot\vec{u}=g_{ij}v^iu^j

The important point here is that this is a definition. In other words, we can have many different multilinear maps, but the one defined by the metric specifically corresponds to the operation of taking a dot product.

The Inverse Metric Tensor

Another important mathematical object related to the metric tensor is the inverse metric tensor. The inverse metric (its components) is typically denoted with upstairs indices, as g^{ij}.

The way to interpret what the inverse metric actually describes is through the idea of multilinear maps.

Simply put, the inverse metric tensor is mathematically be defined as a multilinear map that takes two covectors to a number. This is analogous to the ordinary metric tensor, except the inverse metric operates on covectors instead of vectors.

Here, I mention the term ‘covector‘. Covectors are another type of mathematical object you’ll encounter very often in tensor calculus. In fact, vectors and covectors are the two fundamental classes of objects pretty much all of tensor calculus is based on.

The reason covectors are relevant is that the inverse metric defines the dot product between two covectors, just like the metric defines the dot product between two vectors:

g^{-1}\left(\tilde{\omega}{,}\tilde{\chi}\right)=\tilde{\omega}\cdot\tilde{\chi}=g^{ij}\omega_i\chi_j=\text{number}

The components of the inverse metric, g^{ij}, are defined analogously to the components of the ordinary metric – as dot products between basis covectors.

On an abstract level, this is saying that the inverse metric is a multilinear map from two covectors to the real numbers. We also refer to such an object as a rank (2,0) tensor.

Just a quick note; there is actually an entire full-length lesson and problem set related to covectors in my Mathematics of General Relativity -course. You might find this useful, if understanding covectors better is relevant for you!

Raising & Lowering Indices With The Metric

In the context of tensor calculus and index notation, you’ll encounter both upstairs and downstairs indices. Then, you’ll come across statements like “the metric is used to raise and lower indices”. But what does this actually mean?

In short, the metric is used to raise and lower indices due to it defining the dot product. Specifically, the metric relates vectors to covectors through the dot product, and if written in index notation, this relation equivalently corresponds to raising and lowering indices.

The way this is used in tensor calculus is as follows:

• Upper indices (= contravariant indices) can be converted to lower indices (= covariant indices) using the metric, like v_i=g_{ij}v^j.

• Lower indices can be converted to upper indices using the inverse metric, like v^i=g^{ij}v_j.

The basic idea is that we have these two types of objects called vectors and covectors (which were discussed earlier), which at first value, are not really related since they live in different vector spaces.

However, if we have a metric that defines a dot product, it turns out that we can, in a sense, relate any vector to a corresponding covector.

This is done by taking the dot product of a vector with a given basis vector. If you think about it, this should give back the component of the vector along the basis vector. But, actually, not quite – it gives the component of the corresponding covector along that basis vector:

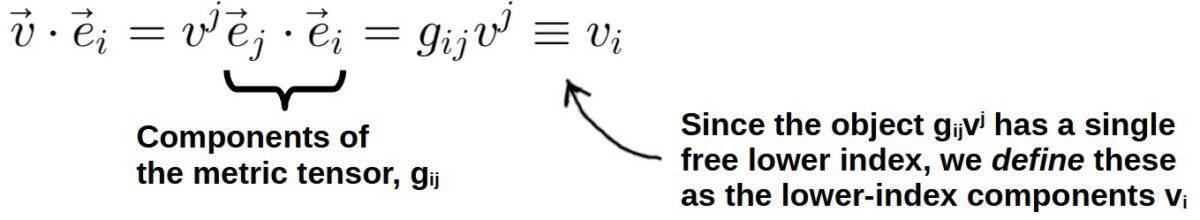
What is really happening here is that the metric defines the dot product between basis vectors and because of this, we are able to take a given vector and calculate the components of the corresponding covector.

Then, when expressed in terms of components in index notation, this is equivalent to first having a vector with components v^j and then converting these to the corresponding covector components v_i – effectively, lowering the index of v^j.

This is the basic idea behind why the metric is used to raise and lower indices – the fundamental reason it works is because the metric is able to naturally relate vectors, covectors and their components.

Is The Metric Actually a Tensor?

The metric tensor is usually referred to as a tensor, but for something to actually be a valid tensor, we need it to satisfy certain properties.

The metric is indeed a tensor because it satisfies all the required properties and characteristics of a valid tensor. These include the metric behaving like a multilinear map and components of the metric transforming like those of a second-rank tensor.

Next, we will briefly discuss what makes a tensor and based on this, go through the arguments for why the metric is a valid tensor.

What Is a Tensor, Anyway?

First, we need to understand what actually makes a valid tensor in the first place. The key properties of a tensor – which it needs to satisfy in order to be a tensor – are the following:

• Tensors are multilinear maps. This means that they take in a set of vectors and covectors and output a number, in a way that is linear in each of the vector and covector arguments.
• The components of tensors transform in very specific way under coordinate transformations. This is sometimes taken as a definition for what a tensor is, but in my opinion, it should better be thought of as just a property.

Something worth noting here is that even though we often represent (second-rank) tensors as matrices, strictly speaking, matrices are not tensors by themselves.

This is because a matrix can, in principle, be any kind of “array of stuff”, but it can only be a tensor if it satisfies the above rules. So, keep in mind this distinction between tensors and matrices – a second-rank tensor can be represented as a matrix, but not all matrices are tensors!

Now, what do we mean by this “very specific way”? Well, if we have set of tensor components in one coordinate system, say T_ij as an example, then after a coordinate transformation, the new components must be obtained as:

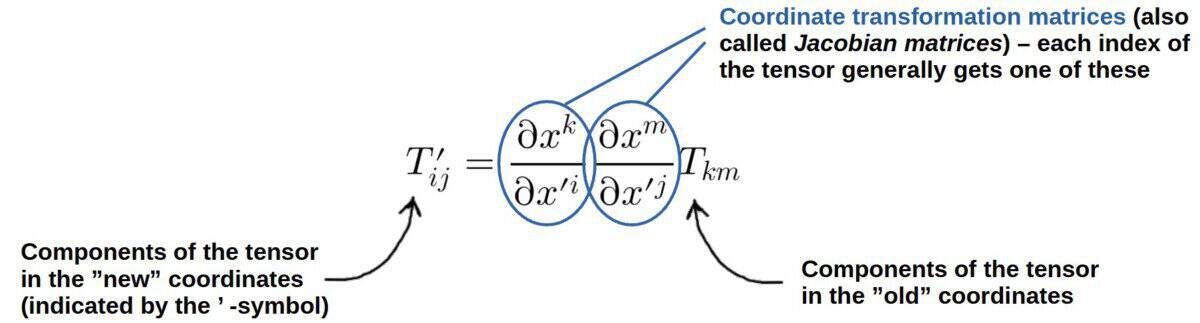
In practice, we usually analyze whether something is a tensor or not by looking at how it transforms under coordinate transformations – if it satisfies the above rule, it is (probably) a valid tensor. If it does NOT, we know with 100 % certainty that it is NOT a valid tensor.

Transformations of The Metric Tensor

For the purposes of this article, we can show that the metric tensor transforms under coordinate transformations as:

g'_{ij}=\frac{\partial x^k}{\partial x'^i}\frac{\partial x^m}{\partial x'^j}g_{km}

This is the transformation rule for the components of a valid second-rank tensor.

We also know that the metric does behave like a multilinear map because of its relation to the dot product – the dot product is a linear operation that takes vectors to a number, which is exactly what a multilinear map is.

Because it satisfies these properties, we can very comfortably conclude that the metric is indeed a perfectly good tensor.

Properties of The Metric Tensor

In this section, we will briefly explore some of the important properties of the metric tensor. We will answer some common questions I’ve been asked previously or encountered elsewhere about the metric.

Is The Metric Tensor Covariant or Contravariant?

The metric tensor is a covariant tensor, meaning a tensor with components that transform covariantly under coordinate transformations. This is because the metric can be defined as the dot product of basis vectors, which are naturally covariant objects.

The terms covariant and contravariant refer to transformation properties of an object under coordinate transformations.

Essentially, an object transforming covariantly transforms with the basis. Think of, for example, basis vectors getting stretched – a coordinate transformation – and a covariant object getting stretched the same way.

On the other hand, an object transforming contravariantly transforms opposite to the basis. Think of basis vectors getting stretched and a contravariant object shrinking in length.

We use index placement to indicate these transformations properties – an object with lower indices transforms covariantly, while an object upper indices transforms contravariantly. Something with both (mixed) indices would transform in a combination of both ways.

Now, the metric itself (which has components g_ij) naturally has lower indices for its components and it transforms covariantly – thus, it is a covariant object. The inverse metric (with components g^ij), however, transforms in the opposite way – contravariantly. Therefore:

• The metric tensor itself is naturally covariant.
• The inverse metric tensor is contravariant.

Are All Metric Tensors Diagonal?

Not all metric tensors are diagonal. In fact, metric tensors are only diagonal in orthogonal coordinate systems, where all basis vectors are perpendicular to one another. A famous example of a metric that is not diagonal is the Kerr metric, describing a rotating black hole.

The key point here is that whether a metric is diagonal or not, depends directly on the coordinate system and the basis we construct for it. If we have a coordinate system with basis vectors that are NOT orthogonal, the metric will have non-zero off-diagonal components:

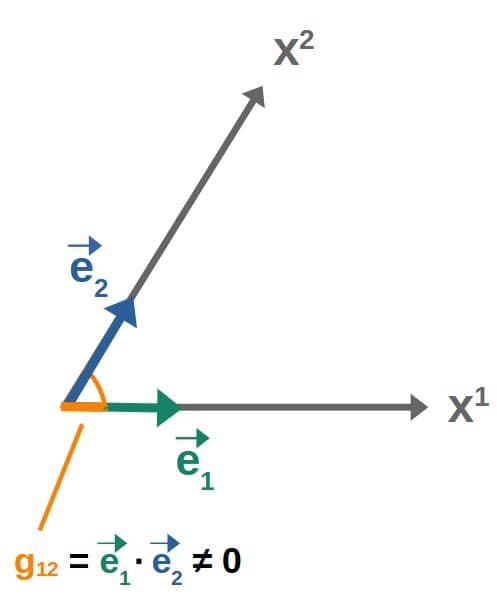
Now, most of the metrics you’ll encounter in physics and elsewhere are going to be diagonal, simply because orthogonal coordinate systems are typically much more useful and convenient to work with.

However, some special metrics like the Kerr metric from general relativity – which you will find later in this article – do have off-diagonal components due to the physics or geometry they describe.

For example, the Kerr metric not being diagonal reflects the frame dragging effect that occurs in the Kerr spacetime around a rotating black hole.

Does The Metric Have To Be Symmetric?

The metric tensor is always symmetric, meaning the relation g_ij=g_ji is always true for its components. Intuitively, the reason for this is that the metric measures the alignment of basis vectors in a given coordinate system, which is irrelevant of the order in which the alignment is measured.

The simplest way to understand why the metric is symmetric is to look at its definition in terms of dot products between basis vectors, g_{ij}=\vec{e}_i\cdot\vec{e}_j.

Mathematically, we know the dot product is a symmetric operation, which must make the metric symmetric as well. But why is this true, geometrically speaking? Well, the easiest way to see why this makes sense is to consider two orthogonal basis vectors, meaning the metric component g₁₂ is zero:

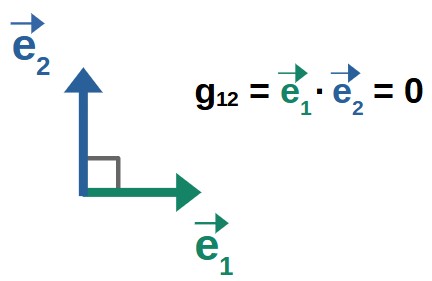
The metric component g₁₂ here measures the alignment of the basis vector e₁ with respect to e₂. Now, consider measuring the alignment in the opposite way – the alignment of e₂ with respect to e₁, described by the metric component g₂₁.

Clearly, the basis vectors are still orthogonal – irrespective of which order the alignment is measured in – so the result is that g₁₂=g₂₁=0. So, the metric is symmetric (at least in this case).

• This property of the metric being symmetric does indeed hold in all other cases as well. In fact, the metric is, by definition, taken to always be symmetric.
• Some physicists have considered theoretical metrics that are not symmetric, however, strictly speaking, these cannot really be considered metric tensors anymore.

What Are The Units of The Metric?

In principle, the units of the metric tensor can be anything, provided that the product of each metric component with the corresponding coordinate displacement results in something with units of length. In other words, the coordinate system being used determines the units of the metric.

At surface value, this idea comes from the fact that the metric components appear in the line element with the “square” of coordinate displacements:

ds^2=g_{ij}dx^idx^j

Because ds² represents the square of a distance element, it has units of distance squared. However, the coordinate displacements can be anything, so they can have any units (for example, in polar coordinates, we have both dr – something with units of length – and dθ, which is dimensionless).

Therefore, the rule is that for any two arbitrary coordinate displacements, dx¹ and dx², the product g₁₂dx¹dx² must have units of length squared – thus, the metric converts coordinates to distances, unit-wise as well.

Above, I mentioned “at surface value” – this is because there are actually a few different conventions being used for the units of the metric:

• Some authors take the metric to always be dimensionless. This requires the coordinate displacements to be scaled such that they all have units of length.
• Some authors take the metric – all of its components – to have units of length. This requires making the coordinates dimensionless.
• The general rule, however, is that the line element (ds²) calculated from the metric, and correspondingly, all terms in it have units of length regardless of which of these conventions is being used.

Metric Tensor Examples: A Complete List

In this section, we’ll look at some examples of metric tensors. These are all the most commonly used metrics you’ll come across in both differential geometry and general relativity.

For each metric, I’ll present the used coordinates, line element, metric components in matrix form and some general remarks or noteworthy points about the metrics.

When looking at the list of the various metrics, I recommend keeping in mind the interpretation of each component like we discussed earlier in this article:

• The diagonal metric components describe lengths of basis vectors – in a sense, how each coordinate direction “scales” as you move around the coordinate system.
• The off-diagonal metric components represent the overlap of basis vectors – notably, if there are non-zero off-diagonal components, it means that the coordinate system being used is not orthogonal and the coordinate directions, in a sense, overlap with one another.

This section is meant to be a reference resource – a big list of metrics you can refer back to whenever needed. I suggest saving the link to this page, so you can come back to it later.

If you’re interested in a similar list of the most common Christoffel symbols, check out the end of this article.

Metric In Cartesian Coordinates

This first example is by far the simplest one – the usual Cartesian coordinate system. The Cartesian coordinate system consists of three orthogonal coordinate directions; x, y and z.

In Cartesian coordinates, the line element is given simply by the standard 3-dimensional Pythagorean theorem:

ds^2=dx^2+dy^2+dz^2

The metric is therefore just a bunch of ones and zeroes – often also denoted as δ_ij – which can be written in matrix form as:

g_{ij}=\delta_{ij}=\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}

Metric In Polar Coordinates

In polar coordinates, all points are described by two coordinates (since polar coordinates, by definition, are a two-dimensional coordinates system), r and θ. A polar coordinate system still corresponds to flat space, not a curved one.

The line element in polar coordinates is given by:

ds^2=dr^2+r^2d\theta^2

The metric components, therefore, written in matrix form are:

g_{ij}=\begin{pmatrix}1&0\\0&r^2\end{pmatrix}

Note here that, unlike the Cartesian metric, the metric components in polar coordinates are not constant – g₂₂ depends on the radial distance from the origin. This is because the angular basis vector naturally has a length of r, not 1.

Metric In Spherical Coordinates

The spherical coordinate system is another example of a flat space that is represented in different coordinates than Cartesian coordinates.

Spherical coordinates are the analogue of polar coordinates, but in three dimensions. All points in the spherical system are described by three coordinates, r, θ and φ – a radial distance and two angles. The line element is given by:

ds^2=dr^2+r^2d\theta^2+r^2\sin^2\theta d\varphi^2

The metric components are therefore:

g_{ij}=\begin{pmatrix}1&0&0\\0&r^2&0\\0&0&r^2\sin^2\theta\end{pmatrix}

Metric In Cylindrical Coordinates

The cylindrical coordinate system is equivalent to the spherical one, in the sense that both describe space in three dimensions using three coordinates.

In the case of cylindrical coordinates, however, we have the coordinates r, φ and z – a radial distance, and angle (which is the same as the polar angle) and the same z-coordinate as in Cartesian coordinates.

The line element in cylindrical coordinates is given by:

ds^2=dr^2+r^2d\varphi^2+dz^2

The metric components are:

g_{ij}=\begin{pmatrix}1&0&0\\0&r^2&0\\0&0&1\end{pmatrix}

Notice how this is basically the polar metric, but with the Cartesian z-direction tagged on.

Metric On a Sphere

This example describes the metric for a sphere in three dimensions or more accurately, a 2-sphere, which is the 2-dimensional surface of a 3-dimensional sphere. This is also our first example of a curved space.

Since this is a sphere we’re describing and a sphere is characterized by some constant radius from the origin, the 2-sphere actually has the same metric as in spherical coordinates, but with r=R taken as a constant, NOT a coordinate (and dr=0):

ds^2=R^2d\theta^2+R^2\sin^2\theta d\phi^2

We therefore have only two metric components (since there are only two coordinates):

g_{ij}=\begin{pmatrix}R^2&0\\0&R^2\sin^2\theta\end{pmatrix}

Metric On a Torus

A torus is quite a peculiar geometric shape – basically a donut – that can be characterized by two coordinates, u and v, and two constant parameters, the major radius R and the minor radius r (for a visual picture of what these represent, you can check out this paper).

The line element using these coordinates and parameters is given by:

ds^2=\left(R+r\cos v\right)^2du^2+r^2dv^2

The metric components are therefore:

g_{ij}=\begin{pmatrix}\left(R+r\cos v\right)^2&0\\0&r^2\end{pmatrix}

The Schwarzschild Metric

The Schwarzschild metric is perhaps the most famous solution to the Einstein field equations of general relativity. It describes the spacetime around a static, spherically symmetric mass (for example, a planet or black hole). This is our first example of a spacetime – curved, as well.

The most common way to represent the Schwarzschild metric is by using the so-called Schwarzschild coordinates (ct, r, θ and φ). In these coordinates, the line element is given by:

ds^2=-\left(1-\frac{r_s}{r}\right)c^2dt^2+\left(1-\frac{r_s}{r}\right)^{-1}dr^2+r^2d\theta^2+r^2\sin^2\theta d\varphi^2

Here, r_s is a parameter called the Schwarzschild radius and it is given by:

r_s=\frac{2GM}{c^2}

Here, G is the gravitational constant, M is the mass of the central body causing the gravitational field and c is the speed of light.

The metric components can also be written in matrix form as:

g_{\mu\nu}=\begin{pmatrix}-\left(1-\frac{r_s}{r}\right)&0&0&0\\0&\left(1-\frac{r_s}{r}\right)^{-1}&0&0\\0&0&r^2&0\\0&0&0&r^2\sin^2\theta\end{pmatrix}

Note; here I’m using Greek indices instead of Latin ones since we’re now in 4 spacetime dimensions.

A noteworthy point about this metric is that something quite weird happens at r=r_s:

• At r=r_s, the time component of the metric goes to zero, which essentially means the time direction “shrinks” to zero – it would take an infinite amount of the time coordinate to represent a finite time interval. We interpret this as infinite time dilation.
• At r=r_s, the radial component of the metric goes to infinity. We can similarly interpret this as “infinite length contraction”.
• Generally, the point r=r_s is the event horizon of the mass M. For “small” masses like stars or planets, this would be inside the mass, which practically means the event horizon does not exist.

The Kerr Metric

The Kerr metric is another solution to the Einstein field equations, which describes the same type of spacetime as the Schwarzschild metric, except that the Kerr metric allows for the central mass to be rotating. So, the Kerr metric is a more general metric for describing planets, stars and black holes.

The line element for this metric can be written in so-called Boyer-Lindquist coordinates (a form of spherical coordinates with the coordinates ct, r, θ and φ) as:

ds^2=-\left(1-\frac{r_sr}{\Sigma}\right)c^2dt^2-\frac{2r_sra\sin^2\theta}{\Sigma}cdtd\varphi+\frac{\Sigma}{\Delta}dr^2+\Sigma d\theta^2+\left(\mu+\frac{r_sra^2\sin^2\theta}{\Sigma}\right)\sin^2\theta d\varphi^2

A noteworthy point about this metric is the cross-term between the time-coordinate ct and the angular coordinate φ; this is due to the fact that a rotating mass causes a so-called frame dragging effect in the spacetime around it. This, on the other hand, causes an additional time dilation effect, which can be seen from this coupling term between the angular displacement, dφ and the “displacement in time, dt”. I actually discuss frame dragging and its effects on time dilation in this article.

The various parameters you see here are length scales of the Kerr spacetime (they all have units of length) defined by (with r_s being the usual Schwarzschild radius 2GM/c²):

a=\frac{J}{Mc}\\ \mu=r^2+a^2\\ \Sigma=r^2+a^2\cos^2\theta\\ \Delta=r^2+a^2-r_sr

The metric components can be represented in matrix form as:

g_{\mu\nu}=\begin{pmatrix}-\left(1-\frac{r_sr}{\Sigma}\right)&0&0&-\frac{r_sra\sin^2\theta}{\Sigma}\\0&\frac{\Sigma}{\Delta}&0&0\\0&0&\Sigma&0\\-\frac{r_sra\sin^2\theta}{\Sigma}&0&0&\left(\mu+\frac{r_sra^2\sin^2\theta}{\Sigma}\right)\sin^2\theta\end{pmatrix}

Note that the metric is not diagonal in this case, since it has the t,φ cross-terms, which reflect the frame dragging effect.

Notice that the Kerr metric reduces to the Schwarzschild metric in the case that a=0 – the black hole is fully stationary. Therefore, the Kerr metric is a generalization of the Schwarzschild metric.

The Reissner-Nordström Metric

The Reissner-Nordström metric is another solution to the Einstein field equations, belonging to the same “class” of metrics as the Schwarzschild and Kerr metrics (by “class”, I mean the different black hole type solutions of general relativity).

This metric describes a spherically symmetric and electrically charged (but non-rotating) mass. The line element can be written using the coordinates ct, r, θ and φ as:

ds^2=-\left(1-\frac{r_s}{r}+\frac{r_Q^2}{r^2}\right)c^2dt^2+\left(1-\frac{r_s}{r}+\frac{r_Q^2}{r^2}\right)^{-1}dr^2+r^2d\theta^2+r^2\sin^2\theta d\varphi^2

Here, r_s is again the Schwarzschild radius and r_Q^2 is a parameter related to the charge of the central mass:

r_Q^2=\frac{Q^2G}{4\pi\varepsilon_0c^4}

Here, Q is the charge of this mass, G is the gravitational constant, c is the speed of light and ε₀ is the vacuum permittivity (another constant).

The metric components are:

g_{\mu\nu}=\begin{pmatrix}-\left(1-\frac{r_s}{r}+\frac{r_Q^2}{r^2}\right)&0&0&0\\0&\left(1-\frac{r_s}{r}+\frac{r_Q^2}{r^2}\right)^{-1}&0&0\\0&0&r^2&0\\0&0&0&r^2\sin^2\theta\end{pmatrix}

Notice that this reduces to the Schwarzschild metric again when Q=0.

The Weak-Field Metric

The weak-field metric is a solution of general relativity in the limit that gravity is not “too strong” (more formally, that the metric only deviates slightly from the flat spacetime Minkowski metric; by slightly, I mean that the deviations only count to linear order).

Another important aspect of this limit is we also assume that velocities are relatively small (this means that the ratio v/c can be approximated as zero and dt/dτ≈1).

Anyway, the line element can be written in spherical coordinates as (you may also see it written in Cartesian coordinates):

ds^2=-\left(1+\frac{2\Phi}{c^2}\right)c^2dt^2+\left(1-\frac{2\Phi}{c^2}\right)dr^2+\left(1-\frac{2\Phi}{c^2}\right)r^2d\theta^2+\left(1-\frac{2\Phi}{c^2}\right)r^2\sin^2\theta d\varphi^2

Here, Φ is the Newtonian gravitational potential, given by \Phi=-\frac{GM}{r}. The metric can also be written in the matrix form:

g_{\mu\nu}=\begin{pmatrix}-\left(1+\frac{2\Phi}{c^2}\right)&0&0&0\\0&1-\frac{2\Phi}{c^2}&0&0\\0&0&\left(1-\frac{2\Phi}{c^2}\right)r^2&0\\0&0&0&\left(1-\frac{2\Phi}{c^2}\right)r^2\sin^2\theta\end{pmatrix}

Notice that in the case of Φ=0, this reduces to the standard flat spacetime metric for spherical coordinates. Therefore, with the assumption that Φ is relatively small, this describes a “small deviation” from the flat spacetime metric.

In fact, you’ll sometimes find this metric also written in the form g_{\mu\nu}=\eta_{\mu\nu}+h_{\mu\nu}, where \eta_{\mu\nu} is the Minkowski metric describing the flat spacetime of special relativity and h_{\mu\nu} represents the weak-field corrections:

\eta_{\mu\nu}=\begin{pmatrix}-1&0&0&0\\0&1&0&0\\0&0&r^2&0\\0&0&0&r^2\sin^2\theta\end{pmatrix} h_{\mu\nu}=\begin{pmatrix}-\frac{2\Phi}{c^2}&0&0&0\\0&-\frac{2\Phi}{c^2}&0&0\\0&0&-\frac{2\Phi}{c^2}r^2&0\\0&0&0&-\frac{2\Phi}{c^2}r^2\sin^2\theta\end{pmatrix}

The Robertson-Walker (FRW) Metric

The Robertson-Walker metric (often called the FRW metric) describes what is called a maximally symmetric spacetime – one that is both homogeneous and isotropic.

This metric can, for example, describe our universe on a large scale, and it is used to predict things like the expansion of the universe.

I discuss the FRW metric, its associated Friedmann equations and their predictions more in this article, in case you’re interested.

The line element for the FRW metric using the coordinates ct, r, θ and φ is:

ds^2=-c^2dt^2+\frac{a^2\left(t\right)}{1-kr^2}dr^2+a^2\left(t\right)r^2d\theta^2+a^2\left(t\right)r^2\sin^2\theta d\phi^2

Here, k is a curvature parameter that can take on the values -1, 0 or 1, depending on the geometry of the spacetime (to describe a flat universe, k=0, for example). The a(t)-parameter is called the scale factor and it is a function of time that holds information about the expansion of the universe (or whatever space this metric happens to be describing).

This metric has the matrix form:

g_{\mu\nu}=\begin{pmatrix}-1&0&0&0\\0&\frac{a^2}{1-kr^2}&0&0\\0&0&a^2r^2&0\\0&0&0&a^2r^2\sin^2\theta\end{pmatrix}