Why Is Momentum Conserved But Kinetic Energy Is Not? (with examples!)
Intuitively, momentum and kinetic energy are both about speed and how much mass something has – if you increase either the speed or mass of an object, it gains more kinetic energy and momentum. In this sense, they share a lot of similarities, so when then is momentum conserved but kinetic energy is not?
Kinetic energy by itself is not conserved simply because energy can always change form – from kinetic to potential and back or to any other form of energy. However, the total momentum is always conserved in a closed system and likewise, total energy is always conserved in an isolated system.
In this article, we’ll clarify the reasons behind both the conservation of momentum and energy and go through some examples of how energy itself changes form – so we’ll see explicitly how in some cases, kinetic energy is conserved but in others it is not – whereas momentum always is!
If you’re interested in a full comparison between kinetic energy and momentum, you can check out this article. The article also covers some of the differences between these quantities that become important in other areas of physics, like relativity and quantum mechanics.
Also, if you’re interested in learning physics more deeply, you may enjoy my Advanced Math For Physics: A Complete Self-Study Course – it’s the perfect place to get started learning more advanced physics and math!
Conservation of Momentum and Energy
Let’s start with momentum. We can visualize this as the quantity that keeps an object going. If there were two cars rolling down a hill at equal speed but they had different masses, the heavier car would be much harder to stop.
Mathematically, we define momentum, p, in terms of an object’s mass, m, and velocity, v:
\vec{p}=m\vec{v}The arrows on top of the symbols for momentum and velocity represent the fact that these are vector quantities.
A vector is a quantity that has both a magnitude (a size) and a direction. Going back to our car analogy, the direction is encoded in the fact that the momentum is clearly pointed down the hill.
Now we know what momentum is, but what does it mean for it to be conserved?
A conserved quantity in physics means that it does not change in time. That is to say, if you had a counter that showed you the total momentum in a system, no matter what time you go back and check the counter, it will always say the same amount.
We know what conservation is – and that momentum itself is conserved – but why is it conserved?
Let’s go back to Newton. As you might know, Newton came up with three laws of motion. The second two are of particular importance to us:
- Second Law: Force is the rate of change of momentum
- Third Law: Every action has an equal and opposite reaction
Consider two objects. They both will have their own momenta. According to Newton’s second law, this will define the force they can exert.
If the two objects collide, then they will exert equal and opposite forces on each other. This means that whatever momentum (by exerting the force) is lost by one object will be gained by the other and vice-versa.
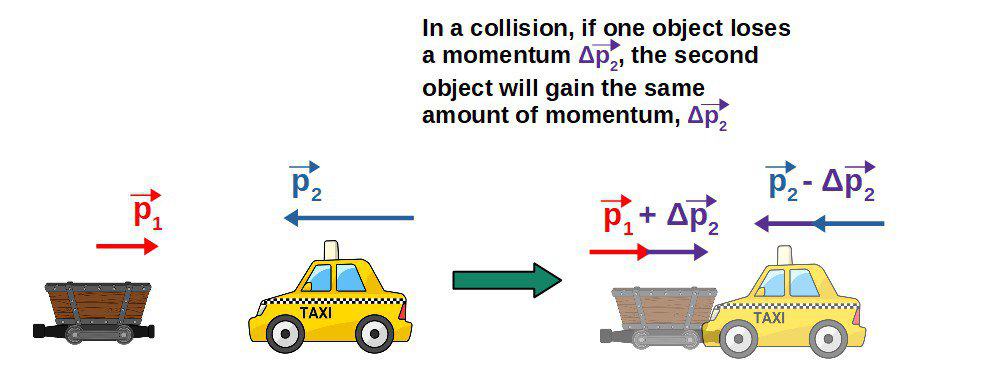
What does this tell us? If the amount of momentum gained by one object is equal to that lost by another, then the total momentum before and after the interaction was the same.
This is exactly what our definition of conservation was!
If we start from just Newton’s laws, we can derive an expression for the conservation of momentum.
The simplest case to consider is two balls moving in a straight line towards each other – this is a 1D example but it can generalise quite easily (though the generalisation isn’t necessary to show the maths!)
Let’s call these ball 1 and ball 2 and label their momenta as such, p1 and p2.
What happens when two balls interact? They exert a force on each other.
The most famous of Newton’s laws is his second:
\vec{F}=m\vec{a}This can be restated in a slightly different way instead as the time derivative of an object’s momentum.
This follows from the fact that acceleration is the time derivative of the velocity. Plus, mass is constant so we can bring it under the derivative, hence:
\vec{F}=m\vec{a}=m\frac{d\vec{v}}{dt}=\frac{d\left(m\vec{v}\right)}{dt}=\frac{d\vec{p}}{dt}With this in mind, we can now appeal to Newton’s third law – the forces exerted by the balls are equal and opposite. Hence:
\frac{d\vec{p_1}}{dt}=-\frac{d\vec{p_2}}{dt}\Rightarrow\frac{d}{dt}\left(\vec{p_1}+\vec{p_2}\right)=0We can see from this equation that from just Newton’s laws, the total momentum, which in this case is p1+p2, has vanishing time derivative. We before defined conservation as the total momentum not changing in time and this is exactly what a vanishing time derivative tells us!
Now let’s move onto the conservation of energy.
Energy has many different forms: kinetic, chemical potential, gravitational potential, elastic potential and thermal just to name a few!
Energy can change between these different forms when something does work.
Work is the transfer of energy – for example, you do work when lifting an object as this converts kinetic energy into gravitational potential energy.
Taking this, we can define energy as the ability to do work!
With our heads wrapped around the concept of energy, we can address its conservation. You might have heard the phrase “Laws of Thermodynamics”.
The Second Law of Thermodynamics is by far the most popularly quoted, stating that total “entropy” cannot decrease. However, it is the First Law of Thermodynamics that we’re interested in – it is this law that tells us that the total energy in a system is constant.
If something is constant, it means that it does not change in time and this fits in exactly with our definition of something being conserved!
How can we conceptualize the conservation of energy? Think of trying to destroy something and, whatever you do, you can always describe the changes in energy. For example:
- Burning a piece of paper: paper has chemical energy and when you set it alight, it releases this as thermal energy which heats the air around it – overall, no energy is destroyed!
You can describe the energy transfers that happen in everything you do (at least theoretically, you could)! As I write this article, chemical energy in my body is being transferred to kinetic energy to type!
At this point, we have an implicit understanding of why kinetic energy is not conserved – it is just one form of energy, which means that it can be transformed into other forms of energy such that the total energy is always conserved.
So, the bottom line is this:
- Momentum is a conserved quantity – this is a direct result of Newton’s laws.
- Kinetic energy is NOT conserved in general, but total energy is – this is because kinetic energy may be converted to other forms of energy and is thus, not conserved. However, total energy still is.
Noether’s Theorem For Momentum and Kinetic Energy Conservation
Noether’s theorem is one of the most fundamental theorems having to do with conservation laws. Noether’s theorem can also help us understand how the conservation of momentum and kinetic energy differ and why.
Essentially, Noether’s theorem states that for every symmetry in the laws of physics of a system, there exists an associated conservation law. For example, if a system has a translational symmetry, it means that the total momentum will be conserved.
In modern physics, Noether’s theorem IS the fundamental way in which we define conservation laws, so if a conservation law exists, it is simply because Noether’s theorem predicts so.
If you want to learn more about Noether’s theorem specifically, I recommend reading my complete guide on it here.
Noether’s theorem is based on an area of classical mechanics known as Lagrangian mechanics. You can read an introduction to Lagrangian mechanics here.
You can also watch this short video explaining the basic idea of Noether’s Theorem:
The key point about Noether’s theorem is that it states that there exists a conservation law for momentum. Namely, momentum conservation is related to spacial translation and symmetries associated with spacial translation.
On the other hand, there is no conservation law for kinetic energy according to Noether’s theorem. There is certainly a conservation law for total energy, but not specifically to kinetic energy.
Now, in some cases, if the only form of energy an object has is kinetic energy (and probably mass as well), then the conservation of total energy will correspond to kinetic energy being conserved.
In other words, there are certain situations where kinetic energy is conserved, but it is not necessarily always conserved while momentum, on the other hand, is always conserved.
We’ll now explore some examples to see all of this in action. The purpose of these examples is to illustrate how in some cases, kinetic energy can be conserved while in other cases, it is not. Regardless, momentum is still conserved.
If you're interested in a deeper look at the differences between momentum and kinetic energy (such as how they differ in special relativity), I'd recommend reading this article. Another interesting aspect of momentum and kinetic energy not discussed in this article is the fact that massless objects like photons can still have momentum and kinetic energy. If you want to know how that's possible, you can read this article.
Examples of Kinetic Energy and Momentum Conservation
Collisions between objects can be roughly categorized as elastic or inelastic. Let’s explore them both!
Elastic Collision
An elastic collision is one where kinetic energy is, in fact, conserved.
Imagine playing snooker or pool. When one ball hits another, this is (to a very good approximation) an example of an elastic collision, since no energy is lost via heat or by other means transformed away from kinetic energy.
We can see this mathematically:
| Ball 1 Before Collision | Ball 2 Before Collision | Ball 1 After Collision | Ball 2 After Collision | |
| Mass | m_1 | m_2 | m_1 | m_2 |
| Velocity | \vec{v}_1 | \vec{v}_2 | \vec{u}_1 | \vec{u}_2 |
| Momentum | \vec{p}_1=m_1\vec{v}_1 | \vec{p}_2=m_2\vec{v}_2 | \vec{q}_1=m_1\vec{u}_1 | \vec{q}_2=m_2\vec{u}_2 |
| Kinetic Energy | T_1=\frac{1}{2}m_1v_1^2 | T_2=\frac{1}{2}m_2v_2^2 | \tilde{T}_1=\frac{1}{2}m_1u_1^2 | \tilde{T}_2=\frac{1}{2}m_2u_2^2 |
Momentum is always conserved, so we have the following restriction:
\vec{p_1}+\vec{p_2}=\vec{q_1}+\vec{q_2}\Rightarrow m_1\vec{v_1}+m_2\vec{v_2}=m_1\vec{u_1}+m_2\vec{u_2}Along with the conservation of kinetic energy in this case:
T_1+T_2=\tilde{T}_1+\tilde{T}_2\Rightarrow\frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2=\frac{1}{2}m_1u_1^2+\frac{1}{2}m_2u_2^2What do these do for us? They in fact solve the problem for us!
It is not immediately obvious how though. If we have some initial data, say the masses and pre-collision velocities, then the two conservation equations tell us what the post-collision velocities must be.
To be clearer, we could rearrange the momentum equation to get:
\vec{u_2}=\frac{1}{m_2}\left(m_1\vec{v_1}+m_2\vec{v_2}-m_1\vec{u_1}\right)\Rightarrow u_2^2=\frac{1}{m_2^2}\left(m_1\vec{v_1}+m_2\vec{v_2}-m_1\vec{u_1}\right)^2Then by plugging this into the kinetic energy equation, gives us an equation for u1 that we could solve. Then by plugging in the value of u1 into the above equation, we find our value of u2 and thus, we find the velocities of the balls after the collision!
The main point here, however, is that because there is no transform of kinetic energy to other forms of energy, kinetic energy is conserved (along with momentum). This is the special property of elastic collisions.
Inelastic Collision
On the other hand, an inelastic collision is one where momentum is conserved but kinetic energy is not.
The simplest example of this is when two objects collide and get “stuck” together. This is what we call a perfectly inelastic collision.
Kinetic energy is lost here by joining the two bodies together. Imagine a really sticky ball being thrown at another object, say, a toy car – they stick together and this sticking results in the transformation of kinetic energy into other forms.
We can draw a similar table and see that this still has enough information to solve the problem:
| Sticky Ball | Toy Car | Combined Object (after collision) | |
| Mass | M_1 | M_2 | M=M_1+M_2 |
| Velocity | \vec{V}_1 | \vec{V}_2 | \vec{V} |
| Momentum | \vec{P}_1=M_1\vec{V}_1 | \vec{P}_2=M_2\vec{V}_2 | \vec{P}=M\vec{V}=\left(M_1+M_2\right)\vec{V} |
And we can combine this with the conservation of momentum (remember, momentum is always conserved):
\vec{P_1}+\vec{P_2}=\vec{P}\Rightarrow M_1\vec{V_1}+M_2\vec{V_2}=M\vec{V}=\left(M_1+M_2\right)\vec{V}And this conservation law is enough to solve our dynamics! If we divide by (M1+M2), we have solved for the velocity V of the combined ball-and-car object:
\vec{V}=\frac{M_1\vec{V}_1+M_2\vec{V}_2}{M_1+M_2}This is exactly why conservation laws are so important. They constrain systems, allowing us to say exactly what their resulting dynamics should be.
Again, the main point in this example is to show that while momentum is still conserved, kinetic energy is not. This is because of the fact that the objects collide and get stuck together, which results in all kinds of energy “losses” to heat, sound and so on.
Energy Conservation in a Gravitational Field
We’ve had a look at using both the conservation of energy and the conservation of momentum together in two body collisions. Let’s focus finally on just energy and see the conversion of kinetic energy – this shows an example of what actually happens to kinetic energy when it’s not conserved.
Imagine a ball that is being thrown in a straight line upwards. It starts with some initial speed, slows down until it stops at the top of its trajectory, before it falls back down.
What governs this whole system is the conservation of energy.
The equation governing this is simply “total energy = kinetic energy + gravitational potential energy”, or as an equation:
E=\frac{1}{2}mv^2+mghHere v is the velocity of the ball, g is a constant with a value around 9.81 m/s2 that tells us how strong gravity is on Earth, h is the height of the ball, m is the mass of the ball and E is the total energy.
The velocity of the ball changes over time. As I said before, it has an initial value, it slowly decreases until it hits zero, and then increases again as the ball falls back down.
If we think about the different types of energies throughout the trajectory, the ball starts with maximum kinetic energy right when it is thrown up (because afterwards it slows down) and slowly, kinetic energy is transformed into gravitational potential energy.
At the top, the ball has maximum gravitational potential energy and zero kinetic energy because it has stopped moving for a moment. Then, slowly as the ball falls, its gravitational potential energy is transformed into kinetic energy again.
This conversion of kinetic energy into potential energy happens because the force of gravity does work on the ball. If you want to know how this actually happens in practice, you can check out this article. The article also covers some interesting examples of energy conversion in different gravitational systems.
The total energy E (which is a constant) determines how high the ball can go. We can see this in the following:
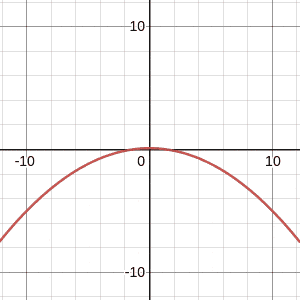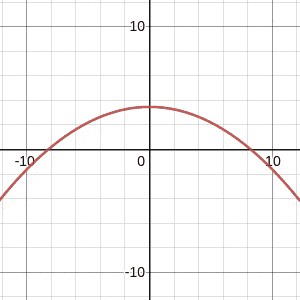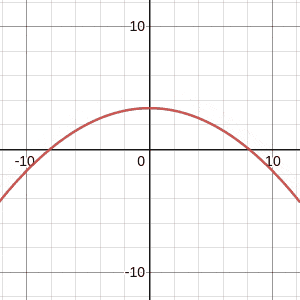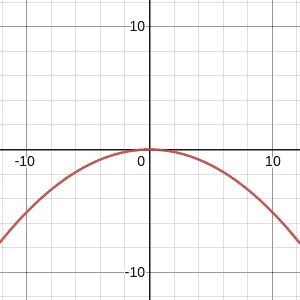
Along the x-axis is the velocity of the ball and the y-axis represents the height of the ball. At the centre, at v=0, this shows the maximum height of the ball – we just discussed that the ball stops (v=0) at the very top of its path, when gravitational potential energy is at its maximum.
As we increase or decrease the energy in the system, we can see that the maximum height of the ball increases and decreases!
This article has been co-authored by Cameron Bunney.