Why Do Hot Things Glow? An In-Depth Explanation
When we warn people not to touch an object that’s really hot, we might say something like “be careful! It’s red hot!”. We naturally associate color with everyday descriptions of hot things. There’s also a good reason for this – physically, hot objects tend to glow. But why?
Hot objects glow because the wavelength of thermal radiation emitted by the object shifts into the visible part of the spectrum as its temperature increases. In fact, all objects give off thermal radiation, but an object will only glow visibly if its temperature is high enough (approximately 798 K).
In this article, we’ll learn and understand the physical reasons for why hot things tend to glow. We’ll also learn the quantum mechanical processes that allow atoms to emit light.
Most importantly, we’ll be looking at the concept of black body radiation, which specifically helps us understand the relation between temperature and the “visible glow” coming from a hot object.
We’ll discover why objects have different colors at different temperatures and find out about the Draper point – the temperature above which all solid objects begin to visibly glow!
Table of Contents
How Atoms Emit Light According To Quantum Mechanics
Everything is made out of fundamental particles – quarks, electrons, photons, neutrinos etc. These are all governed by the rules of quantum mechanics. That which we consider to be “stuff” is when these fundamental particles interact and stay together: atoms.
To understand how any object can glow, we first need to understand how light is emitted at the atomic level.
An atom, at a fundamental level, can be considered as a positively charged nucleus made of protons and neutrons (themselves made out of quarks) and surrounded by a cloud of negatively charged electrons.
The important part of the atom for us is the cloud of electrons. These electrons each have their own energy, but the key difference in a quantum treatment as opposed to a classical one is that the electrons have discrete energy levels, usually denoted En.
Mathematically, there are an infinite amount of energy levels but we can give each one its own label – E1, E2 and so on.
The energy levels being discrete means you won’t find an electron with an energy in between E1 and E2. We say that the energy levels are quantized.
Interestingly, if electrons did not have these quantized energy levels, the electrons would actually end up spiraling into the nucleus and all atoms in the universe would be unstable – the world we know would not exist. If you want to know more about why this does NOT happen and what quantization of energy has to do with it, consider reading this article.
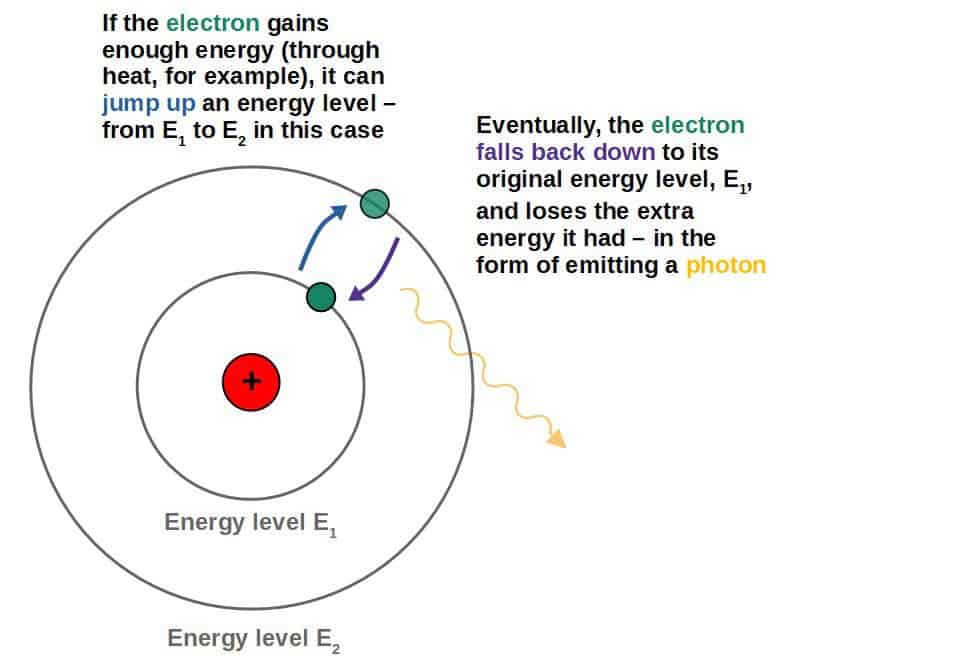
Now, if you heat something up, you give it energy. In the case of an atom, this extra energy can cause the electrons to jump to a higher energy level. We say that the electrons have been excited.
However, nature is inherently lazy and everything wants to exist in the lowest energy state that it can, so after a short period, the electrons will fall back to a lower energy state from their excited state.
Energy cannot be destroyed, so where does this energy go? It gets emitted from the atom in the form of photons!
The energy of a photon can be described by the following formula:
E=h\nuE here stands for the energy, h is Planck’s constant and ν is the frequency of the light (photon).
We can relate the frequency of the light emitted to its wavelength λ by:
\lambda=\frac{c}{\nu}Let’s say that an electron is in an excited state E2 and it falls back to its ground state E1. Then we can combine this to find the wavelength of the emitted light:
E=\frac{hc}{\lambda}\ \ \Rightarrow\ \ \lambda_{21}=\frac{hc}{E_2-E_1}So, from a purely quantum mechanical perspective for individual atoms, we can get an idea of how atoms give off light when heated – electrons get excited and emit photons.
Of course, all everyday objects are made of atoms, so this is the basic mechanism – though not the only one – by which an object will emit light and thus, glow, if the wavelength of the emitted light is in the visible range.
However, in many cases, the light emitted will not be in the visible part of the electromagnetic spectrum and this result also does not show the temperature dependence of the emitted light that we’re specifically after.
The other issue is that everyday objects are not just individual atoms but huge collections of atoms and molecules that interact in complicated ways. These collections of atoms tend to behave differently than just single atoms.
Even though the emission of light is at its heart, a quantum mechanical phenomenon, there is much more to the story – only explaining what happens at the atomic level is not sufficient.
The key to understanding why large, everyday objects (comprised of many atoms) glow when heated comes from understanding something called black body radiation.
We can essentially think of black body radiation as a statistical model that can describe how large-scale objects emit light and how temperature relates to it.
Black Body Radiation & Why Things Glow When Heated
First of all, any object with a temperature above absolute zero will give off so-called thermal radiation. This means effectively every object in the universe since even the vacuum of space is warmer than absolute zero.
Now, thermal radiation is simply what we call electromagnetic radiation (i.e. photons) when this radiation is caused by something being heated. So, thermal radiation is just electromagnetic radiation resulting from a temperature of above absolute zero.
So if everything is giving off thermal radiation, why don’t we see it?
Generally, thermal radiation will be given off at all possible wavelengths of electromagnetic radiation and visible light is only a small portion of this.
So, for most objects, we won’t be able to see any kind of visible glow coming from thermal radiation.
However, we do know that if an object is heated hot enough, it will begin to glow. So, what determines when the thermal radiation emitted by an object is visible and how does its temperature relate to this?
Well, one way to understand this is by looking at the black body radiation model in detail.
What Is Black Body Radiation?
For a start, black body radiation assumes that an object is a black body, an idealized object with uniform temperature and which only absorbs light (and doesn’t reflect it).
The thermal radiation given off by a black body is then called black body radiation.
Whilst not true black bodies, stars and many other objects can be approximated as such, so this is a fairly good model for understanding our question at hand – why do hot things glow?
Now, why do we want to look at black body radiation? Well, the main reason is that thermal radiation is an incredibly complicated phenomenon in general – here are a few reasons why:
- When an object is heated, there are so many atoms in an object of everyday size that predicting how each atom gets excited and emits photons through the quantum mechanical process discussed earlier is unpractical.
- Moreover, when an object is heated, the molecular structures inside the object themselves vibrate, which also causes thermal radiation (photons) to be emitted. This means that thermal radiation is also affected by the composition of a object.
- The point being here is that there are actually multiple mechanisms behind thermal radiation – while individual atoms only emit light through electrons jumping between energy states, in objects comprised of many many atoms, the emission of thermal radiation is much more complicated and the distribution of thermal radiation is going to be difficult to predict.
The nice thing about black body radiation is that since it’s an idealization, we can actually predict the thermal radiation coming from a black body (i.e. black body radiation) incredibly accurately.
The other nice thing is that this works as a great approximation for many objects in the real world as well.
In fact, we can describe the whole spectrum of thermal radiation of a black body and the colors of light resulting from this by a fairly simple function (which we’ll look at soon).
The most important result of the black body radiation model in our context is going to be the fact that the whole thermal radiation spectrum of a black body is completely determined by the temperature of the body, not for example, its composition or molecular structure.
Moreover, for each black body radiation spectrum, there is going to be a single prominent wavelength and most of electromagnetic radiation given off by the body is in this particular wavelength.
So, the temperature of a black body will determine what the wavelength of most of the electromagnetic radiation emitted by that body will be. If this wavelength is in the visible range (about 380nm-750nm), the body will emit visible light – and thus, appear glowing!
Now, for everyday things with relatively low temperatures such as people and houses, this wavelength is not in the visible part of the electromagnetic spectrum (and these aren’t perfect black bodies either).
This is to be expected, of course – you typically don’t see people just glowing red or blue walking down the street.
However, at certain high enough temperatures, the prominent wavelength will indeed be in the visible light range and objects will glow at different colors.
Moreover, there is actually a temperature at which if you heat any object up to, it will begin to glow visibly – yes, any object! This is called the Draper point, which we’ll discuss later in this article.
But first, let’s dive deeper into the concept of black body radiation and specifically, how we model it.
Planck’s Law
I’ll first go through the main model we use to describe black body radiation and then we can see how this brings about the prominent wavelengths, allowing us to understand why certain objects glow visibly when heated and others do not.
Black body radiation is characterized by Planck’s law:
B\left(\lambda{,}T\right)=\frac{2hc^2}{\lambda^5}\frac{1}{e^{\frac{hc}{\lambda k_BT}}-1}We can recognize h from before, Planck’s constant, c is the speed of light, and kB is the Boltzmann constant. The Boltzmann constant is most commonly seen in the study of thermodynamics but a perhaps more familiar place that it can be found is in the ideal gas law, PV=kBNT.
Planck’s law describes the spectral radiance B(λ,T) as a function of both the temperature of the black body (T) and the wavelength of emitted electromagnetic radiation (λ).
The spectral radiance is a quantity with the peculiar units of power per unit area per unit solid angle per unit wavelength.
Intuitively, it represents the energy flux (how much is passing through a unit surface) along a line of radiation in a certain direction.
Now, while the spectral radiance is a two-variable function, we can treat it as a function of only the wavelength λ by choosing a fixed temperature T for the body.
We can then represent the spectral radiance curves, B(λ), by plotting them as functions of the wavelength for bodies of different temperatures:
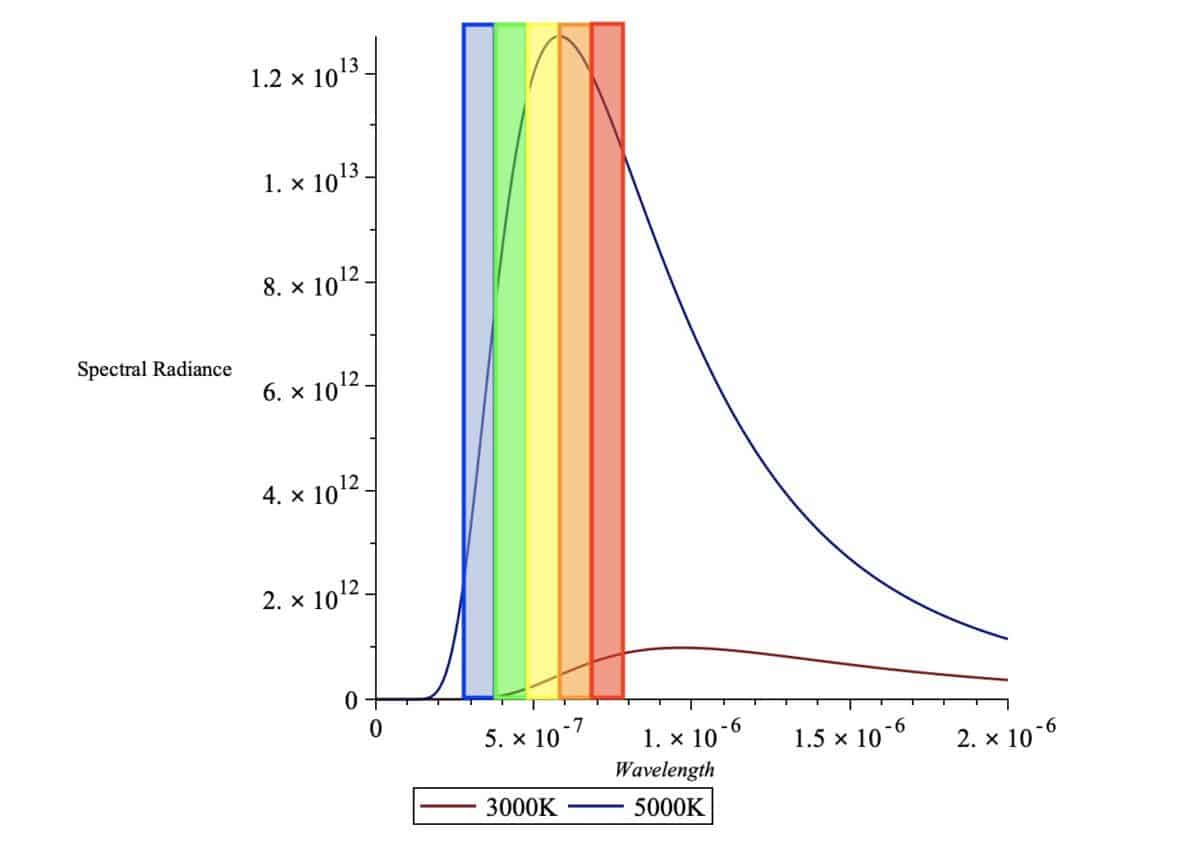
Here I’ve compared the spectral radiance of two black bodies at two different temperatures, 5000K and 3000K. I’ve overlaid the visible spectrum of light (380nm-750nm) along with the respective general colors.
But what does this graph tell us? The graph is a distribution of the energy of all the photons released by the black body.
Remember that the energy of a photon is related to either its wavelength or frequency as we saw before, so we can interpret the horizontal wavelength-axis here as representing energy as well!
So, if a point on the graph is higher than another (meaning the spectral radiance is higher), there are more photons being released with that energy (and that wavelength) and hence that particular color will be more prominent.
As we can see, both of the graphs have a maximum height at a point we call the peak wavelength. Most of the photons radiated by the body will be of this peak wavelength, which means that this particular wavelength and color will be the most prominent when actually looking at the body.
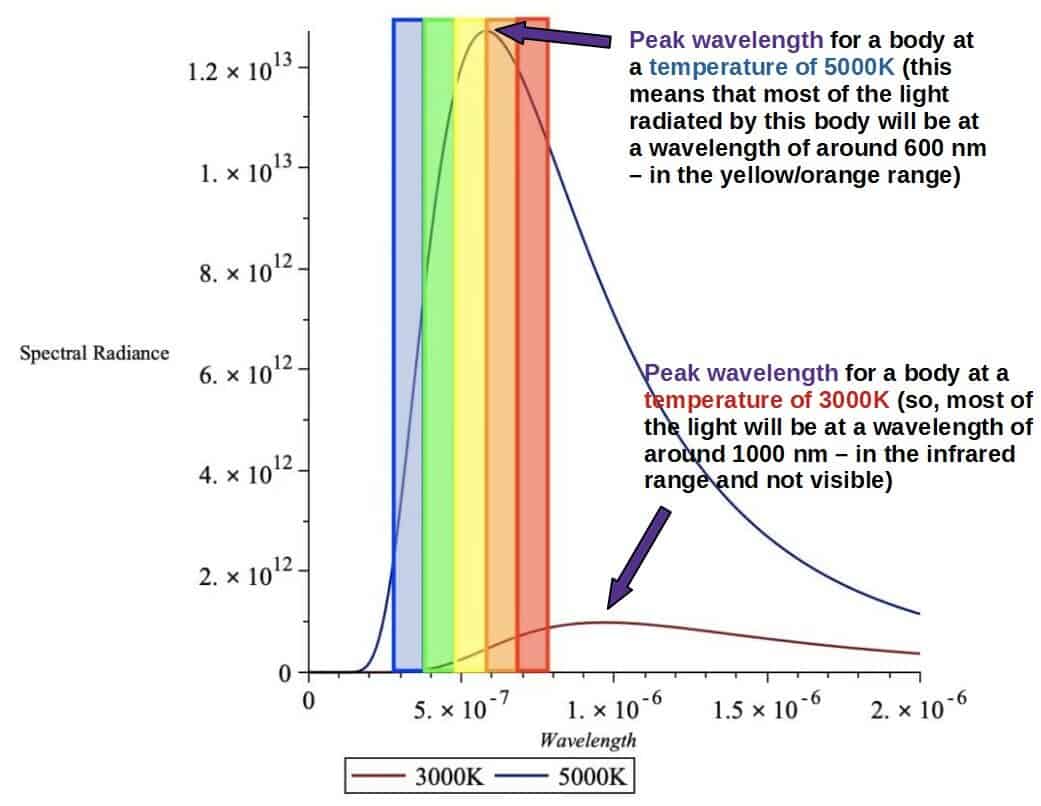
The surface of the Sun is around 5000K and from the graph above, the peak wavelength falls in the orange/yellow part of the visible spectrum – this is why the Sun appears mostly yellow to us!
However, this also brings us to a larger question – is there a way to relate the temperature of a body directly to the color of the light it emits?
Sure, here we can clearly see the color and the peak wavelength from the graph, but would it be possible to, for example, find an expression for the peak wavelength (and thus, the color) as a function of temperature?
It turns out that it is indeed possible and this result is known as Wien’s displacement law.
How Does Temperature Affect Color?
The color of a glowing object is determined by its temperature as described by Wien’s displacement law, which states that the wavelength of light emitted by an object is inversely proportional to its temperature. Therefore, hotter objects glow blue while cooler objects glow more red and yellow.
Now, the peak wavelength for any given black body can be written down as a very simple function of temperature:
\lambda_{peak}=\frac{\alpha}{T}The α here is a constant of proportionality with a value around 2.898×10-3 m*K. This inverse proportionality law is called Wien’s displacement law.
I’ll note first that each of the black body curves, with each curve determined by the temperature T, has only one maximum height (and no minimum).
Generally, we can find maxima (and minima) by differentiating any function and setting its derivative equal to zero. We can do the same for our spectral radiance function B(λ) from earlier (by again, treating the temperature T as a fixed value):
B\left(\lambda\right)=\frac{2hc^2}{\lambda^5}\frac{1}{e^{hc/\lambda k_BT}-1}The next step is to take a derivative of this with respect to the wavelength λ:
\frac{dB\left(\lambda\right)}{d\lambda}=2hc^2\left(-\frac{5}{\lambda^6}\frac{1}{e^{hc/\lambda k_BT}-1}-\frac{1}{\lambda^5}\frac{\left(-hc\right)}{\lambda^2k_BT}\frac{e^{hc/\lambda k_BT}}{\left(e^{hc/\lambda k_BT}-1\right)^2}\right) \frac{dB\left(\lambda\right)}{d\lambda}=\ \frac{2hc^2}{\lambda^7\left(e^{hc/\lambda k_BT}-1\right)^2}\left(\frac{hc}{k_BT}\cdot e^{hc/\lambda k_BT}-5\lambda\left(e^{hc/\lambda k_BT}-1\right)\right)This looks messy but it’s just an awkward application of the chain and product rules multiple times and then factoring things out to make life easier! Then we set this all to zero.
The prefactor in front of the parentheses here cannot equal zero so we just need to set what is inside the bracket equal to zero. We then get the following equation (note that the λ we get by solving this equation is going to be the peak wavelength λpeak):
\frac{hc}{k_BT}\cdot e^{\frac{hc}{\lambda_{peak}k_BT}}-5\lambda_{peak}\left(e^{\frac{hc}{\lambda_{peak}k_BT}}-1\right)=0To simplify things, we’ll use a substitution so we can see the clear structure of the equation. First, divide by λpeak and then let y=hc/λpeakkBT, so that we are then trying to solve the equation:
ye^y-5\left(e^y-1\right)=0While this may seem like an impossible equation to solve for y from and granted, this does not have a solution in terms of any simple elementary functions, we can actually solve this with the aid of the Lambert W function.
The Lambert W function is a somewhat weird and unordinary function, but it is incredibly useful in many cases. Essentially, the Lambert W function can be thought of as the inverse function to the function y(x)=xex.
So, if you were to act on this function with the Lambert W function, you’d get back the variable x here:
W\left(y\right)=W\left(xe^x\right)\ \ \Rightarrow\ \ x=W\left(y\right)The Lambert W is, however, technically, not a function since it is multivalued and it has multiple “branches”. If our x is a real variable, then we can represent W(x) with two different curves, called the W0 branch and the W-1 branch.
We can then graph these together to get an idea of what the “function” W(x) would look like:
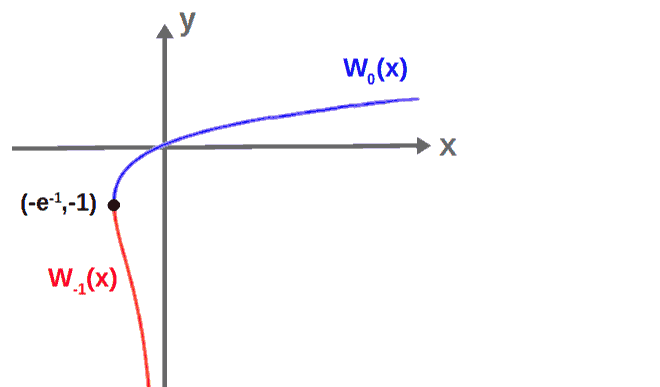
Now, since y>0 in our above equation yey-5(ey-1)=0, the principal branch, W0, is all we need. For an equation of the form wew=a, we would have w=W0(a) defined as the solution to the equation.
Our equation we want to solve is almost of this exact form. Let’s rewrite it again by first writing it as:
ye^y-5\left(e^y-1\right)=0\ \ \Rightarrow\ \ \left(y-5\right)e^y=-5Then, if make a second substitution y=x+5, we find:
\left(x+5-5\right)e^{x+5}=-5\ \ \Rightarrow\ \ xe^x=-5e^{-5}This is the defining equation of the Lambert W function with w=x and a=-5e-5. This tells us that the solution, the value of x, is given by:
x=W_0\left(-5e^{-5}\right)The value of W0 at this point, -5e-5, is approximately -0.03489.
Substituting back y=x+5 and also y=hc/λpeakkBT (which was our original definition for y) gives us the final solution for the peak wavelength:
\frac{hc}{\lambda_{peak}k_BT}=W_0\left(-5e^{-5}\right)+5\ \ \Rightarrow\ \ \lambda_{peak}=\frac{hc}{k_B\left(5+W_0\left(-5e^{-5}\right)\right)}\frac{1}{T}The coefficient here in front of 1/T is just a number with a value of ≈2.898×10-3 m*K. If we call this constant α, we then get Wien’s displacement law λpeak=α/T.
From Wien’s displacement law, we can see that as the temperature of a body increases, the peak wavelength of the radiation it emits, decreases.
Look back at the black body radiation graphs I plotted earlier. You can see that indeed, as we increase the temperature from 3000K to 5000K, the location of the peak moves slightly to the left – just as Wien’s displacement law predicts!
Since the peak wavelength represents the wavelength of the majority of the electromagnetic radiation the body is giving off and therefore, also determines the main color of the body, we observe that as things get hotter, their glowing color gets bluer.
If you look at the flame produced by a candle or a lighter, the hotter bottom part closest to the source is blue and the “cooler” part on the edge is more of a red color.

Wien’s displacement law helps us see exactly why that happens!
Below, I’ve included a table of the relationship between the temperature of an object and its main glowing color. These can be computed directly from Wien’s displacement law.
| Temperature | Glow Color |
|---|---|
| 4200 K (≈3900 °C) | Red |
| 4800 K (≈4500 °C) | Orange |
| 5000 K (≈4700 °C) | Yellow |
| 5300 K (≈5000 °C) | Green |
| 6400 K (≈6100 °C) | Blue |
| 7300 K (≈7000 °C) | Violet |
Note, however, that these values only apply to a black body. As stated earlier, not all objects are black bodies (no object is really a perfect black body), but many can be approximated as such.
Therefore, the values given above are only approximations and rough ranges.
Moreover, these only describe the colors of the peak wavelength of the light the object emits. Even though the peak wavelength is the most prominent one and thus, will determine the main color, the object will also emit some light at different wavelengths and colors.
At What Temperature Does Something Begin To Visibly Glow?
We have now seen why hot things glow but we could also ask what “hot” even means in this case – at what temperature does something actually start to glow visibly?
A first rough estimate could be obtained from Wien’s displacement law by noting the fact that the longest wavelength of visible light is around 750 nm.
This will therefore give the lowest possible temperature at which an object still emits visible light. If we rearrange Wien’s displacement law for the temperature instead and plug 750 nm as the peak wavelength, we get:
T=\frac{\alpha}{\lambda_{peak}}=\frac{\left(2.898\times10^{-3}\right)}{\left(7.5\times10^{-7}\right)}\approx3900KThis is what a naïve application of Wien’s displacement law would tell us – but we can experience many things glowing with temperatures much lower than 3900K. So what went wrong?
What we have neglected here is the fact that we do not necessarily need a peak wavelength that is in the visible part of the spectrum!
All our application of Wien’s displacement law has told us is that at a temperature of 3900K, most of the photons released will be visibly red.
However, a human eye is able to detect a surprisingly small amount of photons and therefore, we do not actually need most of the photons to be in the visible range.
In order to see something glow, we just need a small fraction of the photons to be in the visible range.
This means we can have a peak wavelength at much longer than 750nm and still observe a faint glow – in this case, the vast majority of the photons will be in the infrared category, however, some will still be in the visible spectrum and if we were in a dark room, we’d still be able to see a faint glow!
If 3900K is too high, then what actually is the minimum temperature that an object begins to glow at when heated?
This question was experimentally answered by John Draper, who established that all objects will begin to glow at a common, minimum temperature if heated. This temperature is now known as the Draper point.
The Draper point is at approximately 798 K or 525 °C. This is the temperature above which any object will begin to glow visibly at a faint red color if heated.
Cameron Bunney
I’m a third year PhD student at University of Nottingham, where I also studied my MMath. My main research focus is on curved spacetime QFT and the Unruh effect in analogue gravity systems. I have a soft spot for all kinds of math and physics, from number theory to mathematical biology and everything in between! Aside from research and recreational math, I enjoy playing piano and studying languages.
This article has been co-authored by Cameron Bunney.



