Constraints In Lagrangian Mechanics: A Complete Guide With Examples
In Lagrangian mechanics, while constraints are often not necessary, they may sometimes be useful. However, what do we actually mean by constraints in Lagrangian mechanics?
In Lagrangian mechanics, constraints are used to restrict the dynamics of a physical system. In the Lagrangian formulation, constraints can be used in two ways; either by choosing suitable generalized coordinates that implicitly satisfy the constraints, or by adding in additional Lagrange multipliers.
One of the most useful things about Lagrangian mechanics is that by a clever choice of generalized coordinates, we often do not need any constraint forces.
While this is completely valid for simply finding the equations of motion for a system, we may sometimes want to know the constraint forces as well.
For example, the tension in a string is a constraint force and calculating it may allow us to predict how much weight the string is able to hold before getting deformed.
In this article, we’ll be discussing all about what constraints are in Lagrangian mechanics, how they are used and lots of other things. We’ll also look at a bunch of different examples.
Now, just to give you an idea of what this article is about, there are generally two ways to use constraints in Lagrangian mechanics.
The first way is by using a so-called constraint equation to choose your generalized coordinates in a way that they implicitly contain all the information about the constraints.
This will give you the correct equations of motion, but it won’t give you information about the constraint forces.
The second way is by adding additional terms to the Euler-Lagrange equations that involve Lagrange multipliers. Doing this will give you the correct equations of motion as well as the constraint forces.
Before we get started, I’d highly recommend you check out my article Lagrangian Mechanics For Dummies, as everything discussed in this article will be based on the concepts explained there. If you’re really serious on learning Lagrangian mechanics, you’ll definitely enjoy my full book on the topic -more information can be found here.
You may also find this article helpful that is on the topic of generalized coordinates, how to choose them and apply them in practice. A lot of tools described in this article are going to be adding to the ideas discussed there.
Table of Contents
What Are Constraints and Constraint Forces?
Constraint forces are physical forces that make all objects in a given system obey the constraints specified for that system. For example, the normal force acting on a box sliding down a ramp is a constraint force that constrains the box to remain on the ramp and not fall through it.
In other words, constraint forces are needed to make sure that a given physical system behaves in exactly the way it should, such as an object not falling through the ground even though gravity is pulling it that way.
In Newtonian mechanics, we pretty much always have to add in these constraint forces when using Newton’s second law, F=ma, to make sure that the constraints in a system are obeyed.
However, the clever thing about Lagrangian mechanics is that we can choose any coordinate system we wish to describe a given system and these are called generalized coordinates.
We can therefore often choose our coordinates in a way that they implicitly contain all the constraints already and there is no need to introduce any constraint forces anymore; the constraints are already encoded in our choice of generalized coordinates.
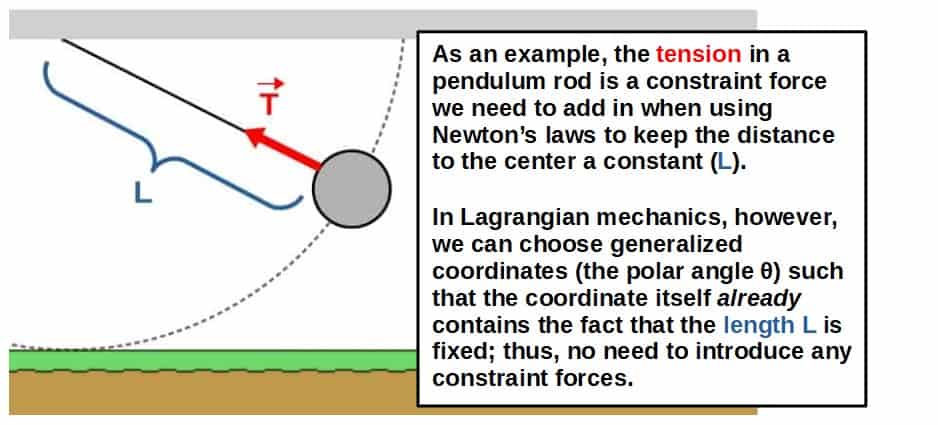
You can read more about generalized coordinates and how to choose and use them in practice from this article that also shows you some examples of this.
Below I’ve also added an example of how using these constraint forces works in Newtonian mechanics. This will help illustrate better how generalized coordinates can then be used to avoid the use of constraint forces altogether.
Let’s look at how the constraint force, the tension in the pendulum example, actually works in Newtonian mechanics.
In particular, let’s construct Newton’s second law (F=ma) in both the radial direction as well as in the tangential direction:
\sum_{ }^{ }F_r=ma_r\\\sum_{ }^{ }F_t=ma_tThe forces in the radial direction are the tension force (which acts completely in the radial direction) and the radial component of gravity and the only force in the tangential direction is the tangential component of gravity (picture of these below).
Now, here’s the important thing; the tension and the radial component of gravity have to be equal and opposite in order for the distance L to be constant.
This is why we have to add in this tension force in the first place; to constrain the pendulum to move in such a way that the length L is fixed and in practice, we do this by “balancing” out the forces such that this constraint is obeyed.
Now, we can find the radial and tangential forces by placing the pendulum in an xy-coordinate system and specifying the angle θ, which can be used to split the force of gravity into its radial and tangential components:
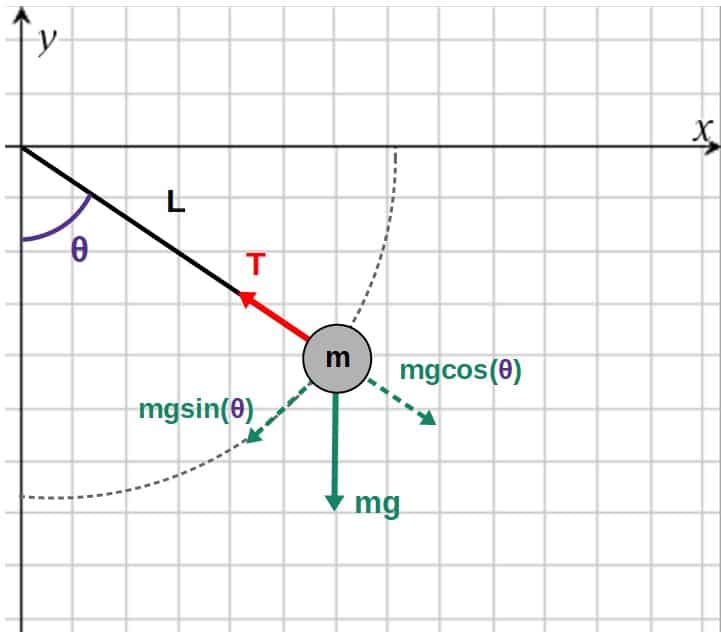
The net forces in the radial and tangential directions are then:
\sum_{ }^{ }F_r=-T+mg\cos\theta\\\sum_{ }^{ }F_t=-mg\sin\thetaOn the right-hand side of Newton’s second law, we need to use the components of the acceleration in polar coordinates:
a_r=\ddot r-r\dot{\theta}^2\\a_t=r\ddot \theta+2\dot r\dot \thetaThese dots are used to denote time derivatives. So, for example r with two dots would be d2r/dt2 (the acceleration of the “radial” coordinate).
We then get from Newton’s second law:
mg\cos\theta-T=m\left(\ddot{r}-r\dot{\theta}^2\right)\\-mg\sin\theta=m\left(r\ddot \theta+2\dot r\dot \theta\right)So far, however, we haven’t our constraint at all in our equations. We’ll do this now.
We know that the distance to the origin (the coordinate r) should be fixed as r=L (this is our “constraint equation”), which means that its time derivatives must be zero:
\dot{r}=0{,}\ \ddot r=0The equations of motion from Newton’s second law are then:
mg\cos\theta-T=-mL\dot{\theta}^2\\-mg\sin\theta=mL\ddot{\theta}We can write these as:
T=mL\dot{\theta}^2+mg\cos\theta \ddot{\theta}=-\frac{g}{L}\sin\thetaThe second equation is just the equation of motion for the θ-coordinate, which in principle, can be solve to find θ(t).
The first equation, however, tells you what the tension force has to be in order for the length of the rod to stay constant.
Hopefully this illustrates the general process of using constraints in Newtonian mechanics; we add in these constraint forces and then determine what these forces have to be in order for the constraints to be satisfied.
Constraint Equations
In Lagrangian mechanics, constraints can be implicitly encoded into the generalized coordinates of a system by so-called constraint equations.
In mechanics, constraint equations are equations that relate the coordinates describing a given system to the constraints that the system must obey. Constraint equations can be used to find relations between coordinates and simplify the choice of generalized coordinates.
We usually want to write these constraint equations as a function of the coordinates (qi‘s) set equal to zero (this is actually called a holonomic constraint; I’ll explain what this means later):
f\left(q_1{,}q_2{,}q_3...\right)=0This can always be done for any equation by just moving every term to one side. We’ll see why this is useful a bit later.
Some examples of these constraint equations might be a particle constrained to move on a sphere, in which case it must satisfy the relation (R is the radius of the sphere):
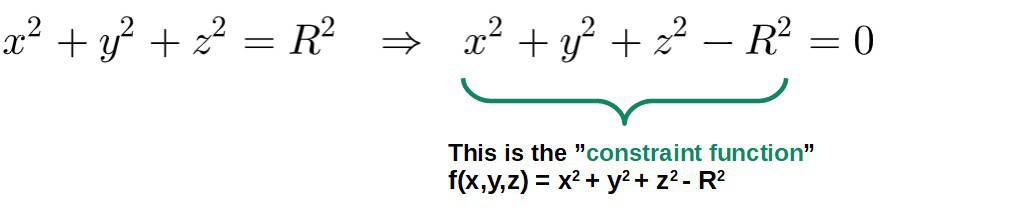
Now, what do you actually do with these constraint equations?
Well, simply put, these are equations you can use to simplify your choice of generalized coordinates for the system. If you use the constraint equations cleverly, you may be able to choose your generalized coordinates in such a way that they implicitly contain all the constraints.
You could then use these cleverly chosen generalized coordinates to find the equations of motion for the system, which will automatically obey the constraints.
The way to do this is quite straightforward; if you have a constraint equation that relates the coordinates in some way, you can use that equation to express one of the coordinates in terms of the others.
In other words, you can eliminate one of the coordinates using the constraint equation, which will make sure that the constraint is then implicitly encoded into your description of the system. You’ll find an example of this below.
Let’s go back to the pendulum example again. Before we did it using Newtonian mechanics. This time, we’ll do it using Lagrangian mechanics and this method of using constraint equations when choosing generalized coordinates.
What we’ll discover is that we get the right equations of motion without needing to introduce any constraint forces.
To get started, let’s again place the pendulum in an xy-coordinate system with the angle θ (a function of time) being the angle between the pendulum rod and the y-axis. The mass is again m and the length of the rod is L.
Now, instead of adding in a bunch of forces, let’s just express the x- and y- coordinates of the pendulum using polar coordinates, r and θ (the radial distance from the center and the angle to the vertical):
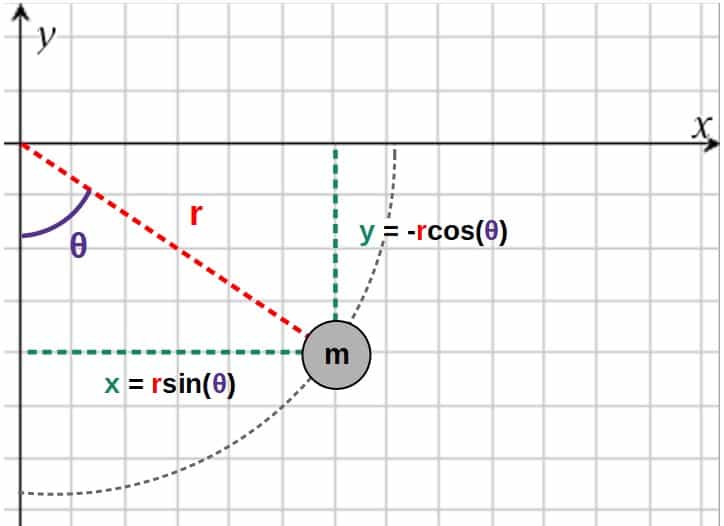
Now, let’s write down our constraint equation. We know that at all times, the length of the rod should be a constant L, which means that the radial distance r must be equal to this. Our constraint equation can then be expressed as:
r=LIf you want, you can write this in the form f(r)=0, where f(r)=r-L. This form will be useful later when we introduce Lagrange multipliers.
Anyway, we now have a constraint equation we can use to eliminate one of our coordinates, namely the r-coordinate. Using this constraint (r=L), the xy-coordinates of the pendulum bob become:
x=r\sin\theta\ \ \Rightarrow\ \ x=L\sin\theta\\y=-r\cos\theta\ \ \Rightarrow\ \ y=-L\cos\thetaThe nice thing is that we’ve now eliminated the r-coordinate completely and we have the coordinates of the pendulum expressed in terms of one generalized coordinate, θ.
But even better, this choice of generalized coordinates is now also consistent with the constraint (the length of the rod must be L). Thus, the equations of motion we get will also obey the constraint.
Let’s then construct the Lagrangian. If we take the time derivatives of our x,y-coordinates, we get:
\dot{x}=L\dot \theta\cos\theta\\\dot{y}=L\dot{\theta}\sin\thetaThe kinetic energy will then be:
T=\frac{1}{2}m\left(\dot{x}^2+\dot{y}^2\right)=\frac{1}{2}mL^2\dot \theta^2The potential energy of the pendulum bob will just be V=mgh, where the height h will be the y-coordinate (if we choose the “zero-level” of the potential to be at y=0):
V=mgh=-mgL\cos\thetaSo, our Lagrangian is:
L=T-V=\frac{1}{2}mL^2\dot{\theta}^2+mgL\cos\thetaWe can get the equations of motion from the Euler-Lagrange equation for the θ-coordinate:
\frac{d}{dt}\frac{\partial L}{\partial\dot{\theta}}-\frac{\partial L}{\partial\theta}=0Inserting the Lagrangian, we have:
\frac{d}{dt}\left(mL^2\dot{\theta}\right)-\left(-mgL\sin\theta\right)=0\\\Rightarrow\ \ mL^2\ddot{\theta}+mgL\sin\theta=0\\\Rightarrow\ \ \ddot{\theta}=-\frac{g}{L}\sin\thetaThis, of course, is the same thing we had with Newton’s laws.
The beautiful thing about this, however, is that we were able to obtain the correct equation of motion (which obeys the constraints) simply by choosing our generalized coordinates such that they implicitly contain the constraints.
This then allowed us to find the equation of motion without ever needing to introduce any constraint forces (the tension).
Now, this method of using the constraint equations when choosing the generalized coordinates for a system is one way to include constraints in Lagrangian mechanics.
This method works great if you only care about finding the correct equations of motion, but not necessarily about the constraint forces themselves.
This method will completely eliminate the need for any constraint forces, so you won’t be able to get information about those this way.
You’ll simply get the correct equations of motion WITHOUT needing to introduce any constraint forces, which is often what we want in order to describe the system.
However, we CAN also include the constraint forces into the Lagrangian formulation if we want to. This is explained later, but first we need to discuss the different types of constraints that are possible.
In case you're interested, I have a FREE downloadable PDF (that you'll find here) that covers a bunch of applications of Lagrangian mechanics, such as deriving the elliptical orbits of planets, proving Kepler's laws and a lot more.
Types of Constraints In Classical Mechanics (Holonomic vs Non-Holonomic)
It’s possible to have different types of constraints for dynamical systems in classical mechanics, but what exactly are these different types of constraints?
There are two types of constraints in classical mechanics: holonomic constraints and non-holonomic constraints. Holonomic constraints are constraints that can be written as an equality between coordinates and time. Any constraint that cannot be expressed this way is a non-holonomic constraint.
An example of a holonomic constraint would be a particle moving in a circle, in which case it would have the following constraint:
x^2+y^2=R^2This is the type of constraint we saw previously with the pendulum as well. These holonomic constraints are always expressed as equalities involving the coordinates (and possibly time as well), however, NOT the velocities.
Moreover, holonomic constrains are sometimes categorized into two “sub-types”, scleronomic (the constraint equations do not explicitly depend on time) and rheonomic (the constraint equations do explicitly depend on time) constraints.
An example of a non-holonomic constraint, on the other hand, would be a particle allowed to move inside a circle, in which case it would have the following constraint:
x^2+y^2\le R^2So, non-holonomic constraints can be inequalities, for example.
Also, any constraint that involves the velocities or differentials of the coordinates (but cannot be integrated to obtain the “full constraint equation” that involves the coordinates themselves) is a non-holonomic constraint.
You’ll find an example of where such a constraint comes up in the case of describing the physics of a unicycle.
The motion of a unicycle is a classic example of where non-holonomic constraints show up in the form of constraints for the velocities.
Let’s place the unicycle in an x,y,z -coordinate system, so as it moves, its position is going to be described by some coordinates (x,y,z).
Now, the special thing about a unicycle is that it can also have an “orientation”, meaning that at any point, the unicycle can be pointed in a different direction. We’ll label this orientation by an angle θ:
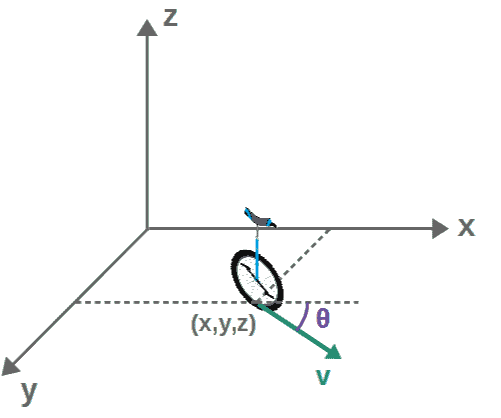
If the unicycle is not allowed to “jump” up and down, we have z=0, which reduces the degrees of freedom to just three; the position coordinates x and y as well as the orientation θ (these are our generalized coordinates, which change with time, i.e. they are all functions of time).
However, while the angle θ can point to any direction at different points (meaning that there is no straightforward relation or constraint between θ, x and y), the components of the velocity cannot just be anything.
This is because the direction of the velocity v is determined by the orientation of the unicycle, in other words, by the angle θ. Thus, the components of the velocity (time derivatives of x and y) are given by:
\dot{x}=v\cos\theta\\\dot{y}=v\sin\thetaIf we divide the second equation by the first, we get:
\frac{\dot{y}}{\dot{x}}=\frac{\sin\theta}{\cos\theta}\ \ \Rightarrow\ \ \dot y=\dot x\tan\thetaHere we basically have a constraint for the velocities. This is an example of a non-holonomic constraint, since it can be expressed in the form of a function of velocities (and coordinates):
f\left(\theta{,}\ \dot{x}{,}\ \dot{y}\right)=0\ {,}\ \ f\left(\theta{,}\ \dot{x}{,}\ \dot{y}\right)=\dot{y}-\dot{x}\tan\thetaNow, the thing about such a constraint is that it cannot be used to reduce the degrees of freedom in the system (i.e. solve for one of the coordinates in terms of the others), since we cannot write this in the form of a function of the coordinates only.
You can certainly try to express the above non-holonomic constraint in terms of the coordinates only by integrating both sides with respect to time, for example:
\dot{y}=\dot{x}\tan\theta\ \ \Rightarrow\ \ y=\int_{ }^{ }\dot{x}\tan\theta dtThe problem here is that both x-dot and θ are independent functions of time. We therefore cannot do the integral on the right-hand side and thus, we cannot get a relation between the coordinates from this.
This is one of the key points about non-holonomic constraints; they do not allow us to reduce the degrees of freedom even though they technically do constrain the system in some way.
Now, the situation would change if the angle θ is assumed to NOT depend on time (i.e. the angle θ is just some constant θ0, meaning that the unicycle cannot turn in another direction).
In this case, we could integrate the constraint to get:
y=\int_{ }^{ }\dot{x}\tan\theta_0dt=\tan\theta_0\int_{ }^{ }dx=x\tan\theta_0Note that I’ve set the integration constants to zero here.
So, we do get a relation between the coordinates here, namely that y=xtan(θ0), so actually, our constraint here turns into a holonomic constraint and the system would therefore only need one generalized coordinate, the coordinate x (since by knowing x, we automatically know y also).
For the rest of the article, we’ll only be discussing holonomic constraints as these are the most common types of constraints and also the most useful ones, generally speaking.

How To Find Constraint Forces In Lagrangian Mechanics (Step-By-Step Method)
So far, we’ve only discussed how to implicitly encode constraints into the generalized coordinates describing a system and how doing this leads to the correct equations of motion that obey the constraints.
However, doing it this way does not actually give you the constraint forces themselves.
So, if we wanted to find the actual constraint forces, what would we do in that case? This is what we’ll discuss next.
First of all, here is the rough step-by-step process of how constraint forces can be found in Lagrangian mechanics:
- Define the constraints by writing down a constraint equation for each constraint.
- Define a set of generalized coordinates without applying the constraints yet.
- Write down the Lagrangian (again, with no constraints applied).
- Apply the modified Euler-Lagrange equations with constraints and Lagrange multipliers.
- You should now have the equations of motion for each coordinate with Lagrange multipliers.
- Solve for the Lagrange multipliers, which will give you the constraint forces.
Essentially, the most important part in this process is #2 and the fact that we do NOT use the constraints yet when first defining our generalized coordinates.
This is kind of a “trick” to give us unconstrained equations of motion and we will then apply the constraints later. Doing it this way allows us to actually find the constraint forces (this will become clear later when we look at various examples).
Now, the constraints themselves are defined by the constraint equations, which we discussed before.
These are equations that set relationships between the coordinates and we write these equations, generally, in the form:
f\left(q_1{,}q_2{,}q_3{,}...\right)=0It’s important to write the equation in this form (which you can always do by simply moving everything to one side), because this gives you the correct constraint function, f.
Also, note that when using this method, we have to use the so-called modified Euler-Lagrange equations, which introduce these new variables called Lagrange multipliers.
It is exactly the Lagrange multipliers that will give us the constraint forces.
Before we discuss Lagrange multipliers, however, let’s first discuss the modifications we need to add to the Euler-Lagrange equations in order to find constraint forces.
The Euler-Lagrange Equation With Constraints
Simply put, the Euler-Lagrange equation with constraints has the following form:
\frac{d}{dt}\frac{\partial L}{\partial\dot{q}_i}-\frac{\partial L}{\partial q_i}=\sum_j^{ }\lambda_j\frac{\partial f_j}{\partial q_i}Let’s look at what each of these things here mean:
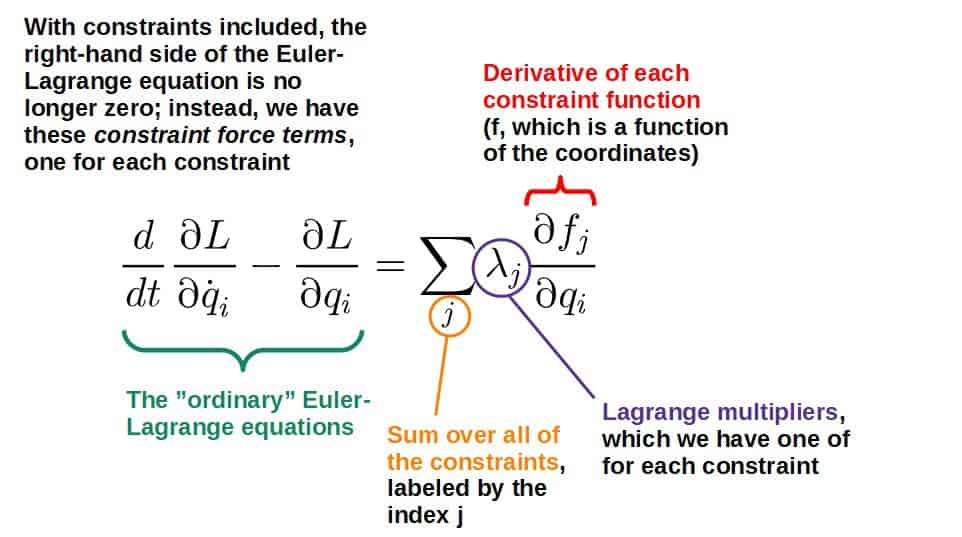
Intuitively, the right-hand side here represents the constraint forces (a sum over all them), so these Lagrange multipliers will give you information about how the constraint forces behave.
In practice, when we write down the unconstrained Lagrangian, we will essentially get “additional” equations of motion (which would not be there if we choose our generalized coordinates to implicitly contain the constraints).
We can then use these “additional” equations of motion to solve for the Lagrange multipliers and find the constraint forces that way (you’ll find an example of this below).
So, we’re basically adding in extra degrees of freedom by introducing these Lagrange multipliers, but since we get these “additional” unconstrained equations of motion, we also have more equations.
I cover the Euler-Lagrange equation and the intuition behind what it actually means in this article. In there, I also discuss the notion of generalized forces (which is what you see on the right-hand side in the modified Euler-Lagrange equation).
For a more mathematical discussion of the Euler-Lagrange equation, I recommend also reading this complete guide to calculus of variations.
Let’s consider the pendulum example again. Earlier, we found the following relations between the polar coordinates (r,θ) and the Cartesian coordinates (x,y) of the pendulum bob:
x=r\sin\theta\ {,}\ \ y=-r\cos\thetaWe the used our constraint equation (r=L) to essentially “eliminate” the r-coordinate completely and only describe the system with the θ-coordinate.
We won’t do that now. Instead, we’ll construct the “unconstrained” Lagrangian for this system (meaning that the radial distance, the r-coordinate is allowed to vary, for now). We’ll then use our constraints later.
If we take the time derivatives of these “unconstrained” x- and y-coordinates, we get (note that r is now also a function of time, so we have to use the product rule):
\dot{x}=\dot{r}\sin\theta+r\dot{\theta}\cos\theta\\\dot y=-\dot{r}\cos\theta+r\dot{\theta}\sin\thetaWe can then get the kinetic energy by squaring these. I’ll skip a little bit of the algebra here, but what you’ll get (after cancelling terms and using cos2θ+sin2θ=1) is the following:
T=\frac{1}{2}m\left(\dot{x}^2+\dot{y}^2\right)=\frac{1}{2}m\left(\dot r^2+r^2\dot \theta^2\right)The potential energy is going to be V=mgy, so:
V=-mgr\cos\thetaOur “unconstrained” Lagrangian is then:
L=T-V=\frac{1}{2}m\left(\dot{r}^2+r^2\dot{\theta}^2\right)+mgr\cos\thetaNotice that we basically have two coordinates here, r and θ, so we’ll get an Euler-Lagrange equation for each of them. We also have to use the modified Euler-Lagrange equations here with the added stuff on the right-hand side:
\frac{d}{dt}\frac{\partial L}{\partial\dot{q}_i}-\frac{\partial L}{\partial q_i}=\sum_j^{ }\lambda_j\frac{\partial f_j}{\partial q_i}In our case, we only have one constraint, so this sum over j has just one term (I’ll call these λ1=λ and f1=f). For the r-coordinate, we have:
\frac{d}{dt}\frac{\partial L}{\partial\dot{r}}-\frac{\partial L}{\partial r}=\lambda\frac{\partial f}{\partial r}Let’s now recall what our constraint equation was for the pendulum: r=L. Therefore, we can write this constraint in terms of the constraint function as:
f\left(r\right)=0\ {,}\ \ f\left(r\right)=r-LThe partial derivative of this, ∂f/∂r, is then just 1. So, the Euler-Lagrange equation becomes:
\frac{d}{dt}\frac{\partial L}{\partial\dot{r}}-\frac{\partial L}{\partial r}=\lambda\frac{\partial f}{\partial r}\ \ \Rightarrow\ \ \frac{d}{dt}\frac{\partial L}{\partial\dot{r}}-\frac{\partial L}{\partial r}=\lambdaBy inserting the Lagrangian, we get the equation of motion for the r-coordinate:
\frac{d}{dt}\left(m\dot{r}\right)-\frac{\partial}{\partial r}\left(\frac{1}{2}m\left(\dot{r}^2+r^2\dot{\theta}^2\right)+mgr\cos\theta\right)=\lambda\\\Rightarrow\ \ m\ddot{r}-mr\dot{\theta}^2-mg\cos\theta=\lambda\\\Rightarrow\ \ \ddot{r}=\frac{\lambda}{m}+r\dot{\theta}^2+g\cos\thetaLet’s then look at the Euler-Lagrange equation for θ:
\frac{d}{dt}\frac{\partial L}{\partial\dot{\theta}}-\frac{\partial L}{\partial\theta}=\lambda\frac{\partial f}{\partial\theta}The right-hand side here goes to zero, since our constraint function f does not depend on θ (so ∂f/∂θ=0). We then have:
\frac{d}{dt}\frac{\partial L}{\partial\dot{\theta}}-\frac{\partial L}{\partial\theta}=0\\\Rightarrow\ \ \frac{d}{dt}\left(mr^2\dot{\theta}\right)-\frac{\partial}{\partial\theta}\left(\frac{1}{2}m\left(\dot{r}^2+r^2\dot{\theta}^2\right)+mgr\cos\theta\right)=0Note that we have to use the product rule on the time derivative (first term). Also, when taking the time derivative of r2, we have to use the chain rule (so, dr2/dt=2rdr/dt).
\Rightarrow\ \ 2mr\dot{r}\dot{\theta}+mr^2\ddot{\theta}+mgr\sin\theta=0\\\Rightarrow\ \ \ddot{\theta}=-\frac{g}{r}\sin\theta-\frac{2}{r}\dot{r}\dot{\theta}Notice what we have now. We have two unconstrained equations of motion:
\ddot{r}=\frac{\lambda}{m}+r\dot{\theta}^2+g\cos\theta \ddot{\theta}=-\frac{g}{r}\sin\theta-\frac{2}{r}\dot{r}\dot{\theta}We’ve essentially obtained the unconstrained equations of motion in order to get this additional equation for the Lagrange multiplier λ. We can NOW apply our constraint (r=L), which means that:
\dot r=0\ {,}\ \ \ddot r=0Our equations of motion will then become:
0=\frac{\lambda}{m}+L\dot{\theta}^2+g\cos\theta \ddot{\theta}=-\frac{g}{L}\sin\thetaDo you see what just happened? We first obtained the unconstrained equations of motion and after that, we applied our constraint. This results in the right equation of motion (the one for θ), but we also got an additional equation that we can now solve for λ:
\lambda=-mL\dot{\theta}^2-mg\cos\thetaIf you now look at the expression we found for the tension force using Newton’s laws earlier, it is exactly this (apart from a minus sign, which we get here because the tension is “opposing” the radial direction), so:
T=\lambda=-mL\dot{\theta}^2-mg\cos\thetaThis hopefully illustrates the process of finding constraint forces in Lagrangian mechanics as well as how the Lagrange multipliers describe these constraint forces.
Again, I want to stress that this method only works because we first find the unconstrained equations of motion. Only by doing this will we get enough equations to solve for the constraint forces (Lagrange multipliers).
On the other hand, if you apply the constraints before finding the equations of motion, you’ll only obtain the equations of motion themselves (which are perfectly correct if these are the only thing you wish to find), but not expressions for the actual constraint forces.
The example above might give you an idea of how Lagrange multipliers describe the constraint forces, but let’s discuss this more next.
We’ll also look at the intuition behind where these Lagrange multipliers and the modified Euler-Lagrange equations actually come from (and connect these ideas to an area of math known as constrained optimization).
As a sidenote, you may also find this article interesting, which shows you how friction and non-conservative forces can be dealt with in Lagrangian mechanics. I also show you examples, such as a pendulum with air resistance.
Lagrange Multipliers & How To Use Them
Lagrange multipliers, as we saw earlier, are these coefficients we add to the Euler-Lagrange equations that we can then solve for. But what do they actually represent?
In mechanics, Lagrange multipliers contain information about the constraint forces in a given system. This can be understood by the fact that the Lagrange multipliers appear in additional generalized force terms in the equations of motion and physically, these correspond to the constraint forces.
There is, however, an extremely important point to note here; the Lagrange multipliers themselves are NOT the actual, physical constraint forces.
Yes, they do contain information about the constraint forces but by themselves, they are not the constraint forces. I’ll explain this in more detail soon.
First, to actually understand where the Lagrange multipliers and all these things come from, we need to discuss some ideas from constrained optimization.
You’ll find this below (and a geometric explanation behind the Lagrange multipliers).
To really get a nice geometric picture of where these Lagrange multipliers actually originate from, we need to look at an area of math called constrained optimization.
Essentially, this is just multivariable calculus with the goal of optimizing (finding minima or maxima) a multivariable function under a certain constraint.
So, imagine we have some function g(x,y) that we want to optimize. This could, for example, be a function that describes the profit a business makes, based on some variables x and y, so we would want to maximize this function.
But, we also have a certain constraint, described by a constraint function f(x,y). This could be, for example, a certain limited budget for the business (don’t worry, we’ll connect these ideas to physics very soon). The actual constraint would be given mathematically by an equation of the form:
f\left(x{,}y\right)=0We then want to optimize (find the maximum of g(x,y)), such that it obeys the constraint f(x,y)=0. How could this be done?
The way to geometrically understand this is that both of the functions, g(x,y) and f(x,y), describe surfaces if we place them in a Cartesian coordinate system.
Now, let’s say we have a particular value k of the function g(x,y). In other words, g(x,y)=k is some curve on the graph of g(x,y), called a contour line. But, our constraint f(x,y)=0 is also a contour line, namely the curve where the value of f(x,y) is zero, i.e. the curve along which the constraint is satisfied.
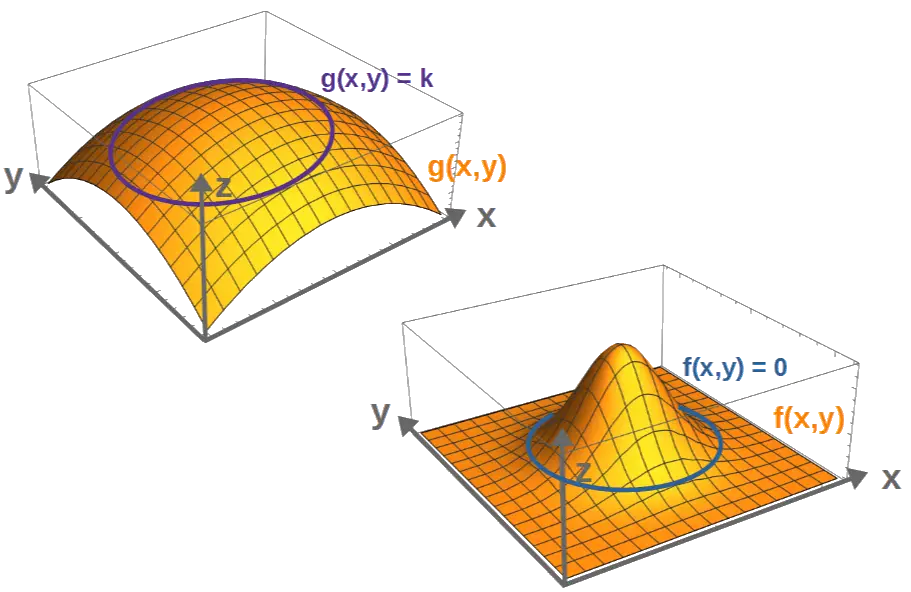
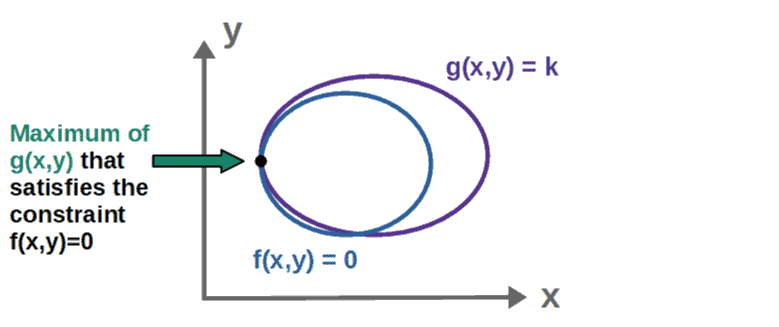
In order for k to be a maximum of g(x,y) such that the constraint f(x,y)=0 is also satisfied, we must have two things; first, the contour lines g(x,y)=k and f(x,y)=0 must meet in order for g(x,y)=k to satisfy the constraint.
Secondly, for k to specifically be a maximum of g(x,y), the contour lines g(x,y)=k and f(x,y)=0 must be tangent to one another (i.e. they must go in the same direction at that point).
In case you’re familiar with stuff about vector calculus, you’ll know that the gradient of a scalar function always points perpendicular to these contour lines (for more on vector calculus, I recommend checking out my Vector Calculus For Physics: A Complete Self-Study Course).
Now, because at this maximum point, the contour lines are tangent to one another (they are going in the same direction at this point), therefore also the gradient vectors at this must point in the same direction.
In other words, the gradients at this point are proportional to one another (when we say that two vectors are “proportional” to one another, it just means that they point in the same direction):
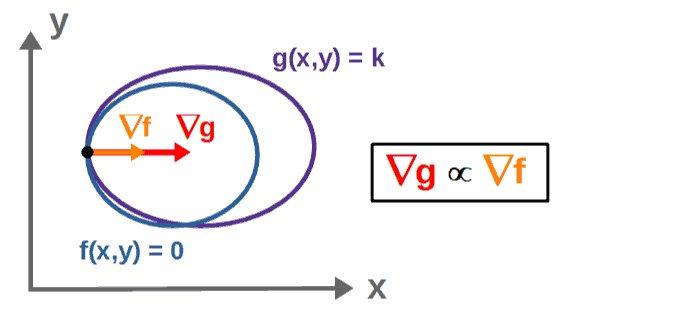
An equivalent way of stating this would be that we can express these gradient vectors as multiples of one another by adding in a proportionality constant (we’ll call it λ):
\nabla g=\lambda\nabla fThe maximum points (x,y) of g(x,y) under the constraint f(x,y)=0 are then the solutions to this equation (which gives you one equation for each component of the gradients, so two equations in this case).
Now, an important thing to realize here is that normally (when there aren’t any constraints), if we want to find the minima or maxima of a function g(x,y), we would solve the equation:
\nabla g=0However, when we require that these minima and maxima also obey some constraint f(x,y)=0, then the right-hand side is no longer zero, but instead contains this λ∇f-term (understanding this is important for the physical interpretation we’ll discuss soon).
This proportionality constant λ here is exactly the Lagrange multiplier and geometrically, it tells you how much the gradients are pointing in the same direction, i.e. how much the function g changes (this is what ∇g describes) due to a small change in f, the constraint (a small change in f being described by ∇f).
So, if the Lagrange multiplier λ is very large, then by changing the constraint just a small amount will cause a big change in the maximum or minimum of the function g that is to be optimized.
Also, if the Lagrange multiplier happens to be zero, we can interpret this as saying that a change in the constraint does not affect the minima or maxima of g. This may be easier to interpret soon when we connect all of this to physics.
Now, basically the same idea applies in physics and Lagrangian mechanics.
To understand this, let’s think about what the function we want to optimize is; it is the Lagrangian, since the principle of least action tells you that all objects follow trajectories such that, at each point in time, the Lagrangian is at a minimum (or stationary point).
So really, what we want to do is to minimize the Lagrangian under a set of constraints. This would give the equations of motion that obey the constraints we subject the system to.
However, the Lagrangian is a much more complicated function than just some multivariable function g(x,y) and to understand how the Lagrangian is minimized under constraints, let’s first think about how the Lagrangian (or the action, more accurately) is minimized when there are no constraints.
With no constraints, the condition that the action is minimized is that the Lagrangian obey the Euler-Lagrange equations, i.e. a set of derivatives with the right-hand side being set to zero:
\frac{d}{dt}\frac{\partial L}{\partial\dot{q}_i}-\frac{\partial L}{\partial q_i}=0This is roughly speaking, analogous to the fact that we minimize an “ordinary” multivariable function by setting its gradient (∇g, which is a bunch of partial derivatives just like the Euler-Lagrange equation) equal to zero.
Now, analogously to when a multivariable function is minimized under constraints, the right-hand side of the “minimum condition” (∇g=0) is no longer zero but now contains these Lagrange multipliers (λ∇f), the same happens when minimizing the action under constraints; we add in Lagrange multipliers and the “gradient” (partial derivatives) of the constraint function:
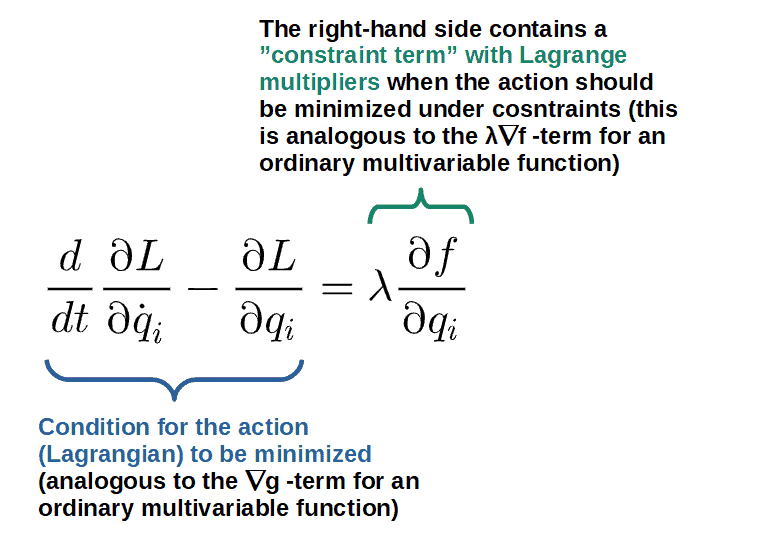
Now, making this analogy between the constrained Euler-Lagrange equation and the constraint equation in multivariable calculus (∇g=λ∇f), we also gain a very nice physical interpretation of the Lagrange multipliers.
Namely, since the Lagrange multipliers tell you how much the “function to be optimized” changes when the constraint is changed, then physically, the Lagrange multiplier tells us how much the action (or the Lagrangian) changes with a small change in the constraint.
But what exactly does this tell us physically? Well, since the constraint function is only a function of position and not velocity (assuming holonomic constraints), changing it would result in a change in the Lagrangian in the form of a change in the potential energy.
So, if the constraint changes and as a result, the potential energy changes, then there must be a force that would change the system’s potential energy by the constraint changing; this is the constraint force.
This then gives the interpretation of the Lagrange multipliers as being closely related to the constraint forces.
Now, this is kind of an ad hoc -way of coming to this conclusion and it’s really not exact, but the intuitive idea is quite nice as it is only a result of the geometric interpretation of the Lagrange multipliers. We’ll look at this in a more accurate manner soon.
How Are Lagrange Multipliers Related To Constraint Forces?
To get back to the point mentioned earlier, Lagrange multipliers by themselves are generally speaking, not the actual constraint forces.
In fact, by themselves, they are just some parameters that may or may not make any physical sense.
However, the actual constraint forces are given by the generalized force term in the modified Euler-Lagrange equations:
Q_i=\sum_j^{ }\lambda_j\frac{\partial f_j}{\partial q_i}In other words, we have to find the Lagrange multipliers first and then “combine” them with this partial derivative of the constraint function -term and this will give you the constraint forces.
For each coordinate qi, this Qi will give you the component of the total constraint force in the direction of the coordinate qi, which may or may not be zero.
As an example (which you’ll find more of later), consider the Lagrange multiplier we found for the pendulum system earlier:
\lambda=-mL\dot{\theta}^2-mg\cos\thetaThe constraint forces for the pendulum (in both the r- and θ-directions) would then be:
Q_r=\lambda\frac{\partial f}{\partial r}=\lambda=-mL\dot{\theta}^2-mg\cos\theta Q_{\theta}=\lambda\frac{\partial f}{\partial\theta}=0As a reminder, the constraint function here was f=r-R.
So, in this case, the Lagrange multiplier is indeed exactly the constraint force but generally it’s not going to be; only if it is combined with this partial derivative -term will it give you the real constraint force.
The notion of Lagrange multipliers fundamentally comes from the mathematics of constrained optimization, which we discussed previously.
We concluded that the Euler-Lagrange equations should get modified to the following form if we have a constraint given by an equation f=0:
\frac{d}{dt}\frac{\partial L}{\partial\dot{q}_i}-\frac{\partial L}{\partial q_i}=\lambda\frac{\partial f}{\partial q_i}However, an equivalent way of obtaining this form of the Euler-Lagrange equations is by defining a “new” Lagrangian of the form:
L'=L+\lambda fThe clever thing about this is that, actually, this “new” Lagrangian is exactly the same as the old one, given that the constraints are satisfied (i.e. f=0, in which case L’=L). So, we’re just trivially adding zero to the Lagrangian and thus, we’re not really changing any of the dynamics of the system.
Now, if we apply the Euler-Lagrange equations to this, we end up with the same modified Euler-Lagrange equation:
\frac{d}{dt}\frac{\partial L'}{\partial\dot{q}_i}-\frac{\partial L'}{\partial q_i}=0\\\Rightarrow\ \ \frac{d}{dt}\frac{\partial}{\partial\dot{q}_i}\left(L+\lambda f\right)-\frac{\partial}{\partial q_i}\left(L+\lambda f\right)=0\\\Rightarrow\ \ \frac{d}{dt}\frac{\partial L}{\partial\dot{q}_i}-\frac{\partial L}{\partial q_i}-\lambda\frac{\partial f}{\partial q_i}=0An important point here is that this only works for holonomic constraints (constraints that are not velocity-dependent). Otherwise the velocity-derivative of f would not be zero and we wouldn’t end up with the right equation.
Now, even though we essentially aren’t changing the Lagrangian at all, we still get these new force terms:
Q_i=\lambda\frac{\partial f}{\partial q_i}This is because, generally, the “position” derivative terms in the Euler-Lagrange equation describe forces of some sorts. Another way to see this would be to interpret the “new” Lagrangian as:
L'=L+\lambda f=T-U\ {,}\ \ U=V-\lambda fSo, we could, in a sense, interpret this λf -term as a potential since it only depends on position (again, this is sort of trivial since f=0).
We could then say that the “total force”, let’s call it Fi, is given by the gradient (derivative with respect to the position coordinates, qi) of this:
F_i=-\frac{\partial U}{\partial q_i}=-\frac{\partial V}{\partial q_i}+\lambda\frac{\partial f}{\partial q_i}And, as you may guess, this new force term resulting from the constraint f is exactly the constraint force (which doesn’t do any work on the system, so it physically doesn’t really change anything important).
Now, this constraint force term may not be zero even if the constraint function f itself is. The elegance of this method is that we’re practically not changing our Lagrangian at all (by only adding zero to it), yet these constraint forces just somehow happen to drop out of our equations.
We can understand this by the fact that the constraint forces cannot do work, so they don’t change the system’s energy at all. We can see this by looking at an “infinitesimal” work done (δW) by these constraint forces (Qi) if we displace all our coordinates qi by some small amount δqi:
\delta W=\sum_i^{ }Q_i\delta q_i=\sum_i^{ }\lambda\frac{\partial f}{\partial q_i}\delta q_iThis thing here with the sum over the partial derivatives and the displacements is just the total change in f (δf). Now, if we assume that the constraint is satisfied at all times, then the equation f=0 (a constant) must hold and the “total change” in a constant is always zero:
\delta W=\lambda\delta f=0Indeed, the constraint forces do no work. They are just kind of there, but since they don’t affect the energy of the system in any way, they don’t really do anything to the actual dynamics and so, adding them in doesn’t affect anything.
In other words, we’ve just added constraint forces into our description in a way that is completely consistent with everything; you don’t have to add them in (you can work only with properly chosen generalized coordinates if you don’t want to deal with constraint forces), but you can.
The nice thing, however, is that we get these λ’s in the Euler-Lagrange equations, which we can solve for. Then, after solving for these, we can compute the constraint forces by:
Q_i=\lambda\frac{\partial f}{\partial q_i}Examples of Constraints In Lagrangian Mechanics
In this section, we’ll look at some practical examples of using constraints and finding constraint forces in Lagrangian mechanics.
If you want to see more examples of how Lagrangian mechanics is applied and used in practice (such as in the study of the orbital dynamics of planets), I have a free downloadable PDF that you’ll find on this page.
Particle Moving on a Spiral
This example essentially consists of finding the equations of motion and the constraint forces for a particle moving on a spiral trajectory.
Mathematically, we can describe a spiral in polar coordinates by saying that the radius increases linearly with the angle (this is called an Archimedean spiral). So, in polar coordinates, the spiral is described by the following curve:
r\left(\theta\right)=a\thetaThis a here is some proportionality constant with units of lengths. The trajectory of the particle then looks more or less as follows:
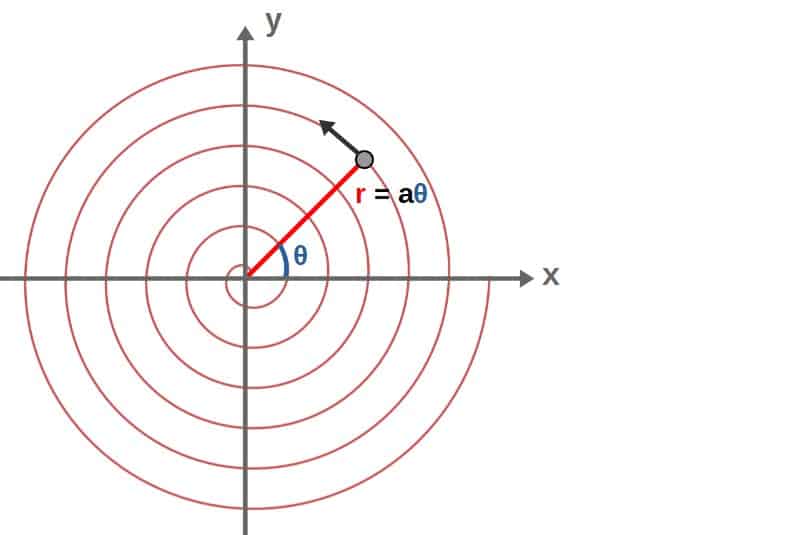
You’ll find the full detailed solution to this down below.
The Lagrangian for the particle just consists of the kinetic energy, since there is no potential in this case. We can write it in standard polar coordinates as:
L=\frac{1}{2}m\left(\dot{r}^2+r^2\dot{\theta}^2\right)Note that I haven’t used the constraint at all yet, so this would be the Lagrangian for a freely moving particle. Our constraint function, in this case, can be obtained from the relation r=aθ, so:
f\left(r{,}\theta\right)=r-a\theta=0For this system, we’ll have two equations of motion, one for the r-coordinate and one for θ. Later on, when we apply our constraint, we can reduce these to just an equation of motion for θ as well as an expression for the constraint force.
Now, the equation of motion for r will be (note that we have only one constraint, so the “sum” on the right-hand side just involves one term with only one Lagrange multiplier):
\frac{d}{dt}\frac{\partial L}{\partial\dot{r}}-\frac{\partial L}{\partial r}=\lambda\frac{\partial f}{\partial r}\\\Rightarrow\ \ \frac{d}{dt}\left(m\dot{r}\right)-mr\dot \theta^2=\lambda\\\Rightarrow\ \ \ddot{r}=\frac{\lambda}{m}+r\dot{\theta}^2On the other hand, the equation of motion for θ will be:
\frac{d}{dt}\frac{\partial L}{\partial\dot{\theta}}-\frac{\partial L}{\partial\theta}=\lambda\frac{\partial f}{\partial\theta}\\\Rightarrow\ \ \frac{d}{dt}\left(mr^2\dot{\theta}\right)=\lambda\left(-a\right)\\\Rightarrow\ \ 2mr\dot{r}\dot{\theta}+mr^2\frac{d\dot{\theta}}{dt}=-a\lambda\\\Rightarrow\ \ \ddot{\theta}=-\frac{a\lambda}{mr^2}-\frac{2}{r}\dot{r}\dot{\theta}So, we have the following two unconstrained equations of motion:
\ddot{r}=\frac{\lambda}{m}+r\dot{\theta}^2 \ddot{\theta}=-\frac{a\lambda}{mr^2}-\frac{2}{r}\dot{r}\dot{\theta}We will now apply the constraint r=aθ, which means that:
\dot{r}=a\dot{\theta}\ {,}\ \ \ddot{r}=a\ddot{\theta}So, using these and r=aθ, we have from the first equation of motion (for the r-coordinate):
a\ddot{\theta}=\frac{\lambda}{m}+a\theta\dot{\theta}^2\ \ \Rightarrow\ \ \ddot{\theta}=\frac{\lambda}{ma}+\theta\dot{\theta}^2And for the second one:
\ddot{\theta}=-\frac{\lambda}{ma\theta^2}-\frac{2}{\theta}\dot{\theta}^2Now, these are both of course equal, so we have:
\frac{\lambda}{ma}+\theta\dot{\theta}^2=-\frac{\lambda}{ma\theta^2}-\frac{2}{\theta}\dot{\theta}^2We can solve this for the Lagrange multiplier λ:
\lambda=-\frac{2\theta+\theta^3}{1+\theta^2}ma\dot{\theta}^2Then, we can also insert this into either of the equations of motion for θ to obtain:
\ddot{\theta}=\frac{\lambda}{ma}+\theta\dot{\theta}^2\\\Rightarrow\ \ \ddot{\theta}=-\frac{2\theta+\theta^3}{1+\theta^2}\dot{\theta}^2+\theta\dot{\theta}^2\\\Rightarrow\ \ \ddot{\theta}=-\frac{\theta}{1+\theta^2}\dot{\theta}^2We then have the equation of motion for the particle as well as an expression for the Lagrange multiplier:
\ddot{\theta}=-\frac{\theta}{1+\theta^2}\dot{\theta}^2 \lambda=-\frac{2\theta+\theta^3}{1+\theta^2}ma\dot{\theta}^2The constraint forces the directions of both r and θ are then:
Q_r=\lambda\frac{\partial f}{\partial r}=-\frac{2\theta+\theta^3}{1+\theta^2}ma\dot{\theta}^2 Q_{\theta}=\lambda\frac{\partial f}{\partial\theta}=\frac{2\theta+\theta^3}{1+\theta^2}ma^2\dot{\theta}^2Particle Sliding Off a Sphere (with Lagrangian mechanics!)
The following example is basically a particle that begins sliding (initially from rest) down a half-sphere. At some point, it will slide off the sphere and we want to know exactly when the particle leaves the sphere.
In particular, we can describe the particle’s position by an angle θ (relative to the vertical). We therefore want to find the specific angle θ0 at which the particle falls off the sphere:
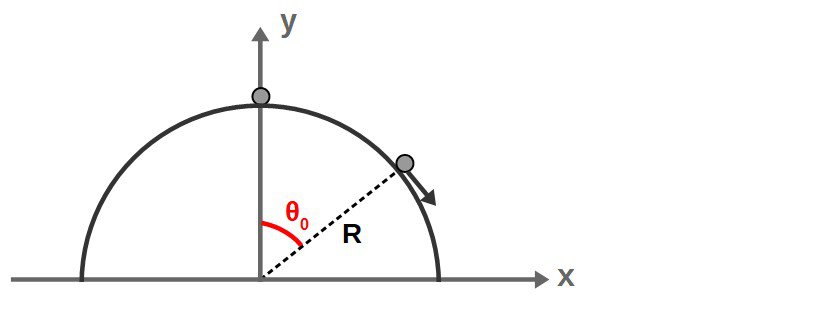
The way to solve this problem using Lagrangian mechanics is to find the constraint force (which corresponds to the normal force of the surface) and then look at when that normal force goes to zero, which will give you the angle at which the particle loses contact with the sphere.
This example also highlights an important application of the Lagrange multiplier method and that is to be able to not just find the constraint forces, but also analyze when these constraint forces may break down and not apply anymore.
This is because of the fact that in many systems (like our example here), the constraints will only apply up to a certain point or limit, after which they may no longer describe the dynamics of the system accurately and it’s often important to know when this happens.
The Lagrangian for this system is actually exactly the same as the Lagrangian for a pendulum, but with the potential energy having a different sign (this just comes from the fact that the height in V=mgh is now the +y-coordinate, instead of -y like we had with the pendulum earlier):
L=\frac{1}{2}m\left(\dot{r}^2+r^2\dot{\theta}^2\right)-mgr\cos\thetaAgain, this is the “unconstrained” Lagrangian, so we haven’t used any constraints yet here.
Our constraint for this system is that in the portion of the motion we care about, which is the part where the particle is ON the sphere still, the particle’s distance from the origin (r) is just the radius of the sphere (R), a constant. We can use this to get our constraint function:
r=R\ \ \Rightarrow\ \ f\left(r\right)=r-R=0Let’s now look at the equations of motion, which we have two of. First, the equation of motion for the r-coordinate gives us:
\frac{d}{dt}\frac{\partial L}{\partial\dot{r}}-\frac{\partial L}{\partial r}=\lambda\frac{\partial f}{\partial r}\\\Rightarrow\ \ \frac{d}{dt}\left(m\dot{r}\right)-\left(mr\dot{\theta}^2-mg\cos\theta\right)=\lambda\\\Rightarrow\ \ \ddot{r}=\frac{\lambda}{m}+r\dot{\theta}^2-g\cos\thetaFor the θ-coordinate, we have:
\frac{d}{dt}\frac{\partial L}{\partial\dot{\theta}}-\frac{\partial L}{\partial\theta}=\lambda\frac{\partial f}{\partial\theta}\\\Rightarrow\ \ \frac{d}{dt}\left(mr^2\dot{\theta}\right)-mgr\sin\theta=0\\\Rightarrow\ \ \frac{d}{dt}\left(r^2\dot{\theta}\right)=gr\sin\thetaIt’s useful for us to leave the time derivative in this form, as we’ll see soon. Now, these are the two unconstrained equations of motion. If we now use our constraint, r=R, we have:
\dot{r}=0\ {,}\ \ \ddot r=0With these, our equations of motion become:
0=\frac{\lambda}{m}+R\dot{\theta}^2-g\cos\theta\ \ \Rightarrow\ \ \dot{\theta}^2=\frac{g}{R}\cos\theta-\frac{\lambda}{mR} \frac{d}{dt}\left(R^2\dot{\theta}\right)=gR\sin\theta\ \ \Rightarrow\ \ \ddot{\theta}=\frac{g}{R}\sin\thetaNow, let’s take the time derivative of the first equation (note that we have to use the chain rule on the left-hand side and on the right, λ is generally a function of time):
\frac{d}{dt}\dot{\theta}^2=\frac{d}{dt}\left(\frac{g}{R}\cos\theta-\frac{\lambda}{mR}\right) \Rightarrow\ \ 2\ddot{\theta}\dot{\theta}=-\frac{g}{R}\dot{\theta}\sin\theta-\frac{\dot{\lambda}}{mR} \Rightarrow\ \ \left(2\ddot{\theta}+\frac{g}{R}\sin\theta\right)\dot{\theta}=-\frac{\dot{\lambda}}{mR}We now use our second equation (the equation for θ-double dot) and insert it into this one to get:
\left(2\frac{g}{R}\sin\theta+\frac{g}{R}\sin\theta\right)\dot{\theta}=-\frac{\dot{\lambda}}{mR}\ \ \Rightarrow\ \ \frac{3g}{R}\sin\theta\dot{\theta}=-\frac{\dot{\lambda}}{mR}We can now integrate both sides of this with respect to time to get:
\frac{3g}{R}\int_{ }^{ }\sin\theta\frac{d\theta}{dt}dt=-\frac{1}{mR}\int_{ }^{ }\frac{d\lambda}{dt}dt \Rightarrow\ \ \frac{3g}{R}\int_{ }^{ }\sin\theta d\theta=-\frac{1}{mR}\int_{ }^{ }d\lambda \Rightarrow\ \ -\frac{3g}{R}\cos\theta=-\frac{1}{mR}\lambda+C\ \ \ \ \ \ \left(1\right)Note that we also have to add in this integration constant C here. To figure out what this constant is, let’s go back to one of the equations from earlier:
\dot{\theta}^2=\frac{g}{R}\cos\theta-\frac{\lambda}{mR}If we assume that the particle starts from rest initially, then at t=0, we have both θ=0 and θ-dot=0, so this equation would be:
0=\frac{g}{R}\cos\left(0\right)-\frac{\lambda}{mR}\ \ \Rightarrow\ \ 0=\frac{g}{R}-\frac{\lambda}{mR}Now compare this to what happens for equation (1) from above at t=0 and θ=0:
-\frac{3g}{R}\cos\left(0\right)=-\frac{1}{mR}\lambda+C\ \ \Rightarrow\ \ 0=\frac{3g}{R}-\frac{\lambda}{mR}+CWe can see that in order for both of these equations to match at t=0 (which they should), we must have the terms not involving λ to be equal:
\frac{g}{R}=\frac{3g}{R}+C\ \ \Rightarrow\ \ C=-\frac{2g}{R}Okay, now let’s insert this result for C back into equation (1):
-\frac{3g}{R}\cos\theta=-\frac{1}{mR}\lambda+C\ \ \Rightarrow\ \ -\frac{3g}{R}\cos\theta=-\frac{1}{mR}\lambda-\frac{2g}{R}We’ve done a lot of math so far, but here comes the really important part; at the point when the particle leaves the surface of the sphere, the normal force due the surface must be zero.
Now, the normal force is just the constraint force in the radial direction and if this is to be zero, then we must have:
Q_r=\lambda\frac{\partial f}{\partial r}=\lambda=0At the point where λ, the θ-coordinate will have some value θ0, which is the angle we’re looking for, so our equation from above then becomes:
-\frac{3g}{R}\cos\theta=-\frac{1}{mR}\lambda-\frac{2g}{R}\\\Rightarrow\ \ -\frac{3g}{R}\cos\theta_0=-\frac{2g}{R}\\\Rightarrow\ \ \theta_0=\arccos\left(\frac{2}{3}\right)So, the particle falls off the sphere when the angle is at θ0=arccos(2/3), which is approximately θ0≈48°.