Why Do Electrons Not Fall Into The Nucleus? (or can they?)
If electrons are negatively charged and the nuclei in atoms are positively charged, they should attract each other and intuitively, it would seem that electrons should just fall into the nucleus.
However, since you’re reading this and you’re made out of stable atoms and so is every other object you see around you, there must be something else going on. So why exactly do electrons not fall into the nucleus?
Electrons obey the rules of quantum mechanics, according to which they can only have very specific energies and therefore cannot fall into the nucleus. However, there is nonetheless a small probability to find an electron inside the nucleus, which results in phenomena like electron capture.
In this article, we’ll discuss the classical picture of an electron and see why, according to the classical rules like Newton’s laws of motion, electrons should fall into the nucleus.
This creates a bit of a paradox, but we’ll then take a look at how quantum mechanics changes things and fixes this.
Also, this new quantum mechanical arena allows for more phenomena, such as an electron being found within and interacting with the nucleus, allowing effects such as electron capture.
Now, this article won’t be your typical pop-science content you’ll often find regarding this question. Instead, we’ll actually look at what our current understanding of physics and quantum mechanics really predicts and how this comes about from our mathematical models.
Table of Contents
Why Electrons Should Fall Into The Nucleus (According To Classical Mechanics)
Classical mechanics is what we used to describe physics previously, before quantum mechanics was developed. Everything in classical mechanics is governed by Newton’s laws (like F=ma).
According to classical mechanics, electrons should indeed fall into the nucleus. In fact, ALL electrons should and we should not have a single stable atom – but for more reasons than your intuition might tell you!
The original – classical – picture of an atom was of a ball-like electron orbiting the nucleus much like how the moon orbits the Earth.
Even if this orbiting-model were correct, the electron should still not just “fall” into the nucleus – it should keep orbiting, just like the Earth keeps orbiting the Sun and doesn’t just fall into it randomly.
However, something special happens because the electron has an electric charge. Because of its charge, any electron in this orbiting type of motion would inevitably fall into the nucleus. But why?
The answer can be found in classical electrodynamics and goes by a result called Larmor’s power formula – it describes the phenomenon that accelerating charges produce electromagnetic radiation.
Anything in orbital motion, including an electron orbiting around the nucleus, is accelerating.
This is because for the electron to remain in orbit, its velocity must at least change direction (and not just be a straight line) and therefore, there must be acceleration. The same thing happens when the Earth orbits the Sun – it is in accelerated motion in order to remain in orbit.
So, an electron orbiting the nucleus of an atom is accelerating and therefore also produces electromagnetic radiation.
Larmor’s power formula tells us how much radiation or more precisely, the power of electromagnetic radiation that is given away and this is given by the following formula:
P=\frac{2}{3}\frac{q^2a^2}{4\pi\varepsilon_0c^3}Here, q is the charge of the accelerating charged particle, a is its acceleration, c is the speed of light and ε0 is the “vacuum
permittivity” constant (a constant of nature that shows up a lot in electrodynamics).
Now, why is this important? Well, anything that is radiating will lose energy because it gives off radiation.
Power is directly related to energy as it is defined as the change in energy per unit time (mathematically, it is the time derivative of energy).
This is exactly what Larmor’s formula tells us – it describes the rate of change in the accelerating particle’s energy due to radiation.
This radiation is an overall loss of energy for the electron we’re considering, so the change in energy (power) will be negative. We write this as:
P=\frac{dE}{dt}=-\frac{2}{3}\frac{q^2a^2}{4\pi\varepsilon_0c^3}=-\frac{1}{6\pi\varepsilon_0c^3}e^2a^2Here we’ve set the charge q to be the charge of an electron, e, so that this formula now describes specifically the rate of change of an electron’s energy.
To describe how the orbit of the electron changes due to this loss of energy (and therefore, whether it will fall into the nucleus), we want to find an expression for the evolution of the orbit radius of the electron over time.
Using Newton’s laws, we can indeed do this and the result turns out to be (see below for the full derivation of this expression):
r\left(t\right)=\left(R_0^3-\frac{e^4}{4\pi^2\varepsilon_0^2m^2c^3}t\right)^{\frac{1}{3}}R0 here is the radial location of the electron (radius of the electron’s orbit) initially at time t = 0.
This is a somewhat complicated looking expression, but it describes the radius of the electron’s orbit as a function of time – how the radius changes with time due to radiative losses in energy.
To obtain the radius as a function of time, we want a differential equation that describes the evolution of the radius over time. We can begin by writing the time derivative of the radius via the chain rule as:
\frac{dr}{dt}=\frac{dE}{dt}\frac{dr}{dE}=\frac{dE}{dt}\frac{1}{\frac{dE}{dr}}We already have dE/dt from Larmor’s power formula so we just need a formula for the total energy in terms of the radius r.
As in classical mechanics, the total energy is given by kinetic energy plus potential energy. The potential for a point charge in electrodynamics is given by the Coulomb potential (V=-e2/4πε0r), so we have:
E=\frac{1}{2}mv^2-\frac{e^2}{4\pi\varepsilon_0r}The electron is in circular motion, which is defined by the following force equation (this comes from the fact that in a circular orbit, the Coulomb force F=e2/4πε0r2 is exactly balanced by the centrifugal force F=mv2/r):
\frac{mv^2}{r}=\frac{e^2}{4\pi\varepsilon_0r^2}We can rearrange this to find an expression for the kinetic energy in terms of the radius r (by multiplying both sides by r/2):
\frac{mv^2}{r}=\frac{e^2}{4\pi\varepsilon_0r^2}\ \ \Rightarrow\ \ \frac{1}{2}mv^2=\frac{e^2}{8\pi\varepsilon_0r}Then, inserting this into the expression for the total energy, we get:
E=\frac{e^2}{8\pi\varepsilon_0r}-\frac{e^2}{4\pi\varepsilon_0r}\ \ \Rightarrow\ \ E\left(r\right)=-\frac{e^2}{8\pi\varepsilon_0r}We now have an expression for the energy as a function of the radius r, which we can take the derivative of:
\frac{dE}{dr}=\frac{d}{dr}\left(-\frac{e^2}{8\pi\varepsilon_0r}\right)=\frac{e^2}{8\pi\varepsilon_0r^2}Now we can put this all together to find dr/dt:
\frac{dr}{dt}=\frac{dE}{dt}\frac{1}{\frac{dE}{dr}}=-\frac{e^2a^2}{6\pi\varepsilon_0c^3}\frac{8\pi\varepsilon_0r^2}{e^2}=-\frac{4}{3}\frac{r^2}{c^3}a^2We still need an equation for the acceleration! Luckily, Newton’s second law (F=ma) handles this for us – the force acting on the electron is given by the Coulomb force F=e2/4πε0r2, so we have:
\frac{e^2}{4\pi\varepsilon_0r^2}=ma\ \ \Rightarrow\ \ a=\frac{e^2}{4\pi\varepsilon_0mr^2}Here, m is the mass of the electron.
We can now insert this into the expression for dr/dt:
\frac{dr}{dt}=-\frac{4}{3}\frac{r^2}{c^3}a^2\ \ \Rightarrow\ \ \frac{dr}{dt}=-\frac{e^4}{12\pi^2\varepsilon_0^2m^2c^3}\frac{1}{r^2}To find r(t) from this, let’s move the r2 to the other side and multiply by dt:
r^2dr=-\frac{e^4}{12\pi^2\varepsilon_0^2m^2c^3}dtWe can now simply integrate both sides to get:
\int_{ }^{ }r^2dr=-\frac{e^4}{12\pi^2\varepsilon_0^2m^2c^3}\int_{ }^{ }dt\ \ \Rightarrow\ \ \frac{1}{3}r^3=-\frac{e^4}{12\pi^2\varepsilon_0^2m^2c^3}t+\frac{1}{3}R_0^3
Here, R0 corresponds to the radius at time t = 0, so I’ve defined the integration constant here as R03/3.
We can then solve this to find r(t) by simply multiplying by 3 and raising everything to the power 1/3:
r\left(t\right)=\left(R_0^3-\frac{e^4}{4\pi^2\varepsilon_0^2m^2c^3}t\right)^{\frac{1}{3}}The key point here is that the radius goes to zero when enough time has passed, in particular, when the time t reaches the value:
t=\frac{4\pi^2\varepsilon_0^2m^2c^3R_0^3}{e^4}This means that after enough time, the electron does indeed fall into the nucleus! Well, at least according to the rules of classical mechanics and classical electrodynamics, it does.
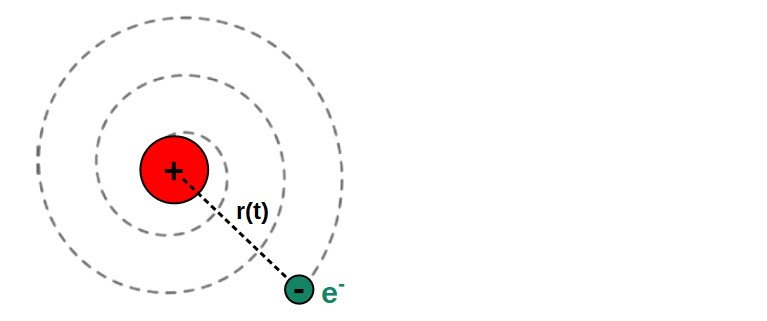
But empirically, we know that atoms are relatively stable and are not all falling apart with their electrons falling into the nucleus. So what is really happening?
Why Do Electrons Not Fall Into The Nucleus? (According To Quantum Mechanics)
This very question is what interested physicists before the quantum revolutions. Quantum mechanics was the missing ingredient.
The problem with the classical analysis we looked at is that an electron is not a classical particle – it is a quantum particle described by quantum mechanics, so the rules of classical mechanics do not necessarily apply to an electron.
Next, we’ll take a look at how quantum mechanics describes an electron and in particular, why quantum mechanics prevents an electron from simply falling into the nucleus.
One of the most powerful tools discovered during the development of quantum mechanics was the Schrödinger equation:
i\hbar\frac{\partial\psi\left(x{,}t\right)}{\partial t}=\left(-\frac{\hbar^2}{2m}\nabla^2+V\left(x{,}t\right)\right)\psi\left(x{,}t\right)The main object in this equation is the wave function ψ(x,t). This is a complex function and for an electron is related to the probability of finding the electron at a particular point in space and time.
The exact probability is given by squaring the absolute value of the wave function:
P=\left|\psi\left(x{,}t\right)\right|^2The point of the Schrödinger equation is to solve for the wave function, given a particular potential V(x,t).
The left-hand side of the Schrödinger equation tells us how the wave function changes with time. The i is the imaginary unit and ℏ is the reduced Planck’s constant that tells us that what we are dealing with is a quantum object.
On the right-hand side, we have a Hamiltonian term that is a result of turning classical Hamiltonian mechanics into a quantum theory, essentially. If you’re interested, you can read more about Hamiltonian mechanics here.
The Hamiltonian is made of two parts, the first is the kinetic energy term and the second is the potential term.
In many cases, the systems we’re dealing with are time independent and then the Schrödinger equation takes a simpler form:
\left(-\frac{\hbar^2}{2m}\nabla^2+V\left(x\right)\right)\psi\left(x\right)=E\psi\left(x\right)This is an equation defining the energy of a quantum system, much like in the case of classical mechanics.
Now, why is this relevant to our question? Well, it is precisely because an electron is a quantum mechanical object and therefore, it must fit within this framework of quantum mechanics!
In particular, we can describe everything about the orbits of an electron (which are technically orbitals) around the nucleus by looking at the possible energy levels of the electron.
It turns out that the energy of an electron in an atom is quantized, meaning that there are only very specific values of energy that the electron can have. This, in turn, will help us understand why the electron does not fall into the nucleus.
To a good approximation, we can model an atom as spherical. The simplest atom is the hydrogen atom with one proton and one electron, which will be enough for us – the potential between them is again the Coulomb potential from earlier:
V\left(r\right)=-\frac{e^2}{4\pi\varepsilon_0r}Now, we’re not going to go through solving the Schrödinger equation for the hydrogen atom here since it’s incredibly complicated, all we need are the key results from it.
When solving the full equation, the wave function separates into an angular part and a radial part when using spherical coordinates (r,θ,φ) – these are essentially two angles and a radial distance we use to describe the position of the electron around the nucleus.
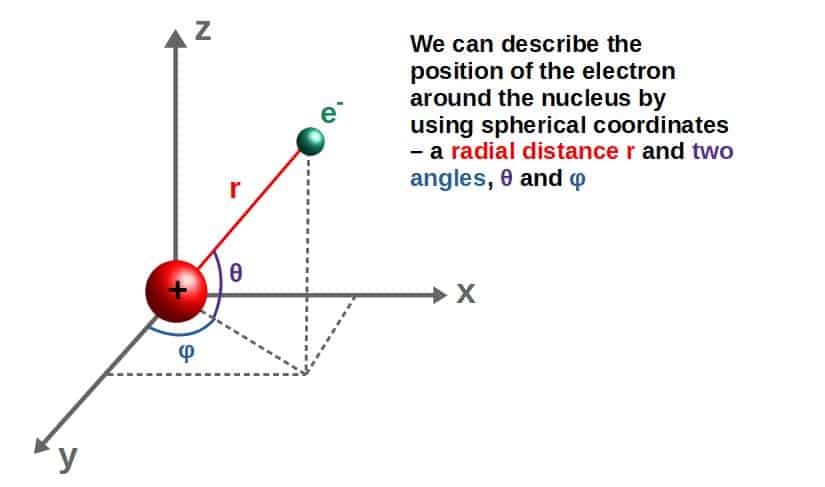
In this case, the wave function, related to the probability of finding the electron at some point (r,θ,φ), takes the following form:

It makes sense to split the wave function like this since the potential is defined purely by radial distance.
Both the radial and the angular part of the wave function can be solved for from the Schrödinger equation, but these generally have quite a complicated form.
However, an interesting feature of these solutions is that they contain something called quantum numbers, which will be important for us.
Now, if we consider the angular part of the wave function, the solution to these are something called spherical harmonics, denoted as Yℓm(θ, φ).
These numbers m and ℓ come up naturally when solving the Schrödinger equation. They’re not just any numbers, they’re both integers with ℓ ≥ 0 and −ℓ ≤ m ≤ ℓ.
This may seem like an insignificant feature but what we have just introduced are two quantum numbers – specifically, m is called the magnetic quantum number and ℓ is the azimuthal quantum number.
Quantum numbers help us to completely describe an atom (but there are more than two!).
We should now retrace our steps and consider the complement to the angular part of the solution, the radial part of the wave function!
The radial part Rℓn(r) cannot be written quite as nicely as the spherical harmonics, however, just like m and ℓ were introduced, we find a third quantum number from the radial solution. This is the principal quantum number n.
Now, how does all of this relate to the question at hand? Well, if we recall the Schrödinger equation from before, there was an energy term on the right-hand side.
In fact, this positive integer n, the principal quantum number, describes the energy levels the electron can have around the nucleus. These energy levels are given by:
E_n=-\frac{m_ee^4}{8h^2\varepsilon_0^2}\frac{1}{n^2}Here, me is the mass of the electron, h is Planck’s constant, n > 0 is the principal quantum number, and as before, e
and ε0 are the charge of the electron and the vacuum permittivity constant.
It is due to these energy levels that electrons do not fall into the nucleus.
Why? Well, quantum mechanics says that the electron can only have energy levels defined by these quantum numbers. The lowest energy that an electron could sit at would be E1, the case with n = 1.
This in fact has a special name, the Rydberg or ground state energy and it has a value of around 13.6 eV (eV are electron volts, a convenient unit of energy).
Now, while these energy levels do not specifically tell us where in the atom the electron can be located at (remember, in quantum mechanics, we can only predict the probability of finding something somewhere), they do indeed tell us that the electron cannot just fall into the nucleus like a classical electron would.
The key to understanding this is that in classical mechanics, ALL electrons would eventually end up falling into the nucleus due to losing energy over time through radiation.
In quantum mechanics, however, bound electrons in an atom have fixed energy levels and they don’t lose energy from radiation – thus, they do not just end up falling into the nucleus after some time.
Now, the very interesting thing is that while an electron doesn’t fall into the nucleus like it classically would, this does not mean that we cannot ever “find” an electron inside the nucleus.
Can An Electron Be Found Inside The Nucleus?
Despite what we have written until now, this does not mean that an electron can never interact with the nucleus. It indeed can!
However, not for the same reason as the classical electron (energy losses resulting in the electron spiraling into the nucleus).
The electron still doesn’t “fall” into the nucleus – instead, it turns out that there is a small, but non-zero probability of finding an electron inside the region occupied by the nucleus.
I want to emphasize the key distinction here – classically, ALL electrons would end up falling into the nucleus, while in quantum mechanics, electrons do not fall into the nucleus, but it is still possible to “randomly” find a particular electron located inside the nucleus.
The process we’re going to discuss next is called electron capture. This is when an electron is essentially “captured” by the nucleus, although the word “capturing” might not describe the phenomenon too accurately.
Recall from earlier, we mentioned that the wave function ψℓnm(r,θ,φ) is related to the probability of finding the electron in a specific place.
A natural question to ask ourselves is; is it possible to find the electron inside of the nucleus?
Let’s look at a specific wave function – the ground state wave functions, which has n=1 and ℓ=m=0. In terms of the radial and angular parts, this wave function would be:
\psi_0^{10}\left(r{,}\theta{,}\varphi\right)=R_0^1\left(r\right)Y_0^0\left(\theta{,}\varphi\right)If we were to do all the math to find the expressions for R01(r) and Y00(θ,φ) from the Schrödinger equation, we’d find the wave function only depends on the radial distance r and it would have the following form:
\psi_0^{10}\left(r\right)=\frac{1}{\sqrt{\pi}}a_0^{-\frac{3}{2}}e^{-\frac{r}{a_0}}Here, a0 is a parameter called the Bohr radius and it is defined as:
a_0=\frac{4\pi\varepsilon_0\hbar^2}{m_ee^2}Physically, the Bohr radius represents the most likely distance away from the nucleus for an electron to be found in a hydrogen atom in its ground state!
Now, let’s plug in r = 0 (which would correspond exactly to the center of the nucleus):
\psi_0^{10}\left(0\right)=\frac{1}{\sqrt{\pi}}a_0^{-\frac{3}{2}}\ne0Interestingly, we find that the wave function is not zero at the center of the nucleus. This allows for the possibility of the probability to find an electron there to not be zero either.
However, the wave function is not directly the same as the probability – instead, the squared magnitude of the wave function is.
Let’s assume that the wave function doesn’t change much inside the nucleus – this makes life easier and is a fairly good assumption since over the length scale of the hydrogen atom, it really doesn’t change that much!
We can also think of the nucleus as a spherical “ball”, essentially.
Then, the probability of finding an electron inside the nucleus is just the probability of finding the
electron at the center multiplied by the volume of the (spherical) nucleus! That is:
Here, r0 represents the radius of the hydrogen nucleus comprised of a single proton.
We can see that the probability to find the electron inside the nucleus depends on the ratio between the size of the nucleus and the size of the Bohr radius (the most likely place to find the electron in its ground state).
The actual value for this probability is really really small – small enough that it may as well be zero for all practical purposes. However, it is crucially non-zero and because of this, new and interesting phenomena are allowed!
This is what enables the aforementioned electron capture.
Simply put, electron capture is when an electron finds itself inside the nucleus of an atom which causes an interaction between that electron and a proton within the nucleus.
In nuclear physics, electron capture is described by the following nuclear equation:
_{_{-1}}^{\ 0}e\ +\ _1^1p\ \Rightarrow\ _0^1n\ +\ _0^0\nu_eOn the left, we have an electron plus a proton and on the right we have a neutron and an electron neutrino.
This equation tells us that in electron capture, an electron reacts with a proton found in the nucleus to produce a neutron and an electron neutrino through some nuclear process (which we’ll look at soon).
The top numbers in the above equation are the relative masses of each component and the bottom numbers are their charges.
You’ll notice that the total mass and charge on both sides are the same – they have to be conserved!
Let’s take a bit more of a detailed look at this interaction. It is a nuclear reaction and, more specifically, it is a weak interaction. Weak in this sense means that it is governed by the weak interaction described in electroweak theory.
The length scale of the weak interaction is very small. So small in fact that it can only take place within a nucleus, hence this phenomenon only occurs when an electron is found here!
You may know or have heard that the photon governs electromagnetic interactions and that it is a “force carrier” particle. Well, the weak force has its own force carrier particles too!
These are called the W and Z bosons. There are, in fact, two W bosons, W+ and W– (the plus and minus represent their charge). The only one we need today is the W+ boson.
In quantum field theories, such as the electroweak theory, we often represent interactions by Feynman diagrams to understand what happens.
We can represent the electron capture interaction and the role of this W+ boson pictorially via a Feynman diagram:
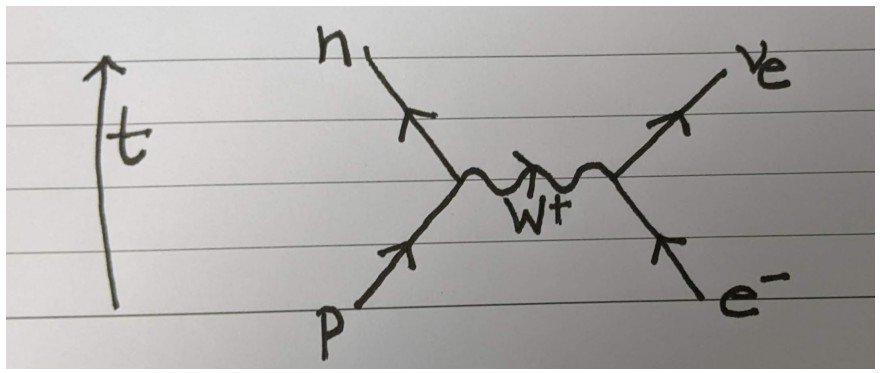
How do we read this? Feynman diagrams are read from the bottom to the top, with time increasing as shown on the left.
The point where arrows meet is called a vertex and represents a quantum interaction. In this case, it is a weak interaction.
A curly line represents a boson (or force carrier particle). The arrows on the straight lines represent the flow of particles, in the sense that an arrow pointing forward in time (i.e. upwards) represent an “ordinary” particle and a backwards arrow represents an antiparticle – though none of these are present here!
Feynman diagrams are an excellent tool for both visualizing quantum interactions but also for doing calculations in quantum field theory!
All in all, this Feynman diagram describes the electron capture phenomenon in the language of quantum field theory.
It says that an electron and a proton can interact by exchange of a W+ boson and this will produce a neutron and an electron neutrino. This is exactly what happens quantum mechanically if an electron somehow finds itself inside the nucleus.
From this, we could also reconstruct the nuclear equation for this interaction that we looked at earlier.
In any case, now we know why electrons cannot just fall into the nucleus in the classical sense, but also that this does not mean that they could not be found there!
Cameron Bunney
I’m a third year PhD student at University of Nottingham, where I also studied my MMath. My main research focus is on curved spacetime QFT and the Unruh effect in analogue gravity systems. I have a soft spot for all kinds of math and physics, from number theory to mathematical biology and everything in between! Aside from research and recreational math, I enjoy playing piano and studying languages.
This article has been co-authored by Cameron Bunney.