Is Lagrangian Mechanics Useful? 9 Key Reasons Why It Absolutely Is
Lagrangian mechanics is a reformulation of classical mechanics that is equivalent to the more commonly used Newton’s laws, but still quite different in many ways.
In this article, I’ll go over the biggest reasons why Lagrangian mechanics is useful and why it’s worth studying.
If you don’t know much about the topic, you may want to read this introductory article on Lagrangian mechanics where I explain what Lagrangian mechanics actually is and what it’s based on.
Lagrangian Mechanics Is Based On An Action Principle
The first really important reason that Lagrangian mechanics so useful is the fact that it is effectively built on one simple (but very profound) idea only; the principle of stationary action.
Essentially, the principle of stationary action states that out of every possible path through space and time, an object will always take the path in which a quantity called action is stationary.
Now, that might sound like a boat load, but to put it simply, this just means that an object will always move in such a way that the action has a stationary value.
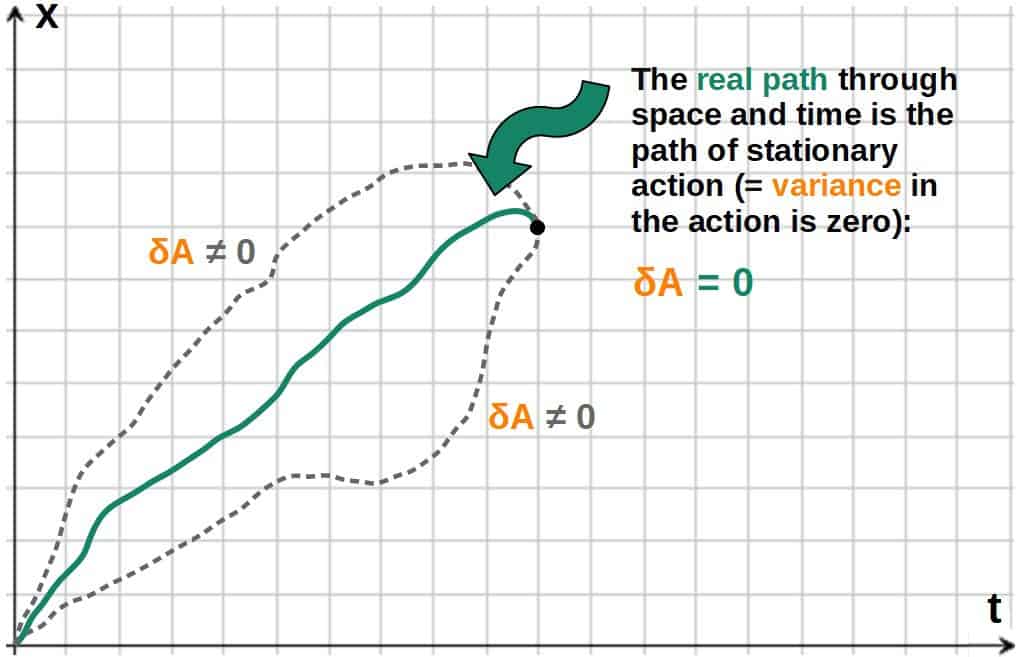
But what even is the action? Essentially, the action is just a quantity assigned with every path that describes that particular path (you could think of it as just a number or a label that each path is defined by).
Now, in Lagrangian mechanics, there is a function called the Lagrangian, which is central to everything. The Lagrangian is simply defined as the difference between kinetic and potential energy:
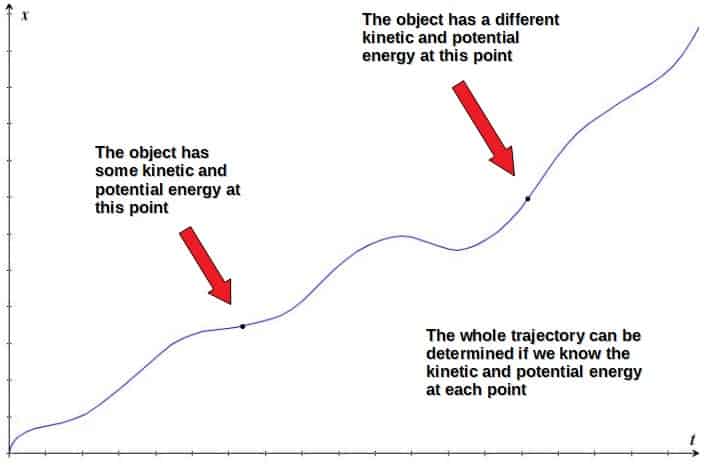
At each point on its path, an object may obviously have a different kinetic and potential energy or in other words, a different value for the Lagrangian.
The kinetic and potential energies are indeed enough to describe the whole trajectory, since by knowing them at every point, we can completely determine how the trajectory would look like.
Now, the action is defined by summing up the values of the Lagrangian at each and every point (i.e. integrated over time since energy is a continuous variable in classical mechanics):
The principle of stationary action can then be mathematically expressed as the variance in the action being zero (it’s really just another way to state that the action is stationary).
The principle of stationary action
There is actually another way of stating this mathematically, which comes from a field of study called calculus of variations; in order for the action to be stationary, the Lagrangian has to satisfy the Euler-Lagrange equations.
The Euler-Lagrange equation
The q’s in the equation represent what are called generalized coordinates, which I’ll explain later in this article.
The key point here, however, is that the principle of stationary action gives us a useful explanation of why objects take certain kinds of trajectories over others and it also gives us the mathematical tools necessary to describe motion in a straightforward manner.

Lagrangian Mechanics Has A Systematic Problem Solving Method
In terms of practical applications, one of the most useful things about Lagrangian mechanics is that it can be used to solve almost any mechanics problem in a systematic and efficient way, usually with much less work than in Newtonian mechanics.
Now, how do you actually do this? First of all, the central thing here is the Euler-Lagrange equations (yes, there are many of them; one for each coordinate q you have).
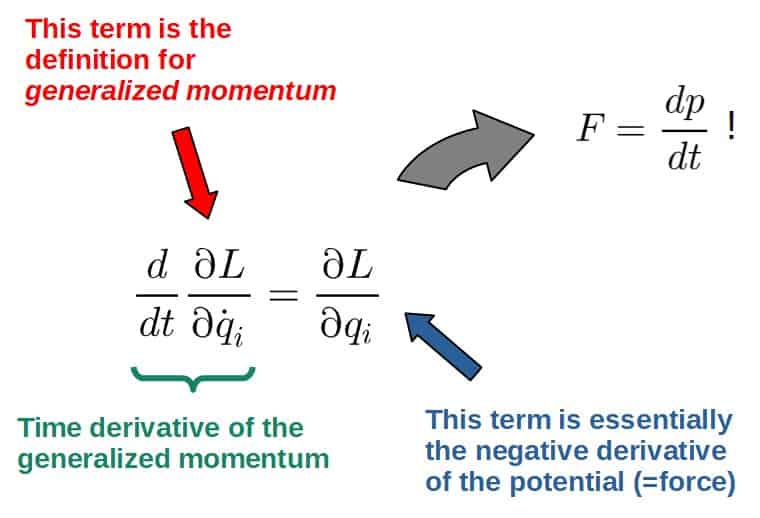
In Lagrangian mechanics, the Euler-Lagrange equation plays the same role as Newton’s second law; it gives you the equations of motion given a specific Lagrangian.
Really the Euler-Lagrange equation is just a reformulation of Newton’s second law. It’s practically F=dp/dt in disguise, just for more general notions of momentum and force:
Now, to get the equations of motion, you just find whatever Lagrangian the system has and then plug it into the Euler-Lagrange equations and it will spit out the full equations of motion.
Essentially, the process for solving almost all problems in Lagrangian mechanics goes more or less like this:
- Find a set of convenient coordinates (= generalized coordinates, expressed by q’s) for the specific problem. These might be the usual Cartesian coordinates (x, y, z), but it is also possible to use coordinate systems such as spherical coordinates (r, θ, φ).
- Define the Lagrangian through the generalized coordinates. The Lagrangian will generally be the sum of the kinetic and potential energies of every object of the system:
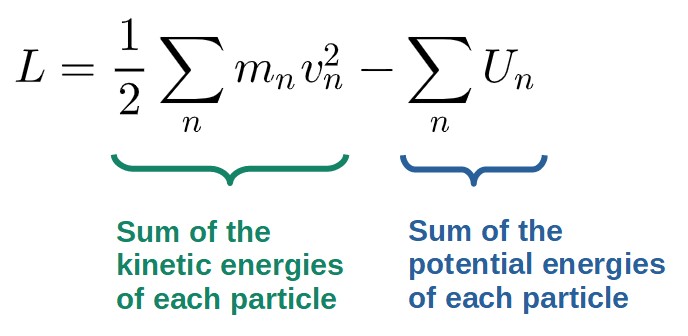
- Plug the Lagrangian into the Euler-Lagrange equations. You’ll have one Euler-Lagrange equation for each generalized coordinate (The q with a dot above means the time derivative of q, i.e. velocity):
- Simplify and solve the differential equations. At this point, you should have one second order differential equation for each generalized coordinate you have.
This is exactly one of the reasons why Lagrangian mechanics is so powerful; there is an extremely general, almost mechanistic process for solving problems.
If this process seems a little too abstract, I’d recommend reading this article where I show lots of examples that essentially follow this exact process. You can also check out my favorite Lagrangian mechanics problem, which also demonstrates this process quite well.
Lagrangian Mechanics Only Uses Scalars
You might have noticed by know that in Lagrangian mechanics, motion is completely described by energies (kinetic and potential energy). This has one really useful property; energy is a scalar, not a vector.
You’re most likely familiar with the use of vectors in Newtonian mechanics, where you have to draw all kinds of vector diagrams and specify forces in each spacial direction etc. In Lagrangian mechanics, you don’t have to do any of that.
The Lagrangian is a scalar function since it only involves energies. In other words, it doesn’t have any specific spacial direction.
Since energy is a scalar of course, it doesn’t have any specific direction. Thus, you’ll never have to draw any vectors or write down the equations of motion separately in each direction like you do when using Newton’s laws.
All you do is specify the kinetic and potential energies for each object in your system, construct the Lagrangian and the equations of motion pretty much pop out automatically (by applying the Euler-Lagrange equations).
Constraints Can Be Incorporated Easily
From Newtonian mechanics, you may be familiar with the idea of constraint forces. These are forces that limit the motion of an object in some specific way.
For a much more comprehensive discussion on constraints and how they work in Lagrangian mechanics, you can read this article.
For example, the tension force in a pendulum is a constraint force since it limits the motion of the pendulum to be in a circle (in other words, the distance from the origin remains constant).
Now, the problem with these constraint forces is that they are specific to a problem and there isn’t a systematic or universal method for specifying them.
Luckily, in Lagrangian mechanics, there is and this is done by using something called Lagrangian multipliers. The way these are used is by specifying a constraint function, which constrains the coordinates (and time) of the given problem in some way:
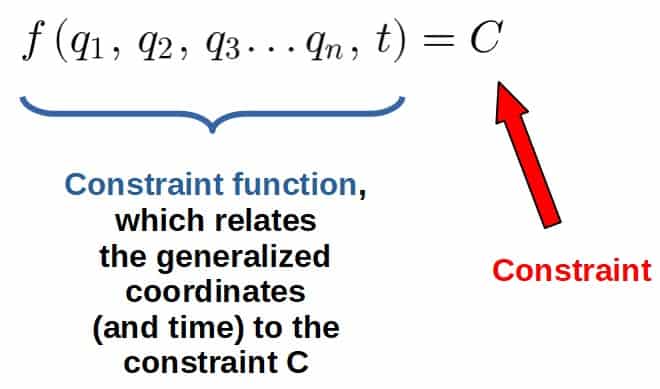
The constraint can then be included in the Lagrangian for the system in the following way:
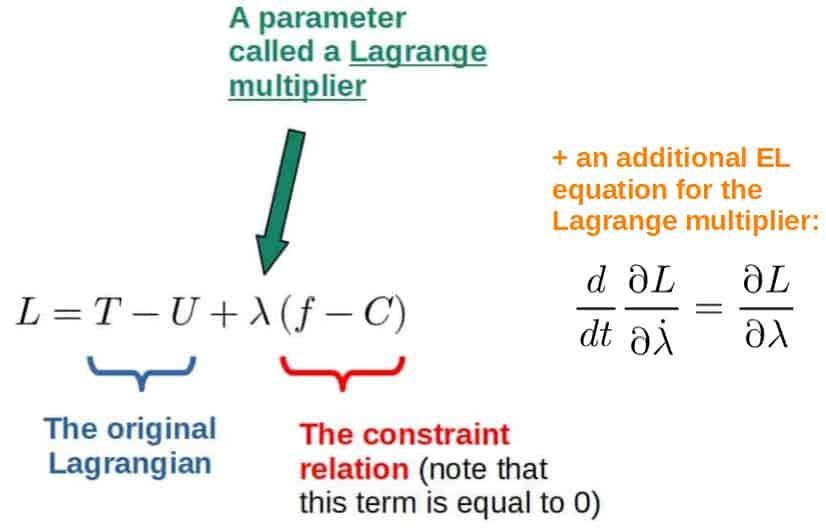
The Lagrange multiplier here is basically what gives us the information about the constraint forces, but in a clever way; all we have to do is specify what the constraint is and add it to the Lagrangian, producing the constrained equations of motion automatically.
Here’s a quick example. For a pendulum (in 2-dimensional Cartesian coordinates), the constraint relation would be the equation of a circle:
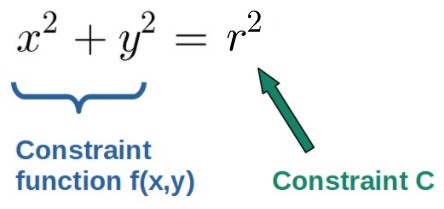
The Lagrangian would then be (with the constraint included):
For the Euler-Lagrange equations, you’d get:
Here, you then have three equations with three unknown variables (x, y, λ), which you can try to solve.
Anyway, this pendulum example demonstrates quite well how the Lagrange multipliers can be used to essentially constrain a system to move in a certain way by using a very simple technique.
Generalized Coordinates Replace Cartesian Coordinates
There is, however, also another way to find equations of motion (constrained or not) that doesn’t require Lagrange multipliers at all, but still gives the same results.
This is by using something called generalized coordinates, which are one of the most important properties of Lagrangian mechanics.
Now, when doing physics problems, we typically use the simple Cartesian coordinate system and this serves the purpose quite well in Newtonian mechanics.
In Lagrangian mechanics, however, we are not limited to any particular coordinate system, but rather, we are free to choose whatever kinds of coordinates we wish.
The beauty of this is that the general rules relating these coordinates are universal, regardless of what coordinates we choose.
Essentially, what this means is that the Euler-Lagrange equations apply in the same way in whatever coordinate system you wish to choose:
These generalized coordinates have a few very useful advantages to the regular Cartesian coordinates:
- Generalized coordinates allow us to implicitly contain ALL information about the constraints (for example, choosing polar coordinates r and θ for a pendulum already includes the fact that the pendulum moves in a circular trajectory).
- The right choice of generalized coordinates can make a calculation extremely simple.
- Generalized coordinates can reduce the number of variables needed in a specific problem.
In case you’re interested to learn more about all of this, I recommend reading my complete guide on generalized coordinates. It will teach you everything you need to know (and much more)!
As an example, instead of the Cartesian coordinate system, you could choose a polar coordinate system, where the coordinates of every point are specified completely specified by the distance from the origin (r) and the angle from the vertical (θ).
Polar coordinates are particularly useful in describing circular motion. Since the coordinates r and θ are by themselves enough to describe a circle, we can completely eliminate the need for Lagrange multipliers this way.
A pendulum is a great example of this. The relation between the x,y -coordinates and the r,θ -coordinates are as follows:
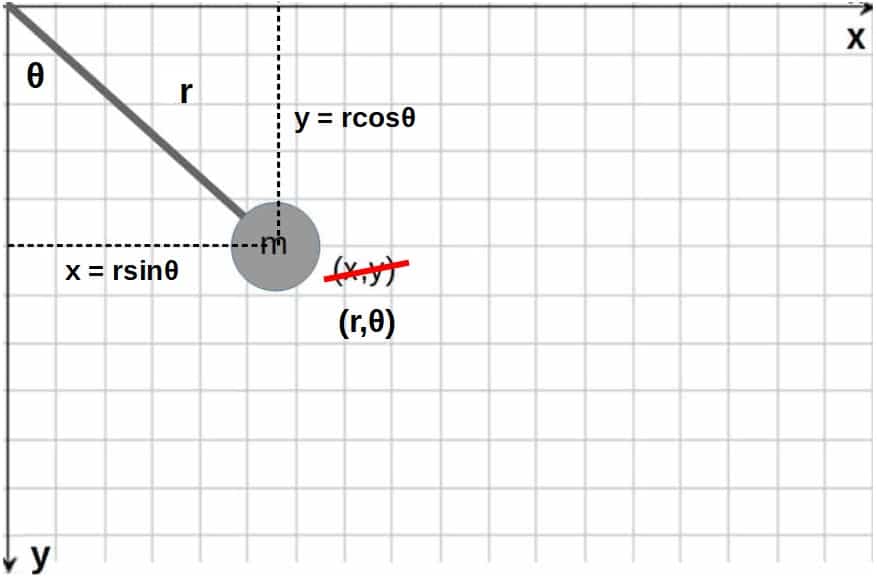
We could insert these into the Lagrangian for a pendulum in the x,y -coordinates and get (note that we don’t have to use the Lagrange multipliers anymore):
Then we simply just write the Euler-Lagrange equations (there is only one of them for θ), from which we get the equation of motion for the pendulum:
Notice a couple useful things with this method of using generalized coordinates:
- We did not have to specify a single constraint; those were already secretly included in our choice of the generalized coordinates.
- Instead of two equations of motion (for both x and y), we have only one (for θ); the angle is the only variable that is changing in polar coordinates.
Conservation Laws Can Be Found Easily (Noether’s Theorem)
In Lagrangian mechanics, there is a simple and straightforward way of analyzing which quantities are conserved in a given system, or in other words, finding conservation laws.
This is done by using something called Noether’s theorem, which can essentially be distilled into one sentence:
For every symmetry in a system, there exists an associated conservation law.
Okay, let’s take a step back. First of all, what does a symmetry even mean? Symmetries in physics and mathematics are a little different than what we usually think they are, but for the context of Lagrangian mechanics, there is a simple definition.
Before I explain that, I’d highly suggest reading this article, which works as a complete guide on Noether’s theorem. It will explain everything you need to know about it in the simplest terms possible. And trust me, Noether’s theorem is definitely a topic you’ll want to learn if you want to go deeper into understanding modern physics.
Now, one way to define a symmetry in physics is the following:
A symmetry in a physical system means that the Lagrangian of that system remains unchanged under a translation of some form (with some caveats to this definition). Associated with this particular transformation (symmetry), there exists a conserved quantity according to Noether’s theorem.
This may seem a little complex, but once you get the hang of it, it really isn’t. There are of course mathematical ways to define Noether’s theorem much more precisely.
If you want a concrete example of this, you can check out the article mentioned above where I show lots and lots of examples of using Noether’s theorem in practice.
Noether’s theorem (in the context of classical mechanics) is extremely useful for three types of conservation laws and their associated translational symmetries:
- Position-translation symmetry (x ⇒ x + Δx) → momentum conservation
- Time-translation symmetry (t ⇒ t + Δt) → energy conservation
- Rotational symmetry (θ ⇒ θ + Δθ) → angular momentum conservation
Anyway, the key point here is that Noether’s theorem gives a simple method for finding conservation laws, which is actually extremely powerful and works for any system you can find a Lagrangian for.
Easily Applied To Other Areas Of Physics
The nice thing about Lagrangian mechanics is that it is highly useful even outside of classical mechanics as well. It’s actually one of the most fundamental ideas that underlie almost all of modern physics.
Well, actually Lagrangians work in a little bit of a different way outside classical mechanics.
What remains the same is the principle of stationary action (which also happens to be the basis for Lagrangian mechanics, but is not at all limited to it).
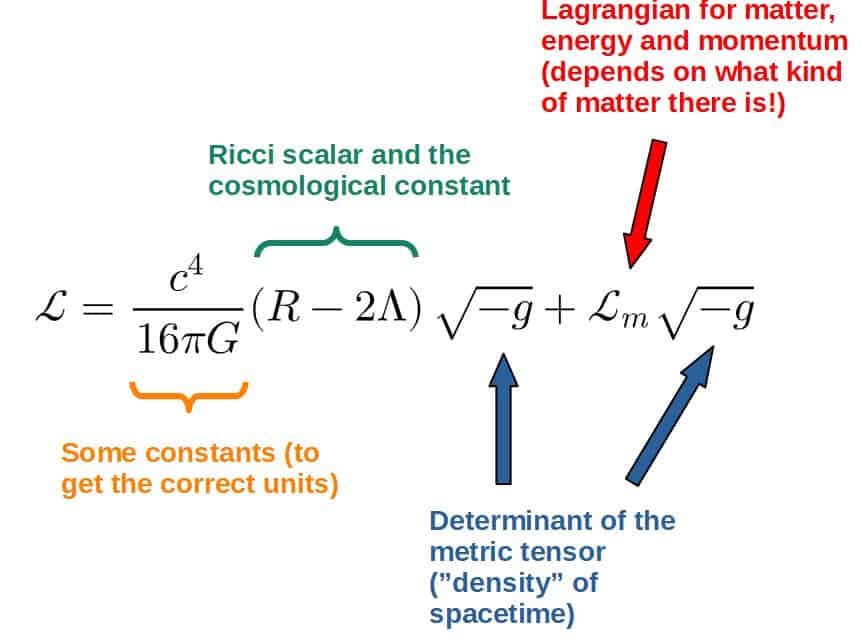
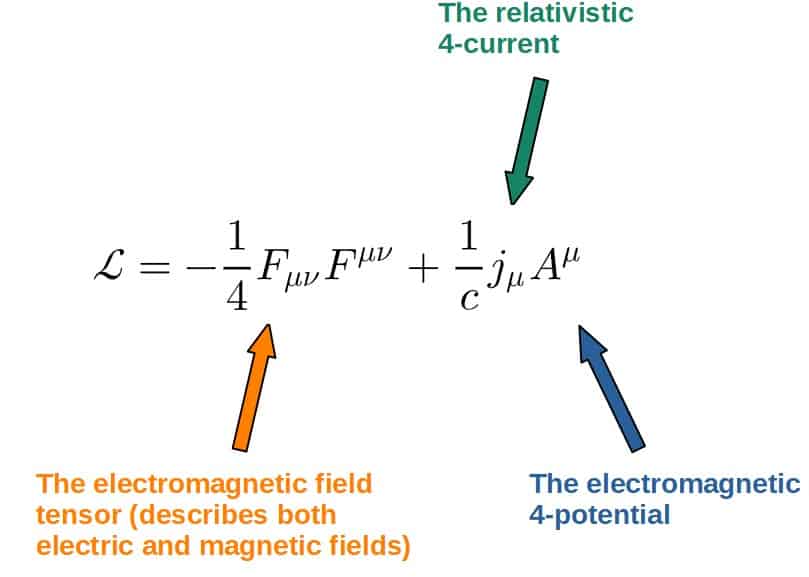
In fact, the reason why it works so well is that the Lagrangian formulation just happens to be a perfect description for fields since fields also obey an action principle.
And it also happens to be that many modern theories of physics are some sort of field theories. General relativity is a field theory, quantum field theory is obviously a field theory, the list goes on.
The main thing to note is that even though fields also obey the principle of stationary action, the Lagrangian will have a different form than just the classical T-U.
Here’s a few Lagrangians, so you can see what I mean (note that these Lagrangians are denoter by a curly L since they are actually Lagrangian densities):
New Laws Of Physics Can Be Found Very Effectively
Now, the action principle being so useful and fundamental in a lot of physics, it is in many cases, the starting point for finding new laws.
In a lot of more modern physics, such quantum field theory and the standard model (which extensively relies on Lagrangians), a useful method to experiment with is constructing a Lagrangian and seeing if something useful would pop out.
Essentially, the process for finding a new law of physics through the action principle would go more or less like this:
- Write down a Lagrangian involving the quantities you’re interested in. In other words, make an educated guess.
- Make sure that the Lagrangian is reasonable. It should have all the necessary properties of good Lagrangians; correct units, Lorentz invariance, gauge invariance etc.
- Apply the principle of stationary action. Write down the corresponding action integral for your Lagrangian and see what happens when it is varied (note that, in many cases, you’ll have to vary the action integral directly since there won’t be a clear notion of the Euler-Lagrange equations).
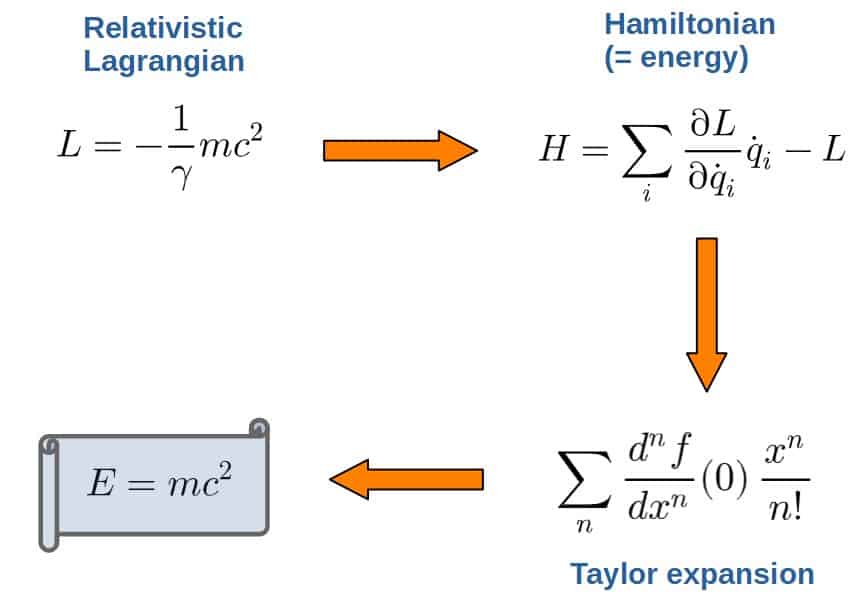
An interesting example of this kind of process can be seen in the derivation of arguably the most famous equation in all of physics, E=mc2.
The process for that would go something like this (if you want to see the whole process, I show it in this article):
Now, it is worth also noting that the method given above isn’t really as much a trial and error -method as it may seem.
There are quite many properties that a useful, potentially valid Lagrangian would have to satisfy and usually these rules narrow the possible choices down to only a few (such as it is with the Lagrangian for general relativity, which I explain briefly in this introduction to general relativity).