Generalized Coordinates: Everything You Need To Know (with examples)

Generalized coordinates are one of the key reasons why other formulations of classical mechanics, such as Lagrangian mechanics, are so useful. However, it’s often not exactly clear what generalized coordinates actually are and why they are so useful.

In classical mechanics, generalized coordinates are a set of parameters that completely specify the configuration of a physical system at each point in time. Generalized coordinates are used to derive the equations of motion for the system, which determine how the coordinates change as functions of time.

In this article, we will be going over the intuition and motivation behind using these generalized coordinates as well as how to actually use them in practice.

The main reason that this article exists is because the topic of generalized coordinates is often skimmed over very briefly in most textbooks and other resources on, for example, Lagrangian mechanics.

However, to me this does not make any sense as generalized coordinates are one of the most important reasons for why the Lagrangian formulation exists in the first place.

Therefore, it is really worth understanding what these generalized coordinates are and why they are useful.

It’s worth noting that generalized coordinates are most commonly used in Lagrangian and Hamiltonian mechanics. If you’re not familiar with these, I recommend reading my introduction to Lagrangian mechanics as well as my introduction to Hamiltonian mechanics (links to both of the articles).

If you really want to go deep into understanding Lagrangian mechanics, you can also check out my full book on the topic – more information can be found here.

What Are Generalized Coordinates, Intuitively?

To put it simply, a set of generalized coordinates is just a set of any parameters that happen to completely describe the configuration of a system.

The “configuration” of a system is just a fancy way of saying the positions in space of each object or part of the system.

We can always place our system into a Cartesian coordinate system, such that the position of each object would described by the x,y,z -coordinates. This would be an example of a set of generalized coordinates.

However, the power of generalized coordinates is that they do not necessarily have to be Cartesian coordinates; generalized coordinates can be pretty much anything that somehow specify the positions of each object in the system.

For example, in problems with rotational symmetries, we’ll often want to choose some angle as our generalized coordinate.

This is perfectly valid in Lagrangian mechanics and in fact, the right choice of generalized coordinates may be the difference between making a problem extremely complicated or making a problem seem almost too easy.

Cartesian Coordinates vs Generalized Coordinates

In classical mechanics, particularly when using Newton’s laws, we’re often used to describing the dynamics of a system in Cartesian coordinates (x,y,z).

However, Cartesian coordinates are not always the best choice for describing a system in the easiest and most effective way possible.

For example, if we have an object in circular motion, the radius from the center must be a constant, so you’d have to account for this fact explicitly when finding the equations of motion for the system in Cartesian coordinates.

Generalized coordinates “fix” exactly this issue. Instead of always using Cartesian coordinates to describe the dynamics of a system, we could use an angle, for example, or any other suitable parameters.

These parameters that completely describe the dynamics of the system are called generalized coordinates.

Essentially, the main difference between Cartesian coordinates and generalized coordinates is that Cartesian coordinates are always the same x, y and z, while generalized coordinates can be any other set of parameters that equivalently specify a point in space.

Now, when using Newton’s laws, it’s often quite difficult to use anything else than Cartesian coordinates, but the Lagrangian formulation makes the use of generalized coordinates extremely easy and effective (I’ll explain this later and also show some examples).

Advantages of Generalized Coordinates: Why Are They Useful?

Before we get to actually finding and using generalized coordinates, it’s worth going over exactly why generalized coordinates are so useful.

Below is a list of the main advantages of generalized coordinates:

• Generalized coordinates allow us to easily describe the dynamics of a system using any parameter.
• Generalized coordinates can often greatly simplify the equations of motion for a system.
• Generalized coordinates can be chosen to implicitly encode all information about the constraints in a system.
• Generalized coordinates often allow us to find conserved quantities in a given system quite easily.

In particular, the third and fourth points here are what really makes the use of generalized coordinates stand out compared to standard Newtonian mechanics.

When using Newton’s laws, whenever we want to constrain a system to behave in a certain way, we have to add in constraint forces that “force” the system to behave in exactly the way we want it to.

For example, when a pendulum is only allowed to swing back and forth with the length of its rod being constant, we have to add in a constraint force that keeps the pendulum at a constant length from the origin; this constraint force is the tension.

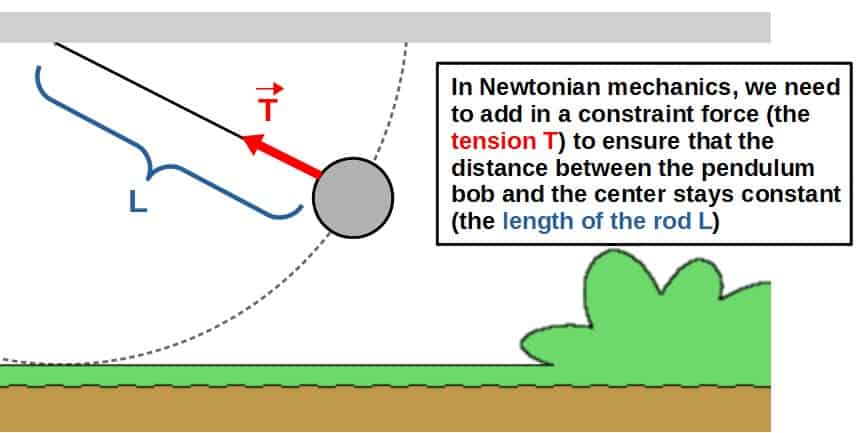
However, when using generalized coordinates, we do not have to add in these constraints by hand; we can, in most cases, choose our generalized coordinates in such a way that they already include the constraints.

If we wanted to, we could add in these constraint forces also in Lagrangian mechanics with the use of Lagrange multipliers, but I want to stress that by using generalized coordinates appropriately, we essentially eliminate the need for any constraint forces.

Also, the other nice thing about generalized coordinates is that they allow us to find conserved quantities much more easily than we would in Newtonian mechanics.

In particular, if we choose some generalized coordinate and the Lagrangian turns out NOT to depend on this particular coordinate, then we immediately know that the corresponding generalized momentum must be conserved.

A more detailed explanation of exactly how the Lagrangian and Newtonian formulations of classical mechanics differ from one another can be found in my article Lagrangian vs Newtonian Mechanics: The Key Differences.

Important Properties of Generalized Coordinates

Before we look at how to find and use generalized coordinates in practice, let’s first discuss some important properties of them.

What are the dimensions of generalized coordinates?

In principle, generalized coordinates can have any dimensions. For example, choosing the radial distance as a generalized coordinate will have dimensions of length, but an angle as a generalized coordinate will be dimensionless.

Do generalized coordinates have to be independent?

Generalized coordinates do not necessarily have to be independent. For example, if certain constraints are included in a system, the generalized coordinates can depend on one another. However, the degrees of freedom in a system always corresponds to the minimum number of independent generalized coordinates.

How To Find Generalized Coordinates

The topic of actually finding suitable generalized coordinates for a given system is a little tricky and that’s simply because there isn’t really a general method to do it.

In other words, finding generalized coordinates for a system is done on a case-by-case basis and it will be different for different problems.

This is largely because generalized coordinates are never unique, meaning that there may be multiple “correct” choices of coordinates for any given problem.

Actually, pretty much any set of coordinates that satisfy the constraints of the problem will be valid choices of generalized coordinates. This is the power of Lagrangian mechanics.

Now, there are still patterns and certain “rules-of-thumb” that you can use when finding generalized coordinates:

1. It’s often worthwhile to look at symmetries in a given problem as this allows you to quickly figure out which generalized coordinates may be suitable.
   • For spherically symmetric problems in 3D, spherical coordinates (radial distance r and two angles, θ and ϕ) are often the best choice, such as in the case of a potential that only depends on the radial distance.
   • Equivalently, for rotational symmetry in 2D, polar coordinates (r and θ) are often suitable.
   • For axisymmetric problems (there is symmetry about one particular axis), cylindrical coordinates will often be the easiest to use.
2. For systems with multiple objects, using relative distances between the objects as generalized coordinates will often work well. An example of this is the two-body problem (explained later).
3. Some helpful questions you may want to think about when choosing generalized coordinates are:
   • Are the coordinates consistent with the specific constraints of the problem? In other words, do the coordinates already include the constraints? If not, use different coordinates or add the constraints in by hand (with Lagrange multipliers).
   • Are the coordinates you’re choosing enough to determine the positions of all objects in the system? You generally need as many generalized coordinates as there are degrees of freedom in the system.

Often, the best place to begin is simply going to be to figure out how many generalized coordinates you’ll need for the given problem in the first place. Luckily, this is quite simple.

The number of degrees of freedom in any given system can be calculated by the formula DN-c, where D is the number of spacial dimensions (1, 2 or 3), N is the number of objects in the system and c is the number of constraints.

The minimum number of independent generalized coordinates you’ll need is then the same as the number of degrees of freedom in the system.

For example, in the case of one object in 2D circular motion, we have D=2, N=1 and c=1 (there is one constraint, which is that the radius of the circle has to be constant), so we would need 2*1-1=1 generalized coordinates (the natural choice in this case would be an angle due to rotational symmetry).

Now, once you have figured out the generalized coordinates you should use, what do you actually do with them in practice?

Perhaps the best tip I could give you here that I do pretty much 100% of the time is write down the Cartesian coordinates (x,y,z) of each object in the system in terms of these generalized coordinates (I’ll show examples of this later).

This is almost always the easiest way to find the Lagrangian, because when you have the x,y,z -coordinates in terms of the generalized coordinates, all you do is take the time derivatives of these and then construct the total kinetic energy (and likewise for the total potential energy) by the formula:

T=\frac{1}{2}\sum_N^{ }m_N\left(\dot x_N^2+\dot y_N^2+\dot z_N^2\right)

This N here denotes the number of objects in the system, so you have to sum over the kinetic energies of all the objects.

This will automatically give you the correct kinetic energy (and potential energy) in terms of your generalized coordinates. The rest is then just constructing the Lagrangian and applying the Euler-Lagrange equations.

Examples of Generalized Coordinates

So far, we’ve only discussed the use of generalized coordinates somewhat abstractly. Therefore, it’s now time to look at some examples to illustrate how exactly generalized coordinates work in practice.

For all of these example, you should keep in mind all of the tips and help questions given earlier, such as “are these coordinates consistent with the constraints?” and “what symmetries does the system have?”.

The Simple Pendulum

The simple pendulum essentially consists of a mass at the end of a rigid rod that swings in a plane under the influence of gravity. The length of the rod is L, the mass of the “pendulum bob” is m and the gravitational acceleration downwards is g (a constant).

We can place the pendulum in an x,y -coordinate system such that the rod is attached to the origin. I’ll also denote the angle relative to the vertical (y-axis) as θ.

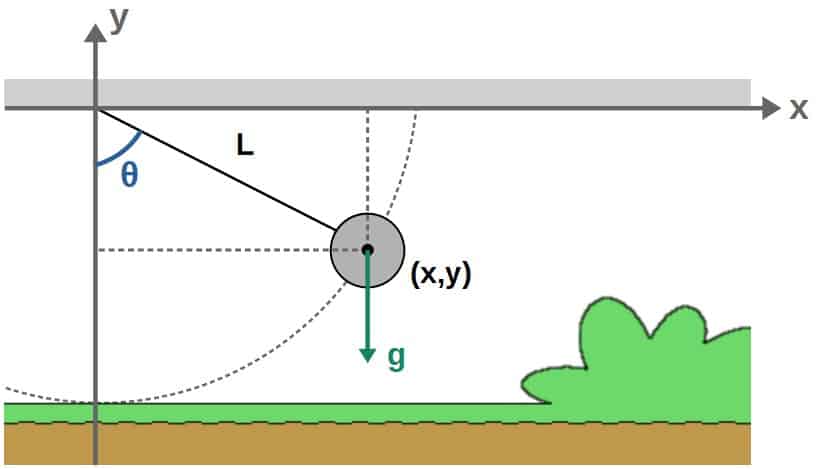
What we want to do is to find the pendulum bob’s position at each point in time and then construct the Lagrangian. To do this, we could use the x,y -coordinates here, but these may not be the best choice.

Let me explain why. First of all, we have once constraint, which is that the length of the rod or the distance from the origin has to be a constant L.

Therefore, we only have 2*1-1=1 (we’re in two dimensions with one object and one constraint) degrees of freedom here and thus, we only need one generalized coordinate.

The natural choice due to rotational symmetry here is going to be the angle θ (which changes with time as the pendulum swings back and forth).

This is indeed a valid choice of a generalized coordinates as it is consistent with our constraint; this θ-coordinate can only change perpendicularly to our constraint (distance from the origin), so it cannot violate this constraint.

So, we will take the angle θ as the generalized coordinate of this pendulum. Now, the easiest way to continue here is to write down the x,y -coordinates in terms of θ. We can get these by some simple trigonometry:

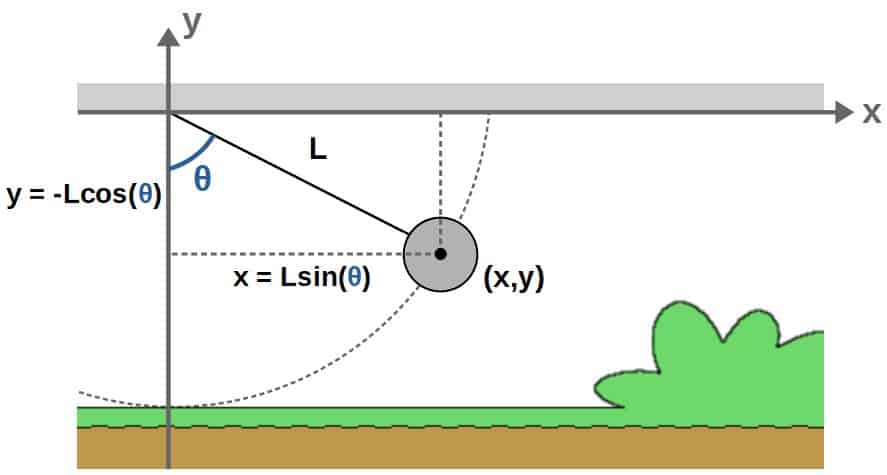
The next step is to construct the kinetic energy. For this, we need the velocities and again, the easiest way to get these is just by differentiating the x,y -coordinates (using the chain rule since θ here is a function of time):

\dot{x}=L\dot{\theta}\cos\theta \dot{y}=L\dot{\theta}\sin\theta

The kinetic energy is then simply:

T=\frac{1}{2}m\left(\dot{x}^2+\dot{y}^2\right)=\frac{1}{2}m\left(L^2\dot{\theta}^2\cos^2\theta+L^2\dot{\theta}^2\sin^2\theta\right)=\frac{1}{2}mL^2\dot{\theta}^2

Here I’ve used cos²θ+sin²θ=1.

Notice how simple obtaining the kinetic energy is if you first write down the Cartesian coordinates in terms of your generalized coordinates. All we need after that is to take the time derivatives and them sum the squares of the Cartesian velocities.

The potential energy is simply going to be V=mgh. If we choose the zero-level of the potential at y=0, then the height h is just the y-coordinate:

V=mgh=-mgL\cos\theta

The Lagrangian is then:

L=T-V=\frac{1}{2}mL^2\dot{\theta}^2+mgL\cos\theta

We now have the Lagrangian of this simple pendulum system in terms of the generalized coordinate θ! You could then use this to calculate the equations of motion from the Euler-Lagrange equation and analyze the motion of the pendulum.

In case you’re interested in how to do that and what it results in physically, I have a free PDF that covers a bunch of Lagrangian mechanics examples, including the simple pendulum. You’ll find the document here.

The Spherical Pendulum

Let’s do another example, this time something a bit more complicated; a pendulum in three dimensions that can swing in all directions. This is called the spherical pendulum and it has some quite interesting properties.

We’ll again call the length of the rod L, the mass m and gravity downwards will be a constant g. We can begin by placing the pendulum in a Cartesian x,y,z -coordinate system:

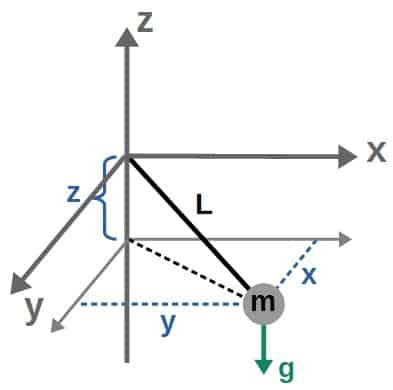
We could use the x,y,z -coordinates of the mass m as our generalized coordinates, but we can again be smarter here; we only need 3*1-1=2 generalized coordinates (we’re in 3 dimensions with one object and one constraint, the distance from the origin has to be a constant L again).

Also, the situation here clearly has some spherical symmetry due to the motion of the pendulum being constrained to a sphere. Therefore, the natural choice of coordinates is going to be two angles, θ and ϕ (these are called spherical coordinates, with the r-coordinate fixed as r=L):

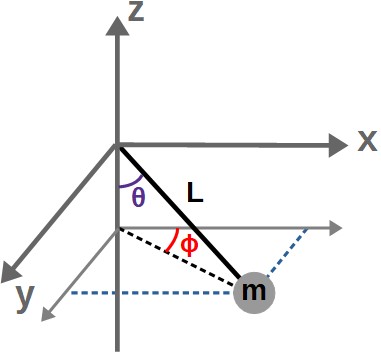
Since we know that at all times, the distance from the origin must be L, we can locate the pendulum bob just by knowing these two angles, θ and ϕ, at any point in time. These will therefore be our generalized coordinates.

It’s again quite simple to figure out the relationship between these generalized coordinates and the Cartesian x,y,z -coordinates. What you’ll end up with are the relations (the derivation of these is also covered in my free Lagrangian mechanics examples PDF):

x=L\sin\theta\cos\phi y=L\sin\theta\sin\phi z=-L\cos\theta

With these relations, constructing the kinetic energy, the potential energy and then the Lagrangian is fairly straightforward. What you’ll end up with is:

L=\frac{1}{2}mL^2\left(\dot{\theta}^2+\dot{\phi}^2\sin^2\theta\right)+mgL\cos\theta

This indeed looks quite similar to the simple pendulum Lagrangian, but the spherical pendulum is a much more interesting system.

For example, there is a certain value of the angle θ where the pendulum will oscillate in a circular motion in the x,y -plane. This, as well as the full derivation of the Lagrangian and the equations of motion for the spherical pendulum are all in my free Lagrangian mechanics PDF found here.

The Two-Body Problem

The two-body problem is one of the most foundational problems in all of classical mechanics as the solutions to it lead to, for example, Kepler’s laws and understanding the elliptical orbits of planets.

Essentially, the two-body problem consists of two objects (masses m₁, m₂) in three dimensions that interact by a potential that depends on the distance between the two bodies (r).

We can begin by describing the positions of both the bodies by some position vectors (i.e. both of the bodies’ x,y,z -coordinates):

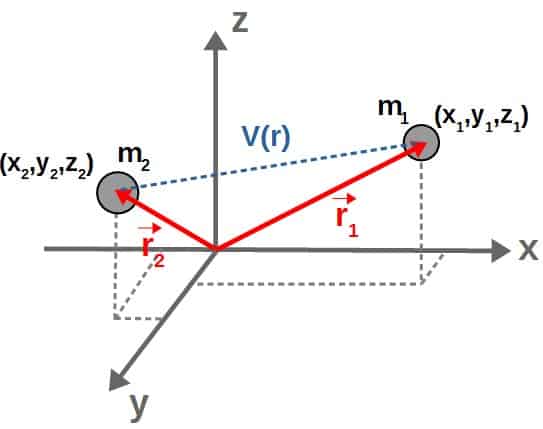
Now, at first it’s not very obvious what constraints we may have here, so it would seem that we need 6 generalized coordinates (3 for both masses) to fully describe this system.

In principle, you could pick the x,y,z -coordinates of both the masses as your generalized coordinates.

However, a better choice is most likely going to be the position of the center of mass of the system as well as the relative distance between the two bodies (since we have a many-body system, a relative distance is going to be a good choice of coordinates most of the time).

These can be described by two vectors, r and R, which both have 3 components (so we still have the necessary 6 degrees of freedom):

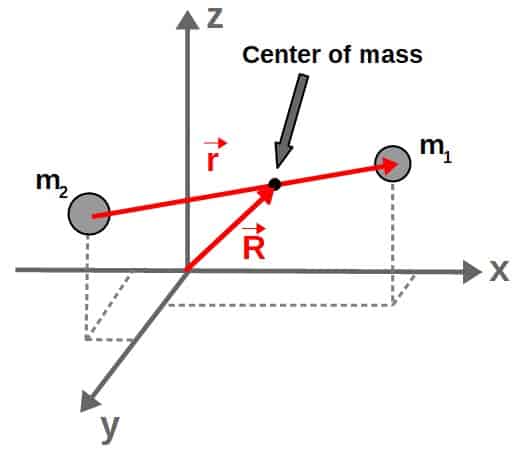
The really nice thing about this choice of coordinates is that since there are no external forces acting on the system, the velocity of the center of mass must be constant.

From this fact, we get three constraints (each of the component of the center of mass -“velocity” vector must be constant). This indeed reduces the degrees of freedom and thus, the required generalized coordinates down to only 3; the 3 components of the relative position vector between the bodies.

Also, since this problem has spherical symmetry, a good choice of generalized coordinates is going to be spherical coordinates.

We can use these if we, for example, choose our coordinates such that one of the masses sits at the origin. The other mass can then be located by a radius r and two angles, θ and ϕ:

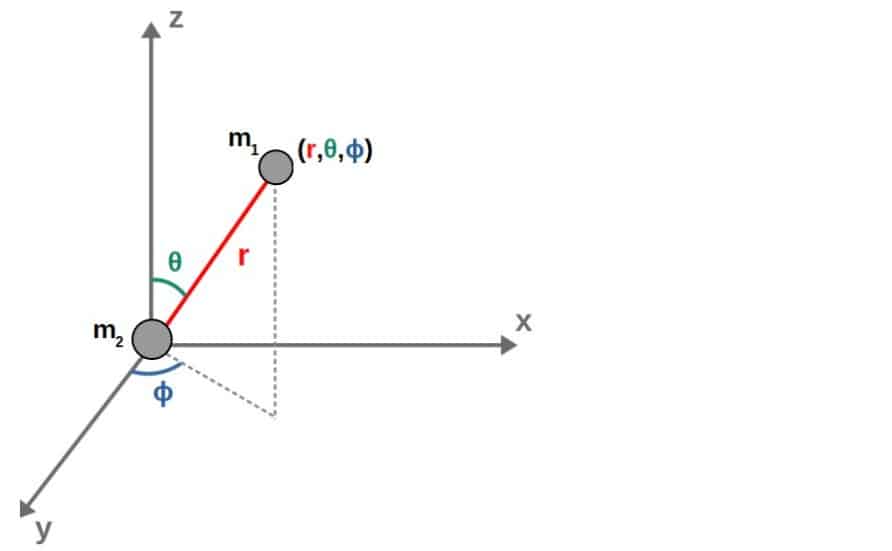
Here we always know that the other mass is located at the origin, so if we know the distance and the two angles (r,θ,ϕ) relative to the mass at the origin, we then know the position of the other mass as well.

Therefore, these 3 coordinates are enough to specify the system and thus, we’ll choose these as our generalized coordinates. The relations between the x,y,z -coordinates of the mass m₁ and these spherical coordinates are:

x=r\sin\theta\cos\phi y=r\sin\theta\sin\phi z=r\cos\theta

These can, once again, be used to construct the Lagrangian by taking time derivatives and so on. The point here isn’t to exactly solve this problem, but to rather show how these generalized coordinates can be chosen.

However, if you’re interested in the solution of the two-body problem, I cover that in the free Lagrangian mechanics example PDF as well (for the case where the potential has the form V(r)∼1/r, which is the gravitational potential; this leads to various cool results such as elliptical orbits).