Lagrangian Mechanics With Friction: A Step-By-Step Guide With Examples
You may have heard that Lagrangian mechanics can only deal with conservative systems, i.e. systems where no energy is “lost”. Does this mean that there is no way to include things like friction and non-conservative forces?
Generally, there are two ways to include friction and non-conservative forces in Lagrangian mechanics: one is by using a modified time-dependent Lagrangian and the other is by using a dissipation function that essentially accounts for the energy lost from friction or a non-conservative force.
I’ll explain these two ways in detail in this article deal and also show some examples later of dealing with different types of friction in Lagrangian mechanics.
Quick tip: To learn more about advanced topics like friction in Lagrangian mechanics (and many more), I’d highly recommend checking out my book Lagrangian Mechanics For The Non-Physicist (link to the book page). This book will teach you everything you need to know about Lagrangian mechanics and its applications as well as all kinds of advanced topics like the one discussed in this article.
How Can Friction and Non-Conservative Forces Be Included In Lagrangian Mechanics?
Generally, there are two methods to include friction in Lagrangian mechanics (the second one being the more general, while the first one works only in special cases):
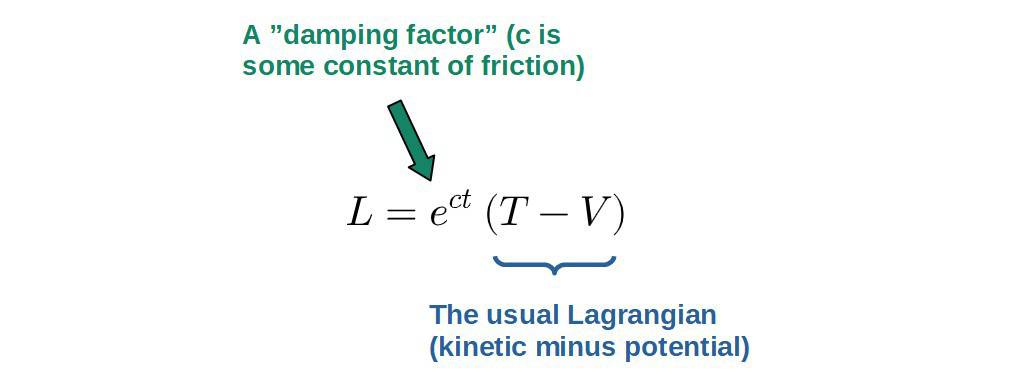
- A modified Lagrangian (with an exponential time-dependent “damping term” that essentially takes into account changes in the Lagrangian due to energy being lost from friction):
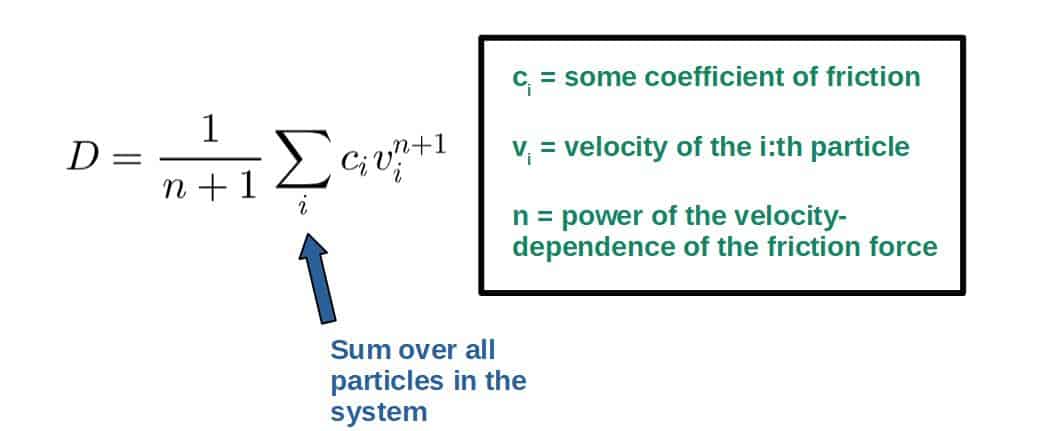
- The general dissipation function (the special case of this where n=1 is known as Rayleigh’s dissipation function):
Now, this article is obviously going to include a lot about Lagrangian mechanics so if you’re not very familiar with the formulation yet, I’d recommend reading my introduction to Lagrangian mechanics.
Anyway, let’s get started!
The Modified Lagrangian
The first way friction can be incorporated into Lagrangian mechanics is by using a modified time-dependent Lagrangian.
No, this method is not necessarily the best and later I’ll show a better and more general way, but a modified Lagrangian does work well for one case; linear velocity-dependent friction. What does that mean, though?
Essentially, linear velocity-dependent friction means a friction force that is directly proportional to the velocity v and not some other power of velocity, such as v2. In other words, the friction increases linearly with the velocity.
Mathematically, these kinds of linear friction forces are expressed as:
F=-cvThe c here is some proportionality constant; it is usually some kind of coefficient of friction that will depend on the specific substance an object is moving in etc.
By using the little modification exponential term to the Lagrangian, it is possible to obtain the correct equations of motion that also include friction (down below I’ve included an example of this).
The modified Lagrangian for linear friction:
L=e^{ct}\left(T-V\right)
For this example, let’s assume that an object is moving in the x-direction under no potential energy. In this case, its velocity is dx/dt (which we’ll here denote as \dot{x}) and its kinetic energy is:
T=\frac{1}{2}m\dot x^2The modified Lagrangian is then (we’ll leave the constant as just the unspecified c for now, but you could define it in some other way if you wanted to):
L=e^{ct}\left(\frac{1}{2}m\dot{x}^2\right)=\frac{1}{2}e^{ct}m\dot x^2The coordinate we’re interested in is, of course, x. The Euler-Lagrange equations will then be:
\frac{d}{dt}\frac{\partial L}{\partial \dot x}=\frac{\partial L}{\partial x}Plugging in the Lagrangian, we get:
\frac{d}{dt}\frac{\partial}{\partial \dot x}\left(\frac{1}{2}e^{ct}m\dot{x}^2\right)=\frac{\partial}{\partial x}\left(\frac{1}{2}e^{ct}m\dot{x}^2\right)The right hand side will be just zero, since the Lagrangian doesn’t contain x by itself. From the left side, we have:
\frac{d}{dt}\left(e^{ct}m\dot{x}\right)=0Here, both the x-dot and the exponential thing depend on time, so we have to use the product rule:
\frac{d}{dt}\left(e^{ct}m\dot{x}\right)=m\dot{x}\frac{d}{dt}e^{ct}+e^{ct}\frac{d}{dt}m\dot{x}=0Taking these derivatives, we get (in the second term, we just add another time derivative to get \ddot{x}):
m\dot{x} ce^{ct}+e^{ct}m\ddot{x}=0Here, we can divide out the ect -term and move some things around:
m\ddot{x}=-cm\dot{x}This thing on the right is, of course, is just the friction force in the form F=-cv. The term on the right is simply mass times acceleration, ma.
Now, this constant c doesn’t really matter too much, but you could specify it as something. For example, if you define the constant as the following, you’ll recover Stokes’ law:
c=\frac{6\pi\mu R}{m}Now, this modified Lagrangian only works for linear drag, so you can’t include things like quadratic drag or friction due to normal force. If you wish to include these, you’ll have to use a dissipation function.

The General Dissipation Function
The general dissipation function is, in my opinion, one of the most interesting extensions to the Lagrangian formulation.
Typically, most people only know about something called Rayleigh’s dissipation function and simply assume that things like friction due to a normal force can’t be included. This is simply not true.
Rayleigh’s dissipation function is only a special case of a more general formula (in particular, the case where n=1, i.e. for linear friction), which I call the general dissipation function.
The general dissipation function:
D=\frac{1}{n+1}\sum_j^{ }c_jv_j^{n+1}
Note that here I’ve changed the summation index to j (which was i earlier), simply to avoid confusion when we add this thing to the Euler-Lagrange equations.
Anyway, the first question you may have is; what does this function have to do with dissipation? Well, the answer is that this function indeed holds information about the energy “lost” from friction.
In fact, the dissipation function describes the rate of change of the work done by the friction force (i.e. power):
D=-\frac{1}{n+1}\frac{dW}{dt}=-\frac{1}{n+1}PThe minus sign comes from the fact that energy is “lost” in frictional processes.
The proof of this is shown down below.
Now, generally, friction forces are always modeled as being proportional to some power of velocity (which might vary depending on the situation):
F=-cv^nLet’s look at the dissipation function again (we can drop the summation indices, since they won’t matter here). Particularly, we can express it as:
D=\frac{1}{n+1}cv^{n+1}=\frac{1}{n+1}cv^n\cdot vNow, cvn is just minus the friction force (see above):
D=\frac{1}{n+1}cv^n\cdot v=\frac{1}{n+1}\left(-F\right)\cdot v=-\frac{1}{n+1}F\cdot vLet’s now look at the definition of power, which is the rate of change of the work done by whatever force is in question (here it is a friction force):
P=\frac{dW}{dt}Now, the work done can be expressed as an integral over a certain path C of the force and the distance moved, dr. The power is then:
W=\int_C^{ }F\cdot dr\ \ \Rightarrow\ \ P=\frac{dW}{dt}=\frac{d}{dt}\int_C^{ }F\cdot drBut, we also know from the definition of velocity:
v=\frac{dr}{dt}\ \ \Rightarrow\ \ dr=vdtInserting this to the integral above, we get:
P=\frac{d}{dt}\int_C^{ }F\cdot dr=\frac{d}{dt}\int_C^{ }F\cdot vdtHere, we have a derivative of an integral (both with respect to time), so the integral and derivative basically “cancel” and we’re left with:
P=\frac{dW}{dt}=F\cdot vThis is, of course, just what we had in the dissipation function:
D=-\frac{1}{n+1}F\cdot v\ \ \ \Rightarrow\ \ \ D=-\frac{1}{n+1}PQuick tip: In my book Lagrangian Mechanics For The Non-Physicist, we discuss the dissipation function formulation MUCH more deeply – more than you’ll find in any currently existing textbook – beginning entirely from first principles. There, we, for example, derive the dissipation function from the concept of so-called generalized forces, and build a relation between the two.
The next question is; what do you actually do with this dissipation function? Essentially, the dissipation function is added to the Euler-Lagrange equations as a generalized force:

Now, what specifically is this generalized force? First of all, we know that conservative forces are defined as negative positional gradients of a potential energy.
Analogous to that, non-conservative forces (i.e. friction) are defined as negative velocity gradients of the dissipation function (I’m denoting the frictional forces specifically by an f-index):
Q_i^f=-\nabla_vDEssentially, the dissipation function can be thought of as some kind of potential for non-conservative forces.
In Lagrangian mechanics, however, we want to express everything in terms of generalized coordinates (q’s), so this would actually be the derivative with respect to the generalized velocity:
Q_i^f=-\frac{\partial D}{\partial \dot q_i}The Euler-Lagrange equations with friction included are then:
\frac{d}{dt}\frac{\partial L}{\partial\dot{q}_i}=\frac{\partial L}{\partial q_i}-\frac{\partial D}{\partial\dot{q}_i}\ {,}\ \ D=\frac{1}{n+1}\sum_j^{ }c_jv_j^{n+1}
Down below I’ve included a bunch of examples of how to actually use this as well as a general step-by-step process of how to calculate stuff in Lagrangian mechanics with friction included.
How To Include Friction in Lagrangian Mechanics (Step-By-Step Examples)
Generally, the process for using the dissipation function in Lagrangian mechanics goes more or less like this:
- Specify the total velocity of each object in the system using whatever coordinates you wish. These could be the regular Cartesian coordinates (x,y,z) of whatever other generalized coordinates, such as an angle θ in rotational motion.
- Specify the coefficients of friction for each object in the system. This step can also be done later, since the coefficients won’t affect the calculations even if left unspecified. Also note that the coefficients may sometimes time-dependent; cj = cj(t).
- Write down the dissipation function for the given system. If the system has multiple object, the dissipation function will have a sum over the velocities and friction coefficients of each object.
- Calculate the Euler-Lagrange equations with the dissipation function included. Note that you will have one equation for each generalized coordinate.
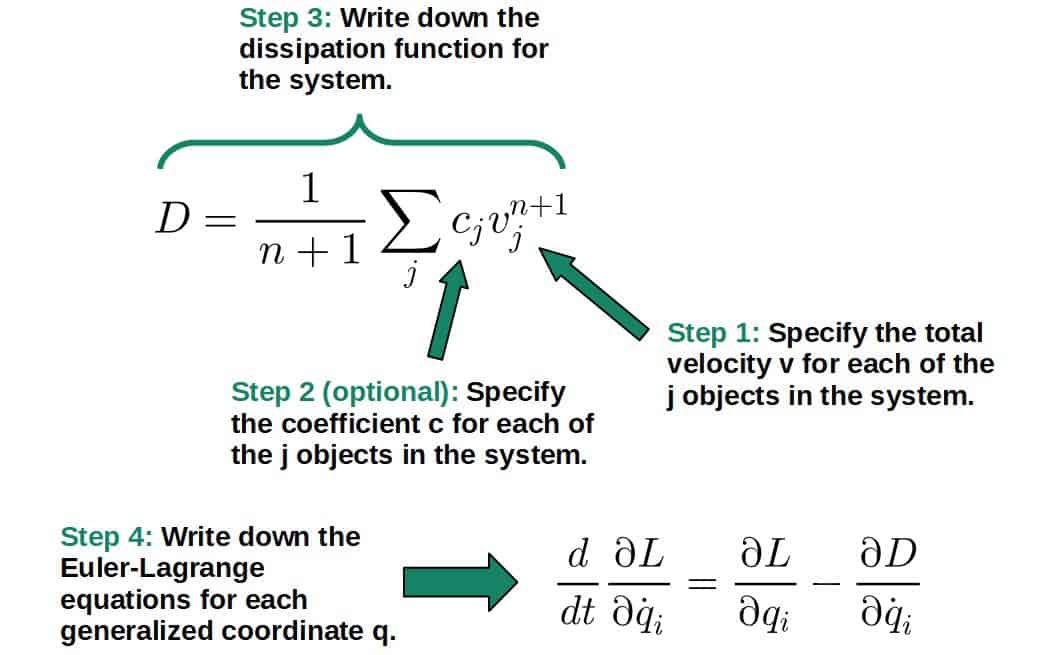
Down below I have a step-by-step example of pretty much all the cases you might want to use this method for.
Friction Due To Normal Force
In Newtonian mechanics, we know that if an object is moving along a surface, there will be a frictional force (this is called kinetic friction) asserted by the particular surface in question.
This force will only be opposite to the direction of motion (as is the case for all friction forces).
The kinetic friction force is given by the formula (the object has to be at rest vertically in order to stay in contact with the surface, i.e. the normal force has to equal the gravitational force):
F=\mu N=\mu mgNow, this force is not proportional to velocity at all, so how do we use the dissipation function for this kind of friction? The answer is actually very simple; the friction due to normal force is proportional to the 0th power of velocity (i.e. just one, since v0=1).
Recall the dissipation function again:
D=\frac{1}{n+1}\sum_j^{ }c_jv_j^{n+1}For this example, we will take an object moving along a horizontal surface in the x-direction. This means that we can drop the summation since we only have one object. The velocity will then be in the x-direction (i.e. time derivative of x, which we’ll denote again as \dot{x}):
v=\frac{dx}{dt}=\dot xSince the friction due to normal force can be thought of as being proportional to the 0th power of velocity (which means setting n=0), the dissipation function becomes:
D=\frac{1}{0+1}c\dot{x}^{0+1}=c\dot xNow, what do we want this constant c to be? Well, think about the friction force again; F=µmg. These are all constants, so we can define c as c=µmg. We then have the finished dissipation function.
Dissipation function for friction due to normal force:
D=\mu mg\dot{x}
Now it’s only a matter of finding the Lagrangian and obtaining the equations of motion from the Euler-Lagrange equations. This can be seen down below.
We already have the specific dissipation function for this system, but we also need the Lagrangian to get the equations of motion.
The Lagrangian is particularly simple for this case. Since the object is moving along the horizontal (x-direction), the potential energy won’t play any role here. Thus, the Lagrangian is only the kinetic energy (T=1/2mv2):
L=T=\frac{1}{2}m\dot{x}^2Here, we can then plug the Lagrangian as well as the dissipation function into the Euler-Lagrange equations:
\frac{d}{dt}\frac{\partial L}{\partial\dot{x}}=\frac{\partial L}{\partial x}-\frac{\partial D}{\partial \dot x} \frac{d}{dt}\frac{\partial}{\partial\dot{x}}\left(\frac{1}{2}m\dot{x}^2\right)=\frac{\partial}{\partial x}\left(\frac{1}{2}m\dot{x}^2\right)-\frac{\partial}{\partial\dot{x}}\left(\mu mg\dot{x}\right) \frac{d}{dt}\left(m\dot{x}\right)=0-\mu mg\ \ \ \Rightarrow\ \ \ \ddot{x}=-\mu gThis is, of course, what we would expect to get. The acceleration in the x-direction is the acceleration from friction that opposes the direction of motion (which can be seen form the minus sign).
Linear Velocity-Dependent Friction
This example will include a friction force that is proportional to the first power of velocity, i.e. linear friction. Now, we already did this earlier with the modified Lagrangian, but it’s worth showing that it works here also.
What we specifically want to do is derive Stokes’s law for an object moving again in the x-direction. Stokes’ law in Newtonian mechanics (i.e. using forces) is:
F=6\pi\mu RvNow, since the force is linear in the velocity, this means that the n in our dissipation function is going to be n=1. Also, the velocity is purely in the x-direction, so the dissipation function is (we’ve also dropped the summation, since there is only one object):
D=\frac{1}{1+1}c\dot{x}^{1+1}=\frac{1}{2}c\dot{x}^2If you’ve seen Lagrangian mechanics with friction before, you may notice that this is actually the commonly used Rayleigh’s dissipation function.
All we need anymore is the constant c. We know that the force should be F=6\pi\mu Rv, so therefore the coefficient c should be c=6\pi\mu R. The dissipation function is then:
Dissipation function for Stokes’ law (linear friction):
D=3\pi\mu R\dot{x}^2
From this, we can easily obtain the equations of motion and derive Stokes’ law for this particular system.
We know that the Lagrangian for this particular system (object moving only in the x-direction; i.e. no potential energy term) should be simply the kinetic energy:
L=\frac{1}{2}m\dot{x}^2Now we simply plug this and the dissipation function into the Euler-Lagrange equations:
\frac{d}{dt}\frac{\partial L}{\partial\dot{x}}=\frac{\partial L}{\partial x}-\frac{\partial D}{\partial \dot x} \frac{d}{dt}\frac{\partial}{\partial\dot{x}}\left(\frac{1}{2}m\dot{x}^2\right)=\frac{\partial}{\partial x}\left(\frac{1}{2}m\dot{x}^2\right)-\frac{\partial}{\partial\dot{x}}\left(3\pi\mu R\dot{x}^2\right) \frac{d}{dt}\left(m\dot{x}\right)=0-2\cdot3\pi\mu R\dot{x}\ \ \ \Rightarrow\ \ \ m\ddot{x}=-6\pi\mu R\dot{x}Quadratic Velocity-Dependent Friction
Typically, people think that quadratic friction can’t be included in Lagrangian mechanics.
This is true if you’re just using the more commonly known Rayleigh’s dissipation function, however, with the general dissipation function, we can indeed include quadratic friction as well (or any other power of velocity-dependence).
Now, quadratic friction means a friction force that is proportional to the square of the velocity, v2.
Typically, this shows up in the drag equation (for example, when describing air resistance up to a certain extent; you can read more about it on NASA’s webpage):
F=\frac{1}{2}\rho C_DAv^2We will again take a single object moving in the x-direction. The velocity-dependence should, in this case, be quadratic, so we’ll define n=2. The dissipation function then becomes:
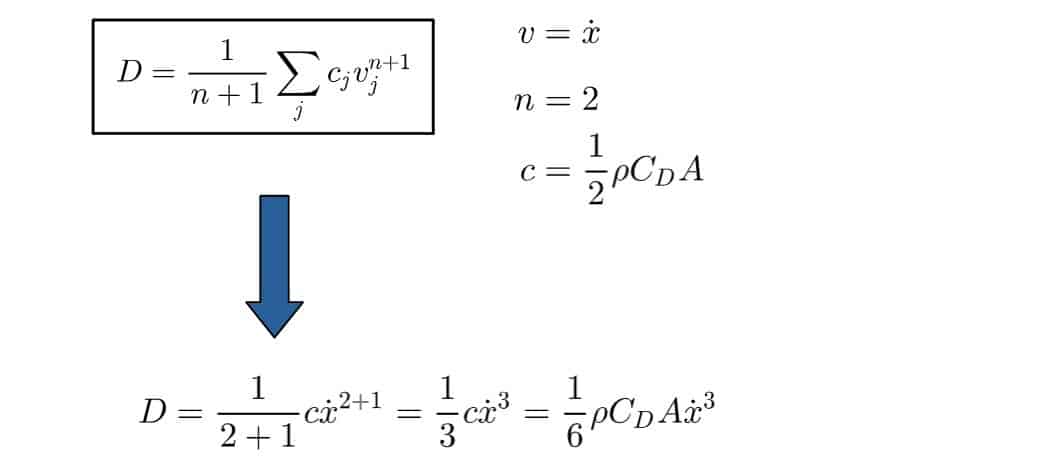
Dissipation function for the drag equation (quadratic friction):
D=\frac{1}{6}\rho C_DA\dot{x}^3
The equations of motion (i.e. the drag equation in the x-direction) is then easily obtained from using the Euler-Lagrange equations. This is shown down below.
The Lagrangian for this system will be just the kinetic energy (since the object is only moving in the horizontal direction; the potential energy doesn’t play any role) as seen in the earlier examples too:
L=\frac{1}{2}m\dot{x}^2Plugging this Lagrangian and the dissipation function into the Euler-Lagrange equations, we obtain:
\frac{d}{dt}\frac{\partial L}{\partial\dot{x}}=\frac{\partial L}{\partial x}-\frac{\partial D}{\partial \dot x} \frac{d}{dt}\frac{\partial}{\partial\dot{x}}\left(\frac{1}{2}m\dot{x}^2\right)=\frac{\partial}{\partial x}\left(\frac{1}{2}m\dot{x}^2\right)-\frac{\partial}{\partial\dot{x}}\left(\frac{1}{6}\rho C_DA\dot{x}^3\right) \frac{d}{dt}\left(m\dot{x}\right)=0-3\cdot\frac{1}{6}\rho C_DA\dot{x}^2\ \ \ \Rightarrow\ \ \ m\ddot{x}=-\frac{1}{2}\rho C_DA\dot{x}^2This is, of course, just the drag equation (in the x-direction) that we were expecting to get.

Pendulum With Friction (Using Generalized Coordinates)
This next example is going to be quite interesting and a little different than the above ones. In this one, we will use one of the key advantages of Lagrangian mechanics; generalized coordinates.
If you don’t know what generalized coordinates are or what they’re used for, I’d recommend reading about them in this article. I also show an example comparing the usefulness of them to the Newtonian mechanics approach in this article.
Essentially, what we’re going to do is find the equations of motion for a pendulum with friction (air resistance).
The way we’ll do this is by choosing our generalized coordinate to be the angle to the vertical, θ (we only need to know the angle to determine the motion of the pendulum) instead of the typical x and y coordinates. Everything we need can be seen in the picture below.
This is exactly the essence of using generalized coordinates; we can choose to describe the system by whatever coordinates we wish. All we need to do is convert from the x,y -coordinate system to the generalized coordinate system.
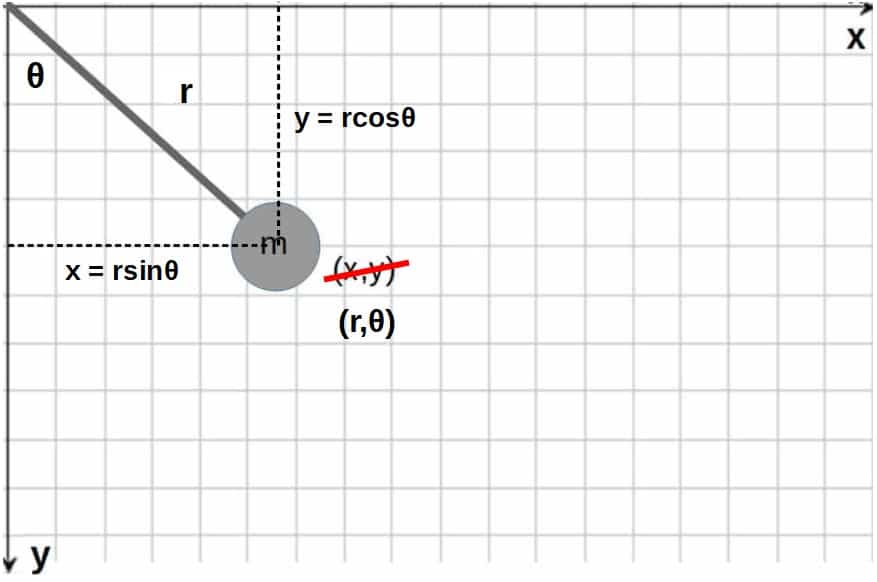
Essentially, the relationship between the x and y -coordinates and the coordinate θ are the following:
x=r\sin\theta\ {,}\ \ y=r\cos\thetaThe velocities in each direction are then simply the time derivatives of these (note that θ here changes with time, so we have to use the chain rule):
\dot{x}=r\dot{\theta}\cos\theta\ {,}\ \ \dot{y}=-r\dot{\theta}\sin\thetaHere, \dot{\theta} is the time derivative of θ.
The total velocity is then simply (by the Pythagorean theorem):
v=\sqrt{\dot{x}^2+\dot{y}^2}=\sqrt{\left(r\dot{\theta}\cos\theta\right)^2+\left(-r\dot{\theta}\sin\theta\right)^2}=\sqrt{r^2\dot{\theta}^2\left(\cos^2\theta+\sin^2\theta\right)}We know that sin2θ + cos2θ = 1, so the velocity is then:
v=\sqrt{r^2\dot{\theta}^2\left(\cos^2\theta+\sin^2\theta\right)}=\sqrt{r^2\dot{\theta}^2}=r\dot \thetaIf we now assume that the pendulum is moving with a reasonably normal velocity, the air resistance will be simply given by the Stokes’ law.
Now, we already derived earlier what the dissipation function for Stokes’ law is (the R here is the radius of the spherical pendulum bob, but that’s not too important; it’s simply some constant):
D=3\pi\mu Rv^2This dissipation function can easily be converted to generalized coordinates (in our case, to be a function of \dot{\theta} instead of \dot{x} or \dot{y}); all we do is insert the total velocity we calculated earlier:
D=3\pi\mu Rv^2\ \ \left(v=r\dot{\theta}\right)\Rightarrow\ \ D=3\pi\mu Rr^2\dot{\theta}^2Dissipation function in terms of a generalized coordinate θ (for linear friction):
D=3\pi\mu Rr^2\dot{\theta}^2
From this, all we have to do is find the Lagrangian and then calculate the equations of motion from an Euler-Lagrange equation for our generalized coordinate θ. This is shown down below.
First of all, the kinetic energy for the pendulum bob will be simply T=1/2mv2. This, we can convert to our generalized coordinates by inserting the velocity we already obtained before:
T=\frac{1}{2}mv^2\ \ \left(v=r\dot{\theta}\right)\Rightarrow\ \ T=\frac{1}{2}mr^2\dot{\theta}^2For the pendulum, we also need its potential energy. If we choose the zero-level of the potential to be at the x-axis, then the potential energy will be simply V=mgy (since the height of the pendulum bob is basically the y-coordinate).
This can be converted to be function of θ by using the relationship between the y-coordinate and θ (see the picture from earlier):
V=mgy\ \ \ \left(y=r\cos\theta\right)\Rightarrow\ \ V=mgr\cos\thetaThe Lagrangian for this pendulum bob will then be:
L=T-V=\frac{1}{2}mr^2\dot{\theta}^2-mgr\cos\thetaNow, plugging this thing and the dissipation function we got earlier into the Euler-Lagrange equations will give us (we now have the Euler-Lagrange equation for the coordinate θ instead of x):
\frac{d}{dt}\frac{\partial L}{\partial\dot{\theta}}=\frac{\partial L}{\partial\theta}-\frac{\partial D}{\partial\dot{\theta}} \frac{d}{dt}\frac{\partial}{\partial\dot{\theta}}\left(\frac{1}{2}mr^2\dot{\theta}^2-mgr\cos\theta\right)=\frac{\partial}{\partial\theta}\left(\frac{1}{2}mr^2\dot{\theta}^2-mgr\cos\theta\right)-\frac{\partial}{\partial\dot{\theta}}\left(3\pi\mu Rr^2\dot{\theta}^2\right) \frac{d}{dt}\left(mr^2\dot{\theta}\right)=mgr\sin\theta-6\pi\mu Rr^2\dot{\theta}\\mr^2\ddot{\theta}=mgr\sin\theta-6\pi\mu Rr^2\dot{\theta}\ \ \ \Rightarrow\ \ \ \ddot{\theta}=\frac{g}{r}\sin\theta-\frac{6\pi\mu R}{m}\dot{\theta}This is the full equation of motion for a pendulum with linear air resistance (expressed in terms of the coordinate θ and its time derivatives).
As mentioned earlier, if you’re looking to have a deep understanding of Lagrangian mechanics, my book Lagrangian Mechanics For The Non-Physicist (link to the book page) is the perfect starting point for you. The best part is that you’ll get to learn everything from scratch as the book gradually builds upon each topic to eventually cover things like symmetries in physics and Noether’s theorem – beginning all the way from basic Newtonian mechanics.