Rope Sliding Down a Table With Friction (Step-By-Step Solution)
Physics, especially classical mechanics, is filled with tons of interesting problems. Possibly one of my favorites is the ‘rope sliding down a table’ -problem.
What makes this problem so interesting is that it can be solved using a few extremely elegant techniques. In this article, I’ll show you exactly how to do that.
Essentially, we are going to derive the equations of motion for a rope sliding down a table by using Lagrangian mechanics. To make the problem more interesting, we will also take into account friction. We will then solve the equations of motion using a few neat differential equation solving techniques.
This problem is a perfect example of how Lagrangian mechanics is used and how it’s possible to incorporate non-conservative forces into the Lagrangian formulation. The problem also makes for a great example of a technique called Laplace transform, which I’ll explain later.
Steps for solving the rope sliding down a table problem:
- Find the kinetic and potential energies.
You’ll need the kinetic and potential energies to find the Lagrangian of the rope. The key thing to note in this step is that the potential energy is actually time dependent.
- Construct the Lagrangian.
Once you have the kinetic and potential energies, construct the Lagrangian by using the formula L=T-U.
- Calculate the energy lost from friction.
Since friction can’t be directly incorporated into the Lagrangian of the rope, you’ll need to use a dissipation function to account for the energy lost due to friction.
- Write down the Euler-Lagrange equations.
Plug the Lagrangian you’ve constructed into the Euler-Lagrange equations. From this, you’ll get the equation of motion for the rope.
- Apply a Laplace transform to the equations of motion.
You’ll use the Laplace transform in order to actually solve the equation of motion and to get a function describing the motion of the rope.
- Apply the inverse Laplace transform.
In this step, you’ll need the inverse Laplace transform and some algebra to solve for the function describing the motion of the rope.
- Use the convolution theorem.
You can use the convolution theorem to turn a tricky part of the problem into a very simple integral. After this, you’ll have the final solution to the rope problem.
Although I’ll explain every step along the way in full detail, you may still want to read my introductory article on Lagrangian mechanics, if you’re not familiar with the formulation.
I also have a list of my favorite resources for self-studying Lagrangian mechanics (and classical mechanics in general) here.
You may also try this problem as an exercise on your own and if you get stuck on something, simply come back and read my explanations down below. Anyways, let’s get started!
Step-By-Step Derivation of The Equations of Motion
First of all, we have to go over what the problem is all about in a bit more detail.
The ‘rope sliding down a table’ -problem is a rope placed on the edge of a table, so that its other end is hanging off the table. Since gravity is pulling the hanging end of the rope downwards, it will begin to slide down the table and we’ll want to find the equations describing the sliding of this rope.
A picture of the situation can be seen down below with all of the information we’ll use. Essentially, we’re dividing the rope into two parts; the part hanging off the table and the part on top of the table.
We can describe the motion of this rope by simply specifying the length of the part of the rope that is hanging off the table at any given instant of time. This we’ll call x(t), which will be a function of time, of course.
Also, since we’re dividing the rope into two parts, we need to specify the mass of each of the parts separately. What makes this interesting is the fact that when the rope slides, the individual masses of each of the two parts will change with time (although the total mass of the rope does not!).
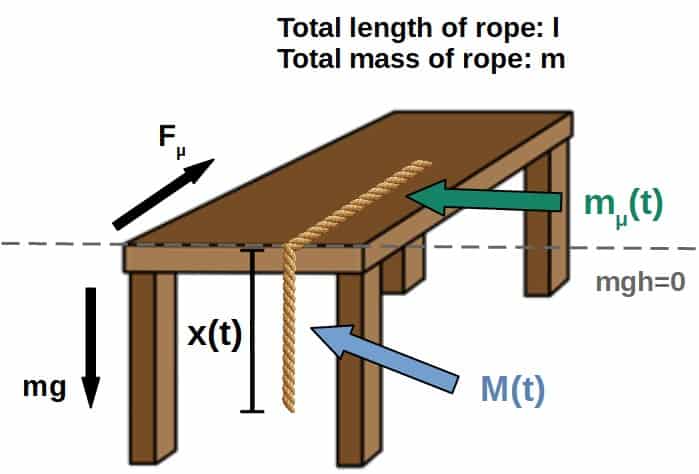
The masses of the two parts of the rope are functions of time since they are changing with time as the rope slides down the table. The total mass of the rope is m and the total length is little l. We’re assuming the rope to be at rest to begin with (i.e. it has zero initial velocity).
Now, we also have to go over a little bit of how we’ll solve this problem. Essentially, we just have to specify the total kinetic and potential energies of the rope and construct the Lagrangian, which is of the form:
L=T-UT here is denoting kinetic energy and U is potential energy.
Once we have the Lagrangian, we can plug it into the Euler-Lagrange equations (and specify our generalized coordinates). This, I’ll explain once we get to it.
Step 1: Find The Kinetic and Potential Energies
The first step is to specify the kinetic and potential energies of the rope.
The kinetic energy is easy. The total velocity of this rope is just the time derivative of the “position function”, dx(t)/dt. The part of the rope that’s on the table is also moving with this same velocity (otherwise there would be some weird stretching effects, which we’re assuming there aren’t).
The kinetic energy is therefore simply:
T=\frac{1}{2}m\dot x^2
For the rest of this article, I’m going to denote the time derivative of something by putting a dot above it, the second time derivative by two dots etc.
Now, the potential energy is a bit trickier. First of all, only the part hanging off the table has potential energy, the other part of the rope is just sitting on the table and its height is not changing (we’ve chosen the zero level of PE to be at the table).
So, the total potential energy of the rope is just the potential energy of this hanging part. Now, the key thing to realize is that the mass of the hanging part, M(t) (from the picture), is changing with time as the rope slides.
But what is this “mass function” M(t)? Let’s think of a simple example. If a third of the rope is hanging off the table, the mass of this part would be a third of the total mass m.
In other words, the mass of the part hanging off the table is the ratio of the length of this part (x) to the total length of the rope (l) multiplied by the total mass m:
M\left(t\right)=\frac{x\left(t\right)}{l}mBut the problem now is that the rope isn’t just some point mass, so what part exactly is the gravitational force targeted at?
If we assume that the mass is uniformly distributed across the rope, then all of the potential energy can be thought of as being at the center of mass, i.e. halfway across the hanging part of the rope (x(t)/2).
The potential energy is therefore (simply by using the formula U=mgh):
U=-M\left(t\right)g\frac{x\left(t\right)}{2}Note that since the zero level is at the table, the “height” of the center of mass is simply negative x(t)/2.
And inserting M(t) (I’m also going to stop writing x(t) and just write x):
U=-\frac{x}{l}mg\frac{x}{2}=-\frac{g}{l}m\frac{x^2}{2}Step 2: Construct The Lagrangian
Now that we have the kinetic and potential energies, we can construct the Lagrangian, which is just the difference of kinetic and potential energy:
L=T-U=\frac{1}{2}m\dot{x}^2-\left(-\frac{g}{l}m\frac{x^2}{2}\right)=\frac{1}{2}m\dot{x}^2+\frac{g}{l}m\frac{x^2}{2}Step 3: Calculate The Energy Lost From Friction (By Using a Dissipation Function)
The Lagrangian we derived earlier, however, doesn’t describe the friction exerted by the table when the rope begins to slide. Now, frictional forces are not so simple to deal with in Lagrangian mechanics, but it can certainly be done.
The way we’re going to do this is to basically calculate the energy lost from friction since the Lagrangian has to do with energies. We can then take this “lost” energy into account when writing down the Euler-Lagrange equations.
Now, how do we calculate the energy lost from friction? The answer is that we use something called the dissipation function, which essentially describes the rate of the dissipated (“lost”) energy due to a non-conservative force, such as friction.
The dissipation function (denoted by the letter D) is defined as follows:
D=\frac{1}{n+1}\sum_j^{ }c_jv_j^{n+1}
This formula is similar to the more conventionally used Rayleigh dissipation function, but this is more general as it allows for any powers of velocity as well as friction due to normal forces etc.
If you want to know what this formula actually means and how it describes the dissipated or “lost” energy due to friction, I explain all of that and a bunch of examples in this article.
Now, since we only have one coordinate we need to worry about (x), this summation is just a sum over one and we can get rid of it.
In this problem, we’re interested in the friction due to the normal force (i.e. the sliding friction). In this case, the n here will be n=0, since the friction force shouldn’t depend on the velocity, i.e. it’s proportional to the zeroth power of velocity (this is all explained in the article linked above).
Now, what is the friction force in this case? It is essentially just the kinetic friction generated by the surface of the table when the rope begins sliding. The usual formula for that is just:
F_{\mu}=\mu NN here is the normal force, perpendicular to the surface.
Since the part of the rope where the friction force is applying stays in contact with the table (i.e. it doesn’t have any vertical movement), the normal force has to be equal to the gravitational force downwards, which is:
N=m_{\mu}\left(t\right)gThe mµ(t) here is the mass of the part of the rope that is on the table (which of course changes with time as the rope slides off).
This mass term (mass of the rope on the table) here is simply the total mass (m) minus the mass that’s hanging off the table (M(t)). M(t) we already specified earlier, so this then becomes:
m_{\mu}\left(t\right)=m-M\left(t\right)=m-\frac{x}{l}m=m\left(1-\frac{x}{l}\right)So, we therefore get the friction force to be:
F_{\mu}=\mu gm\left(1-\frac{x}{l}\right)We can now calculate the dissipation function, which is quite simple. We already specified earlier that the dissipation function should have n=0, which means (also, the velocity is just x-dot)
D=\frac{1}{0+1}cv^{0+1}=cv=c\dot xNow we have to define this coefficient c in a meaningful way. The way to do this, would be, by looking at the friction force, like this:
c=\mu gm\left(1-\frac{x}{l}\right)
Note that the coefficient c is actually time-dependent here since the position x is also time-dependent.
The dissipation function is then:
D=\mu gm\left(1-\frac{x}{l}\right)\dot{x}So, we then have the dissipation function, which accounts for the dissipated energy due to friction. Next, I’ll show you what to actually do with it when we can finally obtain the equations of motion.
Step 4: Write Down The Euler-Lagrange Equations
The way we derive equations of motion in Lagrangian mechanics is by plugging the Lagrangian into a particular set of equations (we only have one of them in this problem) known as the Euler-Lagrange equations, which then spits out the equations of motion for the system:
\frac{d}{dt}\frac{\partial L}{\partial \dot q_i}=\frac{\partial L}{\partial q_i}
In our problem, we have defined the generalized coordinates as q=x.
There is just one catch here. We also have to add a term in these equations to account for the friction force. The way to do this is to add a term involving the dissipation function in the following way (also setting q=x):
\frac{d}{dt}\frac{\partial L}{\partial\dot x}=\frac{\partial L}{\partial x}-\frac{\partial D}{\partial\dot x}This form of the Euler-Lagrange equation is explained more in this article.
Now we just insert the Lagrangian and the dissipation function from earlier and get:
\frac{d}{dt}\frac{\partial}{\partial\dot{x}}\left(\frac{1}{2}m\dot{x}^2+\frac{g}{l}m\frac{x^2}{2}\right)=\frac{\partial}{\partial x}\left(\frac{1}{2}m\dot{x}^2+\frac{g}{l}m\frac{x^2}{2}\right)-\frac{\partial}{\partial\dot{x}}\left(\mu gm\left(1-\frac{x}{l}\right)\dot{x}\right)
To take partial derivatives like this, you just hold everything constant except the variable you’re differentiating with respect to (derivative of a constant is zero).
This is essentially the equation of motion for the rope system. We can cancel out the mass from both sides and write this a bit differently:
\ddot{x}=\frac{g}{l}x+\frac{g}{l}\mu x-\mu gEquation of motion:
\ddot{x}=\frac{g}{l}\left(1+\mu\right)x-\mu g
Here we have the finished equation of motion. Now, something like this isn’t all that useful, we would rather want to have the position (x) as a function of time. To get it, we have to solve this differential equation, which we’ll do next.
Step-By-Step Solution For The Equations of Motion
Here we will actually solve the above equation of motion for a function of time (x(t)) that describes the position of the rope in terms of the initial conditions. To do this, we’ll use a technique known as the Laplace transform.
Essentially, a Laplace transform is a mathematical tool for converting some function of time, f(t), into another function of a complex frequency s, F(s). The Laplace transform works especially well for problems in which the system is evolving to rest with time (such as is with this rope problem).
Now, for the sake of this problem, it doesn’t make sense to speak of a complex frequency. Instead, the Laplace transform will simply give us an elegant method for turning a differential equation into a simple algebraic problem.
Okay, but what does the Laplace transform actually do? Essentially, to take a Laplace transform of some function f(t), you calculate the following integral, which gives some new function F(s) (this is the definition of the Laplace transform):
\mathscr{L}\left\{f\left(t\right)\right\}=\int_0^{\infty}f\left(t\right)e^{-st}dt=F\left(s\right)Now, it might not be obvious yet how this helps at all in solving differential equations, but it will soon. There is just one more concept we need, which is the notion of an inverse Laplace transform.
An inverse Laplace transform is simply the inverse operation of the Laplace transform, which gives back the original function:
\mathscr{L}^{-1}\left\{F\left(s\right)\right\}=f\left(t\right)Down below I’ve made a table of all of the Laplace transform identities we’ll use and labeled each of them by a number, so that they are easy to refer back to (they can all essentially be proven by using the integral formula given above, but for practicality, I won’t prove them here).
Table of useful Laplace transform identities:
| Label (#) | f(t) | \xrightleftharpoons[\mathscr{L}^{-1}]{\mathscr{L}} | F(s) |
|---|---|---|---|
| 1 | f\left(t\right) | F\left(s\right) | |
| 2 | f''\left(t\right) | s^2F\left(s\right)-sf\left(0\right)-f'\left(0\right) | |
| 3 | a | \frac{a}{s} | |
| 4 | \cosh\left(at\right) | \frac{s}{s^2-a^2} | |
| 5 | \sinh\left(at\right) | \frac{a}{s^2-a^2} |
All of this may seem somewhat abstract right now, but when we get to using these, it all becomes so clear and I’ll explain each step of the way to the best of my ability.
Step 5: Apply a Laplace Transform To The Equations of Motion
The first thing we’ll do in solving this differential equation is going to be simply applying the Laplace transform. This, you’ll see will give us a sweet and elegant way of turning the differential equation into a fairly simple algebraic one.
So, applying the Laplace transform on each term of our equation of motion, we have (the Laplace transform is a linear operator, so it can be applied to each term separately):
\mathscr{L}\left\{\ddot{x}\right\}=\mathscr{L}\left\{\frac{g}{l}\left(1+\mu\right)x\right\}-\mathscr{L}\left\{\mu g\right\}By linearity of the Laplace transform, we can pull out the constants to make it a bit more clear (just like how you can pull out constants in derivatives, for example):
\mathscr{L}\left\{\ddot{x}\right\}=\frac{g}{l}\left(1+\mu\right)\mathscr{L}\left\{x\right\}-\mathscr{L}\left\{\mu g\right\}Now, here comes the interesting part, which is actually taking the Laplace transforms.
On the left hand side, we have the Laplace transform of the second derivative of a function, which is identity #2 on our table from earlier! (just replace f(t) with x(t))
On the right hand side, we have the Laplace transform of simply a function of t, which is just identity #1 as well as the Laplace transform of a constant (µg), which is identity #3.
So, all in all from applying the Laplace transforms, we get:
s^2X\left(s\right)-sx\left(0\right)-\dot{x}\left(0\right)=\frac{g}{l}\left(1+\mu\right)X\left(s\right)-\frac{\mu g}{s}Now, let’s think about our initial conditions. The initial velocity is zero since we’re assuming the rope to be at rest at the beginning (at t=0). So, the third term here is just zero.
This x(0) term is also just an initial condition, which is just the length of the rope hanging off the table to begin with (this we’ll call x0). We can also do a few simplifications:
s^2X\left(s\right)-sx_0=\frac{g}{l}\left(1+\mu\right)X\left(s\right)-\frac{\mu g}{s} s^2X\left(s\right)-\frac{g}{l}\left(1+\mu\right)X\left(s\right)=sx_0-\frac{\mu g}{s} \left(s^2-\frac{g}{l}\left(1+\mu\right)\right)X\left(s\right)=sx_0-\frac{\mu g}{s}To make our calculations a bit nicer looking, we will call this one term (which is just a bunch of constants) c:
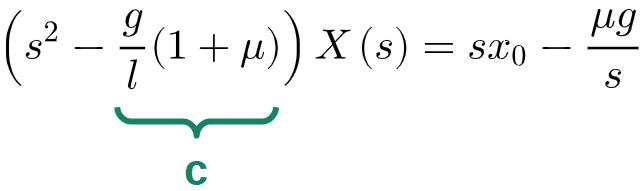
We’ll also want to isolate this X(s) function, which will ultimately give us the solution (you’ll see why soon!). So, let’s divide both sides by (s2-c) to get:
X\left(s\right)=\frac{sx_0}{s^2-c}-\frac{\mu g}{s\left(s^2-c\right)}Do you see what we just did here? Essentially, we’ve just turned the differential equation into some function equal to a bunch of initial conditions and other constants. This is exactly the form we’d like our solution to have.
Now, we’d actually rather prefer something with x(t) instead of this X(s) thing. This is where the inverse Laplace transform comes into play.
Step 6: Apply The Inverse Laplace Transform
The key to this problem is using the Laplace transform in order to get the function X(s) alone and then apply the inverse Laplace transform, which will simply give back the original function x(t).
From the inverse Laplace transform we have:
\mathscr{L}^{-1}\left\{X\left(s\right)\right\}=\mathscr{L}^{-1}\left\{\frac{sx_0}{s^2-c}\right\}-\mathscr{L}^{-1}\left\{\frac{\mu g}{s\left(s^2-c\right)}\right\}The left-hand side is obviously just going to give back x(t):
x\left(t\right)=\mathscr{L}^{-1}\left\{\frac{sx_0}{s^2-c}\right\}-\mathscr{L}^{-1}\left\{\frac{\mu g}{s\left(s^2-c\right)}\right\}Now, it’s these terms on the right-hand side, which require a bit of work to solve, but it’s not too hard.
Let’s look at the first term. By linearity of the Laplace transform, we can pull out x0 since it’s just a constant:
\mathscr{L}^{-1}\left\{\frac{sx_0}{s^2-c}\right\}=x_0\mathscr{L}^{-1}\left\{\frac{s}{s^2-c}\right\}This thing actually looks a whole lot like identity #4 from the Laplace transform table shown earlier. In fact, it is exactly that if we express it in the following form:
x_0\mathscr{L}^{-1}\left\{\frac{s}{s^2-c}\right\}=x_0\mathscr{L}^{-1}\left\{\frac{s}{s^2-\left(\sqrt{c}\right)^2}\right\}Now this thing in the parentheses is nothing but the Laplace transform of cosh(at) with a being the same as the square root of c. So, form this inverse Laplace transform term, we just get back the hyperbolic cosine function:
x_0\mathscr{L}^{-1}\left\{\frac{s}{s^2-\left(\sqrt{c}\right)^2}\right\}=x_0\cosh\left(\sqrt{c}t\right)This term is then finished. Let’s now look at the other inverse Laplace transform term from our equation earlier. We can express it in the following form:
\mathscr{L}^{-1}\left\{\frac{\mu g}{s\left(s^2-c\right)}\right\}=\mathscr{L}^{-1}\left\{\frac{\mu g}{s}\frac{1}{s^2-\left(\sqrt{c}\right)^2}\right\}This is again starting to look similar to what we just did with the previous inverse Laplace transform. It is just missing an s from the numerator.
But, since s is a variable and not a constant, we can’t simply multiply by s on the inside of these parentheses and divide by s on the outside.
What we can do, however, is multiply and divide by any constant (since constants can be pulled outside the operator if we wish to). In this case, the constant should be the square root of c:
\mathscr{L}^{-1}\left\{\frac{\mu g}{s}\frac{1}{s^2-\left(\sqrt{c}\right)^2}\right\}=\frac{1}{\sqrt{c}}\mathscr{L}^{-1}\left\{\frac{\mu g}{s}\frac{\sqrt{c}}{s^2-\left(\sqrt{c}\right)^2}\right\}But what does this resemble? It’s exactly the product of the identities #3 and #5! Now, it’s tempting to just say that maybe we could distribute the Laplace transform to both of these terms in the product separately.
Unfortunately, Laplace transforms don’t work quite this way. Just like how there is a special rule for the derivative of a product (known as the product rule), there is a rule for the Laplace (and inverse Laplace) transform of a product. This is known as the convolution theorem and it will be our final step in solving this problem.
Step 7: Use The Convolution Theorem To Obtain The Final Solution
At this point, we’re almost finished with the solution of this problem. There is just one key theorem we need to take advantage of, which is the convolution theorem for Laplace transforms.
Essentially, convolution is a way to separate otherwise very difficult or impossible Laplace transforms (which have the form of the product of two Laplace transforms) into quite simple integrals.
Here’s a useful video explaining the convolution theorem very well if you wish to watch it:
Now, without getting into proofs or details about the convolution theorem too much, one way to mathematically state it is:
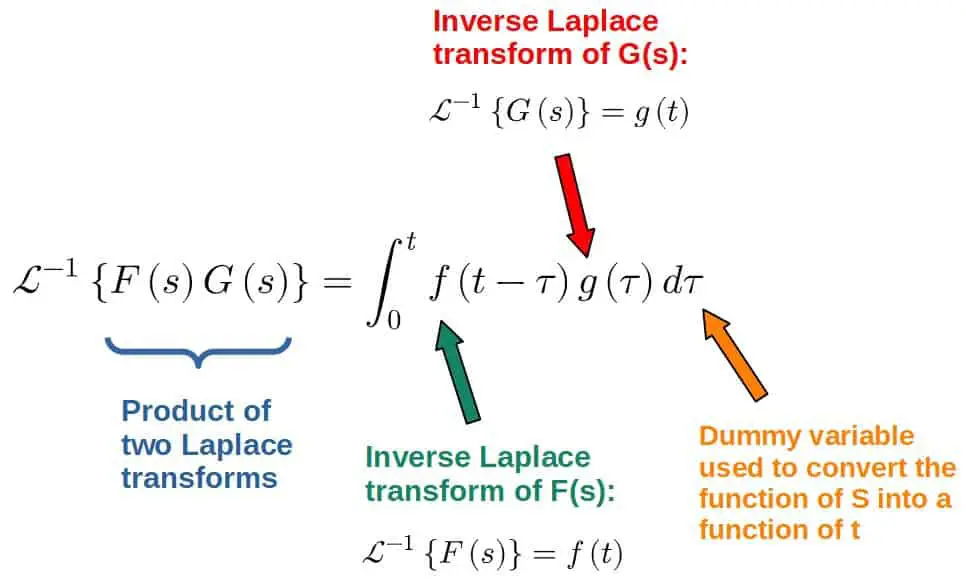
In our problem, these would be:
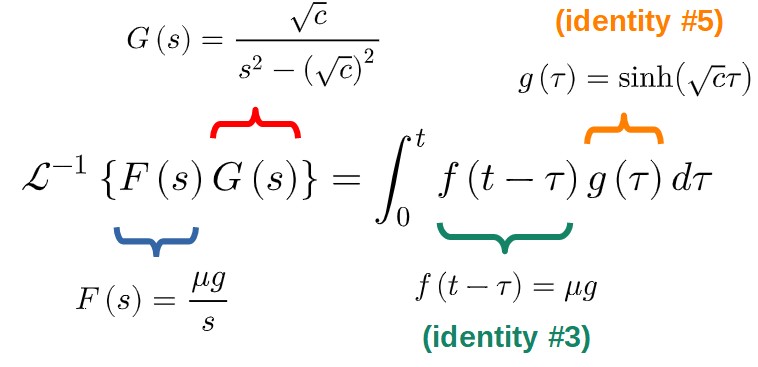
Essentially what we’ve done now is converted this inverse Laplace transform into a simple integral:
\frac{1}{\sqrt{c}}\mathscr{L}^{-1}\left\{\frac{\mu g}{s}\frac{\sqrt{c}}{s^2-\left(\sqrt{c}\right)^2}\right\}=\frac{\mu g}{\sqrt{c}}\int_0^t\sinh\left(\sqrt{c}\tau\right)d\tauAll we need here is to basically just calculate the integral of the hyperbolic sine function, which is nothing but the hyperbolic cosine:
\frac{\mu g}{\sqrt{c}}\int_0^t\sinh\left(\sqrt{c}\tau\right)d\tau=\frac{\mu g}{\sqrt{c}}\bigg/_{\!\!\!\!\!0}^t\frac{1}{\sqrt{c}}\cosh\left(\sqrt{c}\tau\right)Substituting the integration limits, we get (and using the fact that cosh(0)=1):
\frac{\mu g}{\sqrt{c}}\bigg/_{\!\!\!\!\!0}^t\frac{1}{\sqrt{c}}\cosh\left(\sqrt{c}\tau\right)=\frac{\mu g}{c}\left(\cosh\left(\sqrt{c}t\right)-1\right)Now we have everything we need to construct the solution. Recall what we originally had:
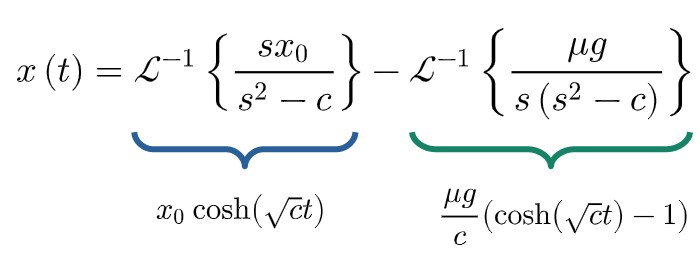
And that’s it. We’re done now! Here we have the solution to our equation of motion. All we have to do now is substitute back the constant c and write this in little nicer form:
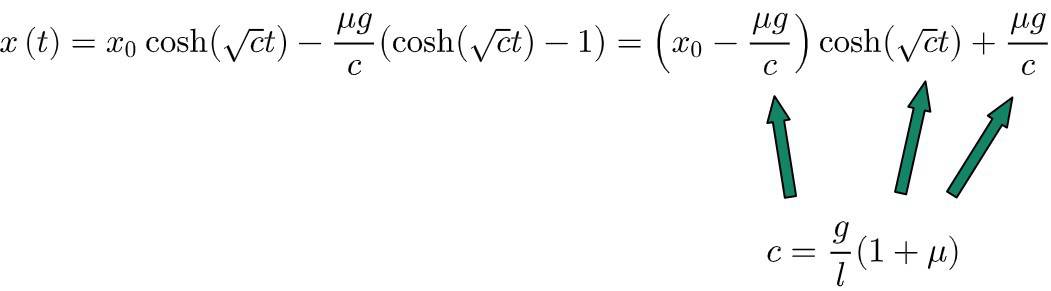
Solution to the equation of motion:
x\left(t\right)=\left(x_0-\frac{\mu}{1+\mu}l\right)\cosh\left(\sqrt{\frac{g}{l}\left(1+\mu\right)}t\right)+\frac{\mu}{1+\mu}l
This equation tells us how much of the rope is hanging off the table at any given time in terms of the initial conditions and parameters. We can also use this to find information about anything we wish to.
For example, we could find the time it takes for the rope to completely fall off the table by plugging in x(t) = l (at that point, the whole length l of the rope is hanging off the table, i.e. it has fallen off) and then solve for the sliding time:
t_s=\sqrt{\frac{l}{g}\left(1+\mu\right)}\cosh^{-1}\left(\frac{1-\frac{\mu}{1+\mu}}{\frac{x_0}{l}-\frac{\mu}{1+\mu}}\right)If you’re interested in more classical mechanics stuff, I’d recommend reading my article comparing Lagrangian to Newtonian mechanics. In there, I show plenty of cool examples to illustrate how the two formulations differ from one another.